
Trắc nghiệm tổng hợp Toán 12 - 200 bài trắc nghiệm nguyên hàm và tích phân (cơ bản đến nâng cao)
Từ khoá: trắc nghiệm Toán 12 nguyên hàm tích phân Toán lớp 12 luyện thi THPT bài tập tích phân ôn thi đại học câu hỏi nâng cao công thức nguyên hàm đáp án chi tiết
Số câu hỏi: 224 câuSố mã đề: 9 đềThời gian: 1 giờ
160,392 lượt xem 12,333 lượt làm bài
Xem trước nội dung:
Tính thể tích vật thể tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đường elip có phương trình quay xung quanh trục Ox.
Tính thể tích của vật thể giới hạn bởi hai mặt phẳng Biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm có hoành độ là một tam giác vuông cân có cạnh huyền bằng sinx+2
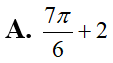
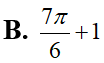
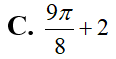

Họ nguyên hàm của hàm số là
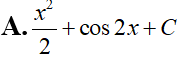
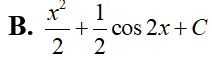
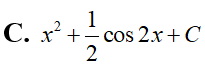
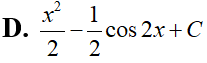
Nếu thì giá trị của a + 2b là
Nếu thì a+2b+3c là
Họ nguyên hàm của hàm số là
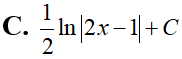
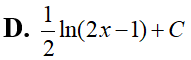
Cho hàm số f(x) liên tục trên [0;3] và Tính
Cho hàm số có đạo hàm liên tục trên khoảng Khi đó bằng
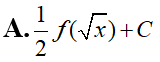
Biết với a, b, c là các số hữu tỉ. Tính P = a + b + c.
Cho H là hình phẳng giới hạn bởi parabol , tiếp tuyến với (P) tại M(2;4) và trục hoành. Tính diện tích của hình phẳng (H)?
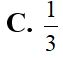
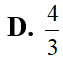
Cho hình trụ có trục OO', bán kính đáy r và chiều cao Hai điểm M, N di động trên đường tròn đáy (O) sao cho OMN là tam giác đều. Gọi H là hình chiếu vuông góc của O trên mặt phẳng (O’MN). Khi M, N di động trên đường tròn (O) thì đoạn thẳng OH tạo thành mặt xung quanh của một hình nón, tính diện tích S của mặt này
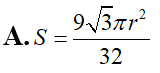
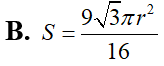
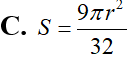
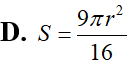
Trong không gian (Oxyz), cho vật thể (H) giới hạn bởi hai mặt phẳng có phương trình x=a và x=b (b>a) Gọi S(x) là diện tích thiết diện của (H) bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x, với Giả sử hàm số y=S(x) liên tục trên đoạn [a;b]. Khi đó, thể tích V của vật thể (H) được cho bởi công thức:
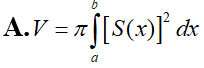
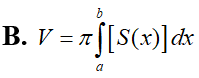
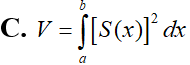
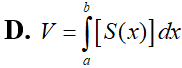
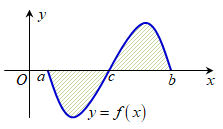
Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số = trục hoành và đường thẳng x=a;x=b (như hình vẽ bên). Hỏi khẳng định nào dưới đây là khẳng định đúng?

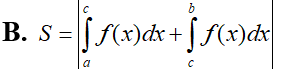
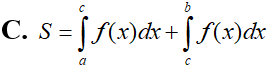
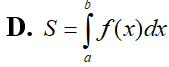
Cho hàm là hàm liên tục thỏa mãn . Tính

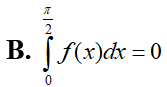
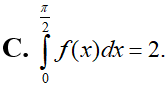

Cho hàm số liên tục có đồ thị như hình bên dưới. Biết và Tính F(2)-F(-5).
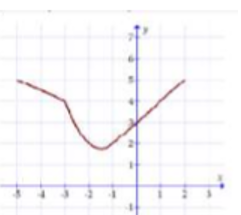
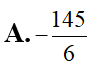
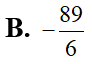
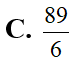
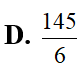
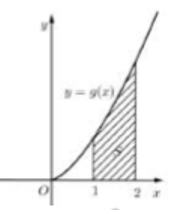
Cho hàm số liên tục trên R và hàm số có đồ thị trên đoạn [0;2] như hình vẽ. Biết diện tích miền tô màu là tính tích phân
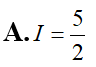
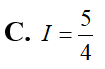
Cho đồ thị Gọi M là điểm thuộc (C), A(9;0). Gọi S1 là diện tích hình phẳng giứi hạn bởi (C), đường thẳng x = 9 và trục hoành; S2 là diện tích tam giác OMA. Tọa độ điểm M để S1 = 2S2 là:
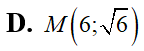
Nếu thì là:
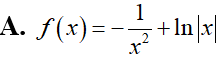
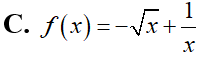
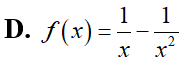
Cho . Tính
Tìm một nguyên hàm F(x) của hàm số
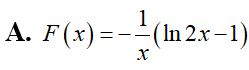
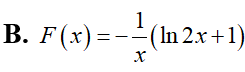
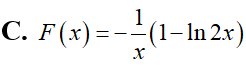
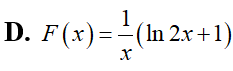
Cho đồ thị hàm số y=f(x) Diện tích hình phẳng (phần có dấu gạch trong hình) là
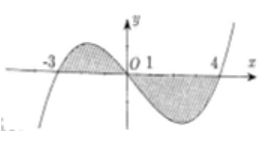
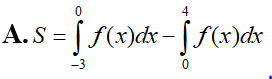
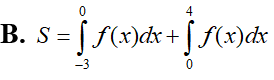
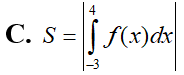
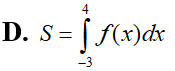
Biết với a, b. c là số nguyên. Tính P = 2a + b.
Hàm số nào sau đây là một nguyên hàm của hàm số ?
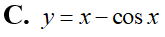
Tích phân bằng
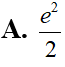
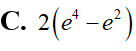
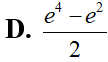
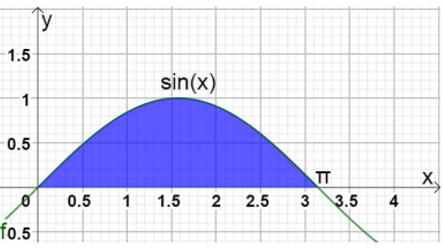
Cho hình (H) trong hình vẽ bên dưới quay quanh trục Ox tạo thành một khối tròn xoay có thể tích bằng bao nhiêu?
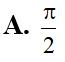
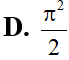
Đề thi tương tự
97 mã đề 7881 câu hỏi 1 giờ
172,186 xem13,239 thi
3 mã đề 102 câu hỏi 1 giờ
155,011 xem11,907 thi
1 mã đề 21 câu hỏi 1 giờ
154,954 xem11,912 thi
4 mã đề 66 câu hỏi 1 giờ
190,864 xem14,674 thi
4 mã đề 65 câu hỏi 1 giờ
163,147 xem12,542 thi
3 mã đề 66 câu hỏi 1 giờ
170,769 xem13,129 thi
4 mã đề 65 câu hỏi 1 giờ
153,521 xem11,797 thi
