By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Tìm vị trí của điểm M để hình thang ABDC có chu vi nhỏ nhất.

Rút gọn phân thức: $\frac{{\text{x}}^{\text{3}}{\text{ + y}}^{\text{3}}{\text{ + z}}^{\text{3}}\text{ - 3xyz}}{{\left(\text{x - y}\right)}^{\text{2}}\text{ + }{\left(\text{y - z}\right)}^{\text{2}}\text{ + }{\left(\text{z - x}\right)}^{\text{2}}}$

Tìm các chữ số a, b, c, d sao cho tổng abc + dba chia hết cho aa và được thương là aa (abc, dba là các số có 3 chữ số theo thứ tự là a, b, c và d, b, a; aa là số có 2 chữ số đều bằng a).

Giải phương trình : x⁴ - 8x² + x + 12 = 0

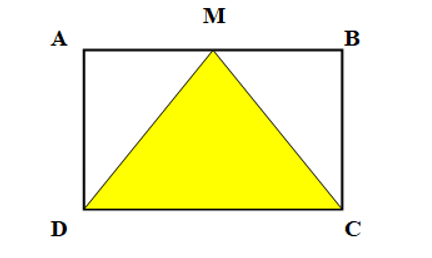
Cho hình chữ nhật ABCD có chiều dài 6 cm, chiều rộng 4 cm (như hình vẽ). Diện tích hình tam giác MDC bên trong hình chữ nhật là bao nhiêu?

Cho $\Delta ABC$ vuông tại A có đường cao AH. Biết AC = 15cm; HB = 16cm. Tính BC; AB; AH; CH

Hai vòi nước cùng chảy vào một bể. Nếu chảy một mình thì vòi I chảy đầy bể trong 10 giờ, vòi II chảy đầy bể trong 15 giờ. Còn vòi thứ ba được lắp sát đáy bể để tháo nước từ bể ra. Nếu bể đang đầy thì vòi thứ ba tháo hết nước ra trong 30 giờ. Trong bể đã có 4 1 bể nước, người ta mở cho vòi I và vòi II chảy trong 3 giờ rồi mở tiếp vòi thứ ba. Hỏi sau khi mở vòi thứ ba thì sau bao lâu bể nước đầy?

Ba vòi nước 1, 2, 3 .Nếu chảy một mình vào một bể cạn thì chảy đầy bể theo thứ tự 4 giờ, 6 giờ, 9 giờ. Lúc đầu người ta mở hai vòi 1 và 2 trong 1 giờ 30 phút, sau đó đóng vòi 1 rồi mở tiếp vòi 3 cùng chảy với vòi 2 cho đến khi đầy bể. Hỏi vòi chảy trong bao lâu?

Cho một số có hai chữ số, khi ta viết thêm vào bên trái số đó một chữ số 1 thì tổng của số mới và số đã cho là 168 . Tìm số đã cho.

Cho đa thức: f(x) = x⁴ + ax³ + bx² + cx + d ( với a, b, c, d là các số thực). Biết f(1) = 10; f(2) = 20; f(3) = 30. Tính giá trị của biểu thức: A = f(9) + f(-5)

Tìm 4 số lập thành một CSN biết tổng bốn số bằng 15 và tổng các bình phương của chúng bằng 85

Tính  $\text{P = }\frac{\frac{\text{1}}{\text{2}}\text{ + }\frac{\text{1}}{\text{3}}\text{ + }\frac{\text{1}}{\text{4}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2012}}}{\frac{\text{2011}}{\text{1}}\text{ + }\frac{\text{2010}}{\text{2}}\text{ + }\frac{\text{2009}}{\text{3}}\text{ + }\mathrm{...}\text{ + }\frac{\text{1}}{\text{2011}}}$

Tìm x biết 135 - 5(x + 4) = 35

Có 4 đội bóng đá thi đấu vòng tròn( hai đội bất kì đều gặp nhau một trận)

a) Hỏi có bao nhiêu trận.

b) Câu hỏi với n đội bóng thi đấu vòng tròn thì có tất cả bao nhiêu trận

Trong 1 bảng đấu loại bóng đá có 4 đội thi đấu vòng tròn 1 lượt đội thắng được 3 điểm, đội hòa được 1 điểm, đội thua được 0 điểm. Tổng số điểm của 4 đội khi kết thúc bảng đấu là 16 điểm. Tính số trận hòa.

Cho tam giác ABC có AB = 2, AC = 3, $\widehat{\text{BAC}}\text{ = 60°}$. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn  $\overrightarrow{\text{AD}}\text{ = }\frac{\text{7}}{\text{12}}\overrightarrow{\text{AC}}$

a) Tính  $\overrightarrow{\text{AB}}\text{ . }\overrightarrow{\text{AC}}$

b) Biểu diễn $\overrightarrow{\text{AM}}\text{, }\overrightarrow{\text{BD}}$ theo  $\overrightarrow{\text{AB}}\text{ , }\overrightarrow{\text{AC}}$

c) Chứng minh  $AM\perp BD$

Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) : y = (m - 3)x + 1 $\left(\text{m }\ne \text{3}\right)$bằng $\frac{1}{2}$

Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

Cho một đường thẳng d và hai điểm phân biệt A, B không thuộc d.

Tìm điểm C thuộc d sao cho A, B, C thẳng hàng. Khi nào không thể tìm được điểm C như vậy?

Hưởng ứng phong trào quyên góp sách giáo khoa cũ giúp đỡ học sinh có hoàn cảnh khó khắn, ba lớp 7A, 7B, 7C đã quyên góp số sách lần lượt với tỉ lệ 3; 4; 5. Tính số sách giáo khoa của mỗi lớp quyên góp, biết số sách quyên góp của lớp 7C hơn lớp 7A là 22 quyển.

Cho biết $\frac{\text{x}}{\text{y}}\text{ = }\frac{\text{7}}{\text{10}}\text{ ; }\frac{\text{y}}{\text{z }}\text{ = }\frac{\text{10 }}{\text{13 }}$ và x + y + z =120 .Tìm x,y,z

Chứng minh đẳng thức : tan²x - sin²x = tan²x . sin²x

Cho hàm số y = -x + 5 có đồ thị là (d₁)  $y=\frac{x}{2}-1$  có đồ thị là (d₂)

A) vẽ (d₁), (d₂) trên cùng mặt phẳng tọa độ
B) tìm tọa độ giao điểm của (d₁), (d₂)

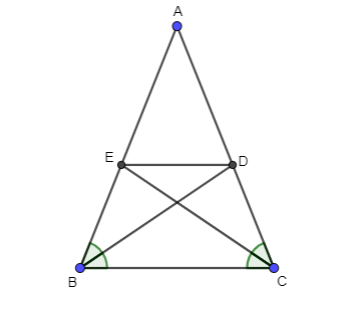
Cho $\Delta ABC$ cân tại A . Tia giác góc B cắt cạnh AC tại D, tia phân giác góc C cắt cạnh AB tại E. Chứng minh $\Delta ADE$ cân.

Cho $\Delta ABC$ vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.

a) Chứng minh BE = CD, AD = AE.

b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh $\Delta MAC$ vuông cân.

c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.

Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.

a) Chứng minh  $\text{ΔABH = ΔACH}$

b) Chứng minh AH ⊥ BC

c) Vẽ $\text{HD }\perp \text{AB (D }\in \text{AB)}$ và $HE\perp AC(E\in AC)$. Chứng minh: DE // BC

Cho $\text{ΔABC}$ có AB = AC. Tia phân giác của góc A cắt BC tại D.

a) Chứng minh tam giác ABD bằng tam giác ADC.

b) Kẻ $DH\perp AB$ (h tập hợp AB ) $DK\perp AC$ ( $K\in AC$) Chứng minh BH = CK.

c) Biết $\widehat{A}\text{=4}\hat{B}$ tính số đo các góc của tam giác  $\text{ΔABC}$

Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA

a) Cm: APBC là hình bình hành và BCDP là hình thang vuông

b) CM: 2Sbcdp = 3Sapbc          

c) Gọi N là trung điểm BC, Q là giao điểm DN và CM. Cm: AQ = AB

Cho $\Delta ABC$ cân tại A.Trên cạnh AB lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho AM + AN = 2AB.

a) Chứng minh rằng: BM = CN

b) Chứng minh rằng: BC đi qua trung điểm của đoạn thẳng MN.

c) Đường trung trực của MN và tia phân giác của $\widehat{BAC}$  cắt nhau tại K. Chứng minh rằng $\text{ΔBKM = ΔCKN}$ từ đó suy ra KC vuông góc với AN

Tính bằng cách thuận tiện nhất 
34 000 : 125 : 8 

Tính:

372,95 : 3                     757,5 : 35                     431,25:125                   35,1 x 8,5

Phân tích thành nhân tử c. 5(x + 3y) - 15x ( x + 3y )

Cho $∆$ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là các điểm đối xứng của H qua các cạnh AB, AC.

a) Chứng minh A, E, D thẳng hàng và BCED là hình thang.

b) Chứng minh $\text{BD . CE = }\frac{{\text{DE}}^{\text{2}}}{\text{4}}$.

c) Cho biết AB = 3cm, AC = 4cm. Tính DE và diện tích $∆$DHE.

Cho tam giác ABC có AB = 3; AC = 5; $\widehat{BAC}=60°.$Gọi M là điểm thuộc đoạn BC sao cho BM = 2MC . Tính độ dài đoạn AM.

Số lớn nhất có 4 chữ số khác nhau và tích các chữ số bằng 24 là ………

Giải phương trình:  $\text{x + }\frac{x}{\sqrt{{\text{x}}^{\text{2}}\text{-1}}}\text{ = }\frac{\text{35}}{\text{12}}$

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo AC và BD của hình bình hành ABCD.

a) Xác định giao tuyến của hai mặt phẳng (SBD) và (SAC).

b) Gọi K là trung điểm của SD. Tìm giao điểm G của BK với mặt phẳng (SAC); hãy cho biết tính chất của điểm G.

Cho hình thang vuông ABCD có $\widehat{\text{A}}\text{ =}\widehat{\text{ D }}{\text{= 90}}^{\text{0}}\text{; AB = AD = }\frac{\text{1}}{\text{2}}\text{CD}$. Gọi E là trung điểm của CD

a/ Tứ giác ABCE là hình gì?

b/ Tứ giác ABED là hình gì?

c/ Gọi M là giao điểm của AC và BE, K là giao điểm của AE và DM, O là giao điểm hai đuờng chéo hình vuông ABED. Kẻ DH vuông góc với AC cắt AE tại I. Chứng minh DB là tia phân giác của  $\widehat{IDK}$

d/ Chứng minh BIDK là hình thoi

Cho $∆$ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Cho $∆$ABC vuông tại A; đường phân giác BE. Kẻ EH $\perp$ BC (H ∈ BC). Gọi K là giao điểm của AB và HE. Chứng minh rằng:

a) ΔABE = ΔHBE.

b) BE là đường trung trực của đoạn thẳng AH.

c) EK = EC.    

d) AE < EC.

Cho $\Delta ABC$ vuông tại A điểm M thuộc cạnh BC từ M vẽ các đường thẳng vuông góc với AB ở D vuông góc với AC ở E

a) cm AM = BE.

b) gọi l là điểm đx của D qua A và K là điểm đx của E qua M cm IK, DE, AM đồng quy hai trung điểm O của mỗi đoạn.

c) gọi AH là đường cao của $\Delta ABC$tính số đo $\widehat{DHE}$.

Cho tứ giác ABCD có AC cắt BD tại O, $\widehat{ABD}=\widehat{ACD}$. Gọi E là giao điểm của AD và BC CMR :

a) các tam giác AOB và DOC đồng dạng.

b) Các tam giác AOD và BOC đồng dạng.

c) EA . ED = EB . EC.

Cho đường tròn (O) đường kính AB. Vẽ tiếp tuyến Ax, với đường tròn (O) (A là tiếp điểm ). Qua C thuộc tia Ax, vẽ đường thẳng cắt đường tròn (O) tại hai điểm D và E (D nằm giữa C và E; D và E nằm về hai phía của đường thẳng AB). Từ O vẽ OH vuông góc với đoạn thẳng DE tại H.

a) Chứng minh : tứ giác AOHC nội tiếp.

b) Chứng minh : AC . AE = AD . CE

c) Đường thẳng CO cắt tia BD, tia BE lần lượt tại M và N. Chứng minh : AM // BN

Chọn ngẫu nhiên 5 quân bài trong cỗ bài tú lơ khơ ta được một xấp bài. Tính xác suất để trong xấp bài này chứa hai bộ đôi (tức là có hai con cùng thuộc một bộ, hai con thuộc bộ thứ 2, con thứ 5 thuộc bộ khác).

Tổng của 2 số bằng 10,45. Tìm hai số đó, biết rằng nếu số hạng thứ nhất cộng với 4 lần số hạng thứ hai thì được 22,45.

Xác định hàm số bậc 2: y =  - 4x + c, biết rằng đồ thị của nó: 

a, Đi qua 2 điểm A (1; 2) và B (2;3)

b, Có đỉnh I (-2;-1)

c, Có hoành độ là -3 và đi qua điểm P (-2;1)

d, Có trục đối xứng là đường thẳng x= 2 và cắt trục hoành tại điểm M (3;0)

Cho $∆$ABC cân tại A ( $\widehat{A}<{90}^{\circ }$). Vẽ BH $\perp$ AC, CK $\perp$AB.

a) Chứng minh rằng AH = AK.

b) Gọi I là giao điểm của BH và CK. Chứng minh BIC cân.

c) Chứng minh HI là tia phân giác của A

Cho $∆$ABC, lấy điểm M thuộc cạnh AB sao cho $BM=\frac{1}{3}BA$.Gọi N là trung điểm của cạnh BC. Tính tỉ số   $\frac{SBMN}{SABC}$