Tổng hợp 20 đề thi thử THPT quốc gia môn Toán cực hay có lời giải chi tiết

Để đồ thị hàm số $$ y = ( x + 1 ) 2 ( x - m )  có dạng như hình bên thì giá trị m là

Cho hàm số  $$ y = x 4 + 1 . Khẳng định nào sau đây là sai

Số đường tiệm cận của đồ thị hàm số $$ y = x + 1 x 2 - a   ( 0 < a ≠ 1 )  là

Nghiệm của phương trình $$ log 2 ( x 2 - 1 ) = 3  là

Đạo hàm của hàm số  $$ y = log 9 ( x 2 + 1 ) là

Biết $$ ∫ 1 2 f ( x ) d x = 3 ,   ∫ 1 3 f ( x ) d x = 2 . Khi đó $$ ∫ 2 3 f ( x ) d x  bằng

Nguyên hàm của hàm số $$ f ( x ) = 2 x 3 - sin a  với a là tham số

Cho số phức z = 4 + 2i. Phần thực và phần ảo của w = 2z - i là

Cho lăng trụ đứng ABC.A'B'C' có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABC.A'B'C' là

Trong không gian hệ tọa độ Oxyz, cho mặt phẳng (P): = x-2y+3z-6=0. Vectơ chỉ phương của đường thẳng d vuông góc với (P) là

Trong hệ tọa độ Oxyz, phương trình nào sau đây không phải là phương trình đường thẳng Ox

Trong hệ tọa độ Oxyz , cho hai mặt phẳng (P)=x+2y+2z+11=0 và  (Q): x+2y+2z+2=0. Khoảng cách giữa (P) và (Q) là

Có 3 học sinh nữ và 2 học sinh nam.Hỏi có bao nhiêu cách sắp xếp các học sinh vào một bàn dài có 5 ghế ngồi

Giá trị của $$ l i m ( n + 2018 - n - 2018 )  là

Cho hàm số y=f(x) xác định, liên tục trên R và có bảng biến thiên sau.

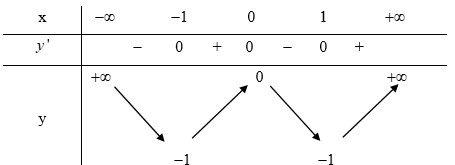
Tập hợp các giá trị m để phương trình f(x)=m+2 có hai nghiệm phân biệt là

Hàm số $$ y = x 3 - x 2 - 5  đạt cực đại tại

Giá trị lớn nhất của hàm số $$ y = x + 3 2 - x  trên đoạn $$ - 1 ; 1  là

Tập xác định của hàm số  $$ y = x - 2 ln ( x 2 - 5 x + 4 ) là

Cho x, y>0 và $$ x 2 + y 2 = 2 . Giá trị lớn nhất của biểu thức $$ A = 2 x y bằng

Cho I= $$ ∫ 0 1 f ( 2 x + 3 ) d x = 4 . Khi đó giá trị của $$ ∫ 3 5 f ( x ) d x  bằng

Cho số phức z=1+4i. Tổng bình phương các giá trị a để $$ z + a 2 - 2 i ¯ = 3 - 2 i  là

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. gọi M, N lần lượt là trung điểm của AB, AD. Gỉả sử $$ C N ∩ D M = H . Biết SH=2a và vuông góc với mặt phẳng  (ABCD). Khi đó thể tích S.CDMN

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B.   $$ A B = 3 a ;   B C = a 2 , mặt bên (A'BC) hợp với mặt đáy (ABC) một góc $$ 60 ° . Tính thể tích khối lăng trụ

Cho tam giác ABC vuông tại A có AB=5, $$ A B C = 30 ° . Hình cầu tạo bởi đường tròn ngoại tiếp tam giác ABC quay quanh BC có diện tích là

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $$ d : x - 1 2 = y + 1 3 = z - 1 - 1  và mặt phẳng $$ ( P ) :   x + 2 y - 2 z = 0 . Phương trình mặt cầu (S) có tâm I $$ ∈ d, tiếp xúc và cách (P) một khoảng bằng 1

Hộp A chứa 3 bi đỏ và 5 bi xanh; Hộp B đựng 2 bi đỏ và 3 bi xanh. Thảy một con xúc sắc; Nếu được 1 hay 6 thì lấy 1 bi từ hộp A. Nếu được số khác thì lấy từ hộp B. Xác suất để được một viên bi xanh là

Trong một trường học, có tổ Toán gồm 15 giáo viên trong đó có 8 giáo viên nam, 7 giáo viên nữ; tổ Lý gồm 12 giáo viên trong đó có 5 giáo viên nam, 7 giáo viên nữ. Chọn ngẫu nhiên mỗi tổ 2 giáo viên tham gia biên soạn đề thi THPT quốc gia. Tính xác suất sao cho trong các giáo viên được chọn có 2 nam và 2 nữ

Cho hàm số $$ y = 2 3 x 3 + ( m + 1 ) 2 + ( m 2 + 4 m + 3 ) x  đạt cực trị tại $$ x 1 ,   x 2 . Giá trị lớn nhất của biểu thức $$ A = x 1 x 2 - 2 ( x 1 + x 2 )  bằng

Biết đồ thị hàm số $$ y = x 4 - ( m 2 + 1 ) x 2 - 2 m + 3   ( C m ) . Giá trị của tham số m thỏa mãn $$ ( C m ) ∩ O x tại 4 điểm phân biệt lập thành cấp số cộng là

Cho hàm số $$ y =   a x + 1 b x - 3 , biết tiếp tuyến của đồ thị tại M song song với đường thẳng  -7x-y+2=0. Với M là đỉnh của $$ ( P ) :   x 2 - 8 x + 25 . Khi đó a+b bằng

Tổng số giá trị nguyên của m để phương trình $$ x 3 + x ( x + 1 ) = m ( x ² + 1 ) 2  có nghiệm thực là

Để bất phương trình $$ 16 x - 4 x + 1 - m > 0  có 2 nghiệm trái dấu thì số giá trị nguyên của m thỏa mãn là

Cho hàm số $$ y = x 2 = 5 x + 7   ( C 1 ) , $$ y = x + k   ( C 2 ) , gọi H là hình phẳng giới hạn bới  ( $$ C 1 ,   C 2 ). Để diện tích (H) bằng  32/3 thì giá trị của k bằng

Nguyên hàm của hàm $$ y = 2 e tan   x 1 + c o s 2 x  là

Cho $$ I = ∫ 0 1 x 3 + 3 x 2 - x - 3 ( x 2 + 2 x + 3 ) 2 d x = a ( ln b - 1 ) . Khi đó $$ 4 a 2 + b 2  bằng

Cho $$ z = a + b i ,   a , b ∈ R $$ ,   z = 5 . Khi đó $$ 3 a + 4 b  lớn nhất khi

Cho S.ABCD, ABCD là hình chữ nhật có AB=2a; AD=2a. Các cạnh bên bằng nhau và bằng $$ a 2 .Góc tạo bởi giữa cạnh bên và đáy bằng $$ α . Khi đó $$ tan α

Cho hình trụ nội tiếp mặt cầu thảo mãn chiều cao của trụ băng bán kính mặt cầu. gọi Vt, Vc lần lượt là thể tích của hình trụ và hình cầu. Khi đó tỉ số thể tích  Vt/Vc bằng

Trong không gian Oxyz cho đường thẳng $$ ( d ) :   x - 1 2 = y - 2 - 1 = z - 3 1  và mặt phẳng   $$ ( P ) :   2 x + y + z = 0 . Phương trình đường thẳng qua giao điểm của đường thẳng (d) với  (P), nằm trên mặt phẳng (P) và vuông góc với đường thẳng d là.

Cho A(0;2;-2); B(-3;1;-1); C(1;m+2;0); D(1;m+2;0). Để A, B, C, D không là 4 đỉnh của tứ diện thì m thỏa mãn

Trong không gian Oxyz cho ba điểm A(1;1;1), B(-3;11;-1), C(4;m-1;0), D(1;m+2;0). Điểm  M(a;b;c) thuộc mặt phẳng $$ ( α ) :   2 x - y + 2 z + 7 = 0  sao cho biểu thức   $$ P = 3 M A ¯ + 5 M B ¯ - 7 M C ¯  đạt giá trị nhỏ nhất. Tính a+b+c

Cho tam giác ABC cân tại A. biết rằng độ dài cạnh BC, trung tuyến AM và độ dài cạnh AB theo thứ tự đó lập thành một cấp số nhân có công bội q. tính công bội q của cấp số nhân đó

Cho hàm số $$ y = 2 x x - 1 (C). Giá trị m để hàm số y=mx=m+2 giao với (C) tại 2 điểm phân biệt A, B sao cho AB ngắn nhất là

Một vật chuyển động với vận tốc v(t) và gia tốc $$ a ( t ) = 3 2 t + 1 ( m / s 2 ) . Vận tốc của vật  sau 10s từ thời điểm t=0 có giá trị xấp xỉ 8,6 cm/s. Vận tốc ban đầu bằng

Gọi $$ z 1 ,   z 2 ,   z 3 ,   z 4  là nghiệm của phương trình $$ ( z - 1 2 z - i ) 4 =1. Giá trị của  $$ ( z ₁ .   z ₂ .   z ₃ . z ₄ ) 2   bằng

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D, AD=AB=2a, CD=a góc giữa (SBC) với đáy bằng $$ 60 ° , I là trung điểm của AD, (SBI), (SCI) vuông góc với đáy. Thể tích S.ABCD bằng

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, $$ A B = a ,   A C = a 3 ,   B C = 2 a . Tam giác SBC cân tại S, tam giác SCD vuông tại C. Khoảng cách từ D đến mặt phẳng (SBC) bằng $$ a 3 3 . Chiều cao SH của hình chóp là

Cho A(1;2;3), B(4;0;1), C(4;8;1) và điểm M $$ ∈ ( S ) : x 2 + y 2 + z 2 = m ,   m > 0  thỏa mãn mặt cầu tâm M tiếp xúc với ba cạnh AB, BC, CA. Khi đó, m nhỏ nhất là

Cho f(x)+0 (*) có tổng các nghiệm dương nhỏ nhất bằng   $$ π 8 n 2 + π 4 n ,   n ∈ R ,   n ≥ 1   . Phương trình nào sau đây là phương trình hệ quả của (*)?

Tung một con xúc sắc n lần. Tim giá trị nhỏ nhất của n để xác suất xuất hiện mặt 6 chấm hai lần nhỏ hơn 0,001