Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 (tiếp theo) có đáp án

Cho hàm số \(y = \frac{{2x - 1}}{{x - 2}}\). Khẳng định nào sau đây đúng?

Cho lăng trụ tứ giác đều có cạnh bằng a và cạnh bên bằng 2a. Diện tích xung quanh của hình lăng trụ đã cho bằng

Thể tích của khối cầu tiếp xúc với tất cả các cạnh của hình lập phương cạnh \(2\sqrt 2 \) bằng

Đồ thị hàm số \(y = \frac{{2x + 1}}{{4 - {x^2}}}\) có bao nhiêu tiệm cận?

Cho \(P = \sqrt[3]{a}.{a^{\frac{1}{3}}},\,\,a > 0\). Khẳng định nào sau đây đúng?

Số giao điểm của đồ thị hàm số \(y = {x^3} - 4x + 1\) và đường thẳng \(y = x + 1\) bằng:

Bất phương trình \({\left( {\frac{e}{2}} \right)^{x - 1}} \le {\left( {\frac{e}{2}} \right)^{2x + 3}}\) có nghiệm là

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

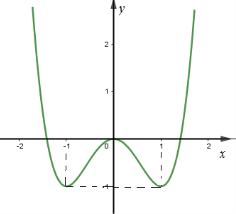
Tập nghiệm S của bất phương trình \({\log _{\frac{1}{2}}}\left( {3x - 2} \right) > {\log _{\frac{1}{2}}}\left( {4 - x} \right)\) là

Cho biểu thức \(A = {\log _{\sqrt a }}{a^2} + {\log _{\frac{1}{2}}}{4^a},\,\,a > 0,\,\,a e 1\). Khẳng định nào sau đây đúng?

Số giao điểm của đồ thị hàm số \(y = \left| {x - 1} \right|\left( {\frac{1}{3}{x^2} - 2\left| x \right| + 3} \right)\) với trục hoành là

Một hình đa diện có ít nhất bao nhiêu đỉnh?

Tính đạo hàm của hàm số \(y = {x^e} + {e^x}\)

Hàm số \(y = {x^3} - 3x\) có giá trị cực đại bằng

Cho hàm số \(y = \frac{{{x^2} - 3x + 3}}{{x - 1}}\). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn \(\left[ { - 1;\frac{1}{2}} \right]\). Tính tích M.m.

Diện tích toàn phần của hình trụ có thiết diện qua trục là hình vuông cạnh a bằng

Cho khối chóp S.ABC có ba cạnh SA, SB, SC cùng độ dài bằng a và vuông góc với nhau từng đôi một. Thể tích của khối chóp S.ABC bằng

Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có bảng biến thiên như hình vẽ

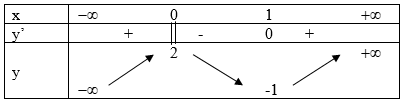
Khẳng định nào sau đây đúng?

Thể tích của khối bát diện đều cạnh a bằng

Trong không gian, cho hai điểm phân biệt A, B cố định. Xét điểm M di động luôn nhìn đoạn AB dưới một góc vuông. Hỏi điểm M thuộc mặt nào trong các mặt sau?

Cho phương trình \({\log _5}\left( {{x^2} + x + 1} \right) = 1\). Khẳng định nào sau đây đúng?

Phương trình \({\left( {{x^4}} \right)^{\frac{1}{{\sqrt 2 }}}} = {4^{\sqrt 2 }}\) có bao nhiêu nghiệm thực?

Hàm số \(y = \sqrt {{x^2} - x} \) nghịch biến trên khoảng

Cho hàm số \(y = {\log _2}x\). Xét các phát biểu

(1) Hàm số \(y = {\log _2}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) .

(2) Hàm số \(y = {\log _2}x\) có một điểm cực tiểu.

(3) Đồ thị hàm số \(y = {\log _2}x\) có tiệm cận.

Số phát biểu đúng là

Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số \(y = f\left( x \right)\) là:

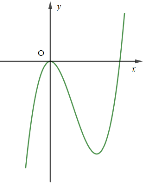
Các tiệm cận của đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) là

Cắt một khối nón bởi mặt phẳng đi qua trục của nó, ta được một tam giác vuông cân có diện tích bằng 8. Khẳng định nào sau đây sai ?

Tổng tất cả các nghiệm của phương trình \({4^x} - {3.2^{x + 1}} + 8 = 0\)

Hàm số nào sau đây có giá trị nhỏ nhất trên đoạn \(\left[ {0;2} \right]\) bằng –2 ?

Khối mười hai mặt đều là khối đa diện đều loại

Cho mặt nón có chiều cao \(h = 6\), bán kính đáy \(r = 3\). Hình lập phương ABCD.A’B’C’D’ đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong cùng một mặt phẳng đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài đường chéo của hình lập phương bằng

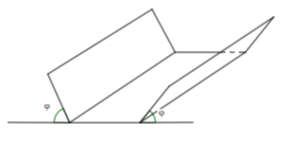
Bạn Nam làm một cái máng thoát nước mưa, mặt cắt là hình thang cân có độ dài hai cạnh bên và cạnh đáy đều bằng 20cm, thành máng nghiêng với mặt đất một góc \(\varphi \,\left( {{0^0} < \varphi < {{90}^0}} \right)\). Bạn Nam phải nghiêng thành máng một góc trong khoảng nào sau đây để lượng mưa thoát được là nhiều nhất?

Theo thống kê dân số năm 2017, mật độ dân số của Việt Nam là 308 người/\(k{m^2}\) và mức tăng trưởng dân số là năm. Với mức tăng trưởng như vậy, tới năm bao nhiêu mật độ dân số Việt Nam đạt 340 người 1,03%/\(k{m^2}\)

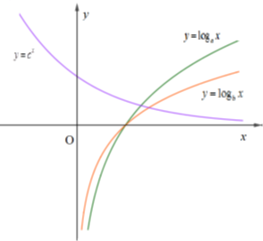
Cho các hàm số \(y = {\log _a}x,\,\,\,y = {\log _b}x\) và \(y = {c^x}\) (với a, b, c là các số dương khác 1) có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?

Biết rằng phương trình \({5^{2x + \sqrt {1 - 2x} }} - m{.5^{1 - \sqrt {1 - 2x} }} = {4.5^x}\) có nghiệm khi và chỉ khi \(m \in \left[ {a;b} \right]\), với m là tham số. Giá trị của \(b - a\) bằng

Cho phương trình \({\log _4}\left( {{x^2} - 4x + 4} \right) + {\log _{16}}{\left( {x + 4} \right)^2} - m = 0\). Tìm tất cả các giá trị của tham số thực m để phương trình đã cho có 4 nghiệm phân biệt.

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, \(AB = BC = 2,\,\,AD = 4\); mặt bên SAD nằm trong mặt phẳng vuông góc với đáy và có diện tích bằng 6. Thể tích khối S.BCD bằng

Cho tứ diện ABCD có \(AB = x\) thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.

Cho hình chóp tam giác đều S.ABC với \(SA = \sqrt 6 ,\,\,AB = 3\). Diện tích của mặt cầu có tâm A và tiếp xúc với mặt phẳng (SBC) bằng

Đồ thị của hàm số nào sau đây có ba tiệm cận?

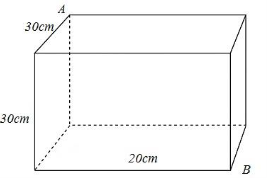
Một khối gỗ hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là 30cm, 20cm và 30cm (như hình vẽ). Một con kiến xuất phát từ điểm A muốn tới điểm B thì quãng đường ngắn nhất nó phải đi là bao nhiêu cm?

Cho hàm số \(y = \frac{{{x^4} + 3}}{x}\) có giá trị cực đại \({y_1}\) và giá trị cực tiểu \({y_2}\). Giá trị của \(S = {y_1} - {y_2}\) bằng

Cho hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) có đồ thị lần lượt như hình vẽ

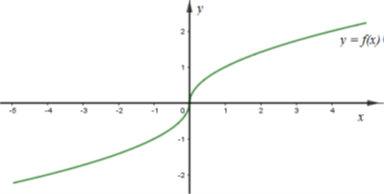
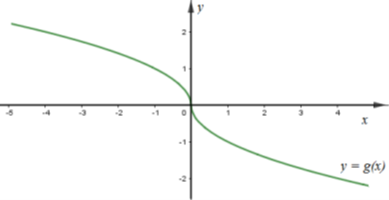
Đồ thị hàm số \(y = f\left( x \right).g\left( x \right)\) là đồ thị nào dưới đây?

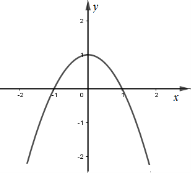
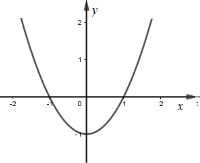
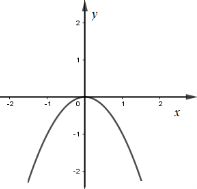
Phương trình \({e^x} - {e^{\sqrt {2x - 1} }} = 1 - {x^2} + 2\sqrt {2x + 1} \) có nghiệm trong khoảng nào sau đây?

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, \(SA \bot \left( {ABCD} \right)\) và \(SA = a\). Gọi E là trung điểm của cạnh AB. Diện tích mặt cầu ngoại tiếp hình chóp bằng .SBCE

Gọi giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y = \ln x\) trên đoạn \(\left[ {\frac{1}{{{e^2}}};e} \right]\) lần lượt là m và M. Tích M.m bằng

Phương trình \({3.9^x} - {7.6^x} + {2.4^x} = 0\) có hai nghiệm \({x_1},\,{x_2}\). Tổng \({x_1} + {x_2}\) bằng

Phương trình \({\left| x \right|^3} - 3{x^2} - {m^2} = 0\) (với m là tham số thực) có nhiều nhất bao nhiêu nghiệm phân biệt

Cho hàm số \(y = \frac{{2x + 3}}{{x - 2}}\) có đồ thị \(\left( C \right)\). Có bao nhiêu giá trị thực của tham số m để đường thẳng \(y = 2x + m\) cắt đồ thị \(\left( C \right)\) tại hai điểm phân biệt mà tiếp tuyến của t\(\left( C \right)\) ại hai điểm đó song song với nhau?