Đề thi THPT Quốc gia năm 2021 ( có đáp án)

Hàm số $y=\frac{x+1}{x-1}$có bao nhiêu điểm cực trị?

Cho các số phức z thỏa mãn $\left.z-i\right|=5$. Biết rằng tập hợp điểm biểu diễn số phức $\omega =iz+1-i$là đường tròn. Tính bán kính r của đường tròn đó.

Số hạng chứa $x^3{y}^3$trong khai triển ${\left(x+2y\right)}^6$thành đa thức là:

Tìm tập nghiệm S của bất phương trình ${\left(\frac{3}{4}\right)}^{2x-4}>{\left(\frac{3}{4}\right)}^{x+1}$

Cho hàm sốf (x) thỏa mãn $f^{\text{'}}\left(x\right)$ $=-\cos \left(x\right)$và $f\left(0\right)=2019$. Mệnh đề nào dưới đây đúng?

Cho khối nón có bán kính đáy $r=\sqrt{3}$và chiều cao h = 4. Tính thể tích V của khối nón đã cho.

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(\alpha \right):x-y+2z=1$. Trong các đường thẳng sau, đường thẳng nào vuông góc với $\left(\alpha \right)$

Cho hình bình hành ABCD. Tìm mệnh đề đúng?

Cho số phức $z=-4+i$. Biểu diễn hình học của z là điểm nào trong các điểm sau?

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có phương trình ${\left(x-1\right)}^2+{\left(y+3\right)}^2+z^2=4$. Tìm tọa độ tâm I và bán kính R của mặt cầu đó.

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số $y=\frac{1+3x}{2x-1}$

Cho các số phức z thỏa mãn $\left.z-i\right|=5$. Biết rằng tập hợp điểm biểu diễn số phức $\omega =iz+1-i$là đường tròn. Tính bán kính r của đường tròn đó.

Số cạnh của một hình chóp bất kì luôn là

Cho hai số dương a, b (a ≠ 1). Mệnh đề nào dưới đây sai:

Cho hình phẳng (D) giới hạn bởi đồ thị hàm số $y=\sqrt{x}$, hai đường thẳng x = 1, x = 2 và trục hoành. Tính thể tích V của khối tròn xoay tạo thành khi quay (D) quanh trục hoành.

Tập nghiệm của bất phương trình ${16}^x-5.4^x+4\ge 0$là $\left(-\infty ;\left.a\right]\cup b;+\infty \right)$. Tính 2a + b

Cho hàm số $y=f\left(x\right)$có đạo hàm trên $\left(a;b\right)$. Mệnh đề nào sau đây sai?

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $d:\begin{array}{l}x=1-t\\ y=-2+2t\\ z=1+t\end{array}$. Vectơ nào dưới đây là vectơ chỉ phương của d?

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A (3;2;1), B (-1;3;2), C (2;4;- 3). Tích vô hướng $\overrightarrow{AB}.\overrightarrow{AC}$bằng

Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y=\frac{2x+1}{x-m}$có tiệm cận đứng

Cho hai số thực x, y thỏa mãn phương trình x+2i= 3+4yi . Khi đó giá trị của x và y là:

Trong các mệnh đề sau đây, mệnh đề nào đúng?

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a cạnh bên bằng 3a. Tính thể tích V của khối chóp đã cho.

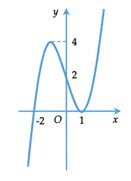
Đường cong hình bên dưới là đồ thị của hàm số nào?

Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng $\left(P\right):x+y+z+1=0$và hai điểm $A\left(1;-1;2\right)$; $B\left(2;1;1\right)$. Mặt phẳng $\left(Q\right)$chứa A, B và vuông góc với mặt phẳng (P). Mặt phẳng (Q) có phương trình là:

Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA=2a, AB = a, BC = $a\sqrt{3}$. Tính bán kính R của mặt cầu ngoại tiếp hình chóp

Trong các mệnh đề sau, mệnh đề nào SAI?

Biết rằng $\underset{2}{\overset{3}{\int }}x\ln xdx=m\ln 3+n\ln 2+p$, trong đó m, n, p $\in Q$. Tính m + n + 2p:

Đồ thị hàm số $y=x^4-4x^2$có bao nhiêu tiếp tuyến song song với trục hoành?

Cho các mệnh đề sau:

1. Nếu hàm số $y=f\left(x\right)$ liên tục, có đạo hàm tới cấp hai trên  $\left(a;b\right);x_0\in \left(a;b\right)$ và   $\begin{array}{l}f\text{'}\left(x_0\right)=0\\ f\text{'}\text{'}\left(x_0\right)\ne 0\end{array}$ thì x₀ là một điểm cực trị của hàm số.

2. Nếu hàm số $y=f\left(x\right)$xác định trên [a;b] thì luôn tồn tại giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

3. Nếu hàm số $y=f\left(x\right)$liên tục trên [a;b] thì hàm số có đạo hàm tại mọi x thuộc [a;b].

4. Nếu hàm số $y=f\left(x\right)$có đạo hàm trên [a;b] thì hàm số có nguyên hàm trên [a;b]

   Số mệnh đề đúng là:

Khi tính nguyên hàm $\int \frac{x-3}{\sqrt{x+1}}dx$, bằng cách đặt $u=\sqrt{x+1}$ta được nguyên hàm nào?

Gọi S là tổng tất cả các nghiệm của phương trình $2{\cos }^{2}2x+5\cos 2x-3=0$trong khoảng $\left(0;2018\pi \right)$. Tính S.

Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn $\left(C\right):{\left(x+1\right)}^2+{\left(y-2\right)}^2=9$và điểm $I\left(-3;3\right)$. Đường thẳng đi qua điểm I và cắt đường tròn (C) tại hai điểm A và B. Tiếp tuyến của A và B cắt nhau tại M. Biết điểm M thuộc đường thẳng x+3y-4=0. Tính $P=\frac{2a+3b}{c}$

Một người lập kế hoạch gửi tiết kiệm ngân hàng như sau: Đầu tháng 1 năm 2019, người đó gửi 10 triệu đồng; sau mỗi đầu tháng tiếp theo, người đó gửi số tiền nhiều hơn 10% so với số tiền đã gửi ở tháng liền trước đó. Biết rằng lãi suất ngân hàng không đổi là 0,5% mỗi tháng và được tính theo hình thức lãi kép. Với kế hoạch như vậy, đến hết tháng 12 năm 2020, số tiền của người đó trong tài khoản tiết kiệm là bao nhiêu? (kết quả làm tròn đến hàng nghìn)

Cho hàm số $y=f\left(x\right)=x^3-\left(2m-1\right)x^2+\left(2-m\right)x+2$. Tập tất cả các giá trị của m để đồ thị hàm số $y=f\left(\left.x\right|\right)$có 5 điểm cực trị là $\left(\frac{a}{b};c\right)$với a, b, c là các số nguyên và $\frac{a}{b}$là phân số tối giản. Tính a + b + c.

Một cửa hàng bán cam với giá bán mỗi kg là 50.000 đồng. Với giá bán này thì cửa hàng chỉ bán được khoảng 40kg. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi kg 5000 đồng thì số kg bán đươc tăng thêm là 50kg. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi kg là 30.000 đồng:

Gọi S là tổng tất cả các giá trị nguyên m < 64 để phương trình ${\log }_5\left(2-x\right)={\log }_5\left(x+m\right)$có nghiệm. Tìm S:

Gọi S là tổng tất cả các số thực m để phương trình $z^2-2z+1-m=0$có nghiệm thức z thỏa mãn $\left.z\right|=2$. Tính S

Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp S.ABC bằng $\frac{a^3}{6}$. Tính bán kính r mặt cầu nội tiếp của hình chóp S.ABC.

Cho hai số phức u, v thỏa mãn $\left.u\right|=\left.v\right|=10$và $\left.3u-4v\right|=\sqrt{2018}$. Tính $M=\left.4u+3v\right|$

Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;0;-1) và mặt phẳng $\left(P\right):x+y-z-3=0$. Gọi (S) là mặt cầu có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho diện tích tam giác OIA bằng $\frac{\sqrt{17}}{2}$. Tính bán kính R của mặt cầu (S).

Cho hàm số $y=\frac{2x-1}{x-1}$có đồ thị (C) . Gọi M,N là hai điểm phân biệt thuộc (C) có tọa độ là những số nguyên, trong đó $x_M>x_N$. Điểm P (a;b) thuộc (C) sao cho tam giác MNP cân tại M. Tính a + b:

Đáp án A.

F lần lượt là trung điểm của các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC). Tính thể tích V của khối chóp S.ABC.

Cho hàm số $y=f\left(x\right)$liên tục trên $\mathrm{ℝ}$. Hàm số $y=f\text{'}\left(x\right)$có đồ thị như hình vẽ:

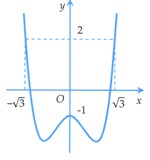
Điều kiện cần và đủ để bất phương trình $3f\left(x\right)\ge x^3-3x+m$, với m là tham số thực nghiệm đúng với $\forall x\in \left.-\sqrt{3};\sqrt{3}\right]$là

Trong không gian với hệ tọa độ Oxyz, cho các điểm A (1;0;0), B (3;2;0), C (-1;2;4). Gọi M là điểm thay đổi sao cho đường thẳng MA, MB, MC hợp với mặt phẳng (ABC) các góc bằng nhau; N là điểm thay đổi nằm trên mặt cầu $\left(S\right):{\left(x-3\right)}^2+{\left(y-2\right)}^2+{\left(z-3\right)}^2=\frac{1}{2}$. Giá trị nhỏ nhất của độ dài đoạn MN bằng:

Cho hai số thực x, y thỏa mãn điều kiện $3{\left(x+y\right)}^2+5{\left(x-y\right)}^2=4$. Hỏi có bao nhiêu giá trị nguyên của m thỏa mãn $m\left(2xy+1\right)=1009{\left(x^2+y^2\right)}^2+1009{\left(x^2-y^2\right)}^2$

Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có A (0;0;3), B (0;3;0), C(3;0;0), D(3;3;3). Hỏi có bao nhiêu điểm M (x;y;z) (với x, y, z nguyên) nằm trong tứ diện.

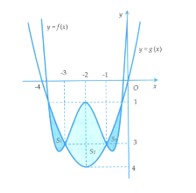
Cho hàm số $y=f\left(x\right)=x^4+16x^3+21x^2-20x+3$và hàm số $y=g\left(x\right)=a{\left(x+2\right)}^2+b$có đồ thị như hình vẽ. Biết rằng diện tích hình phẳng $S_1,S_2,S_3$giới hạn bởi đồ thị hàm số $y=f\left(x\right)$và đường cong $y=g\left(x\right)$lần lượt là m, n, p. Tính M = a – b + m – p + n.

Cho a, b, x, y, z là các số phức thỏa mãn: $a^2-4b=16+12i,x^2+ax+b+z=0,$ $y^2+ay+b+z=0$, $\left.x-y\right|=2\sqrt{3}$. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $\left.z\right|$. Tính M + m.

Cho hàm số $f\left(x\right)$thỏa mãn ${\left.xf\text{'}\left(x\right)\right]}^2+1=x^2\left.1-f\left(x\right).f\text{'}\text{'}\left(x\right)\right]$với mọi x dương. Biết $f\left(1\right)=f\text{'}\left(1\right)=1$tính $f^2\left(2\right)$

Cho bất phương trình ${\log }_2\sqrt{x^2-2x+m}+4\sqrt{{\log }_4\left(x^2-2x+m\right)}\le 5$. Biết $\left.a;b\right]$tập tất cả giá trị của tham số m để bất phương trình thỏa mãn với mọi x thuộc $\left.0;2\right]$. Tính a + b