Đề thi thử THPT QG môn Toán năm 2019 - Bộ đề 56

Cho hàm số $y = \frac{{ax + bx}}{{cx + d}}$ có đồ thị như hình vẽ. Khi đó

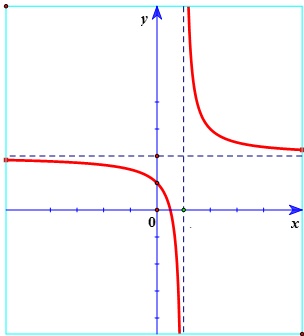
Giá trị của giới hạn $\mathop {\lim }\limits_{x \to {1^ + }} \frac{{{x^2} - 3x + 2}}{{{x^2} - x}}$ bằng:

Khoảng đồng biến của hàm số $y = - {x^3} + 3{x^2} - 1$ là:

Hàm số $y = - \frac{1}{4}{x^4} + \frac{1}{2}{x^2} - 3$ đạt cực tiểu tại:

Mô đun của số phức $z = \left( {2 - i} \right)\left( {1 - 3i} \right)\left( {1 + i} \right)$ là:

Cho hàm số $y = {x^4} + b{x^2} + c$ có đồ thị như hình vẽ. Khi đó

Cho hàm số y = f\left( x \right)\) xác định trên R và \(a, b, c là các hằng số. Khi đó

Cho số phức z thỏa mãn $z - \left( {2 + 3i} \right)\overline z = 1 - 9i$ . Phần ảo của z là:

Phương trình $m\sin x + \left( {m + 1} \right){\rm{cos}}x = m - 1$ có nghiệm khi và chỉ khi:

Đặt a = {\log _2}3,b = {\log _2}7\). Khi đó \({\log _2}2016 bằng:

Cho \overrightarrow u = \left( {1;2;3} \right),\overrightarrow v = \left( {a;b;c} \right)\) và \(\overrightarrow {\rm{w}} = \left( {2;1; - 1} \right)\). Ta có \(\overrightarrow u ,\overrightarrow v ,\overrightarrow {\rm{w}} đồng phẳng khi và chỉ khi:

Cho các số thực dương a, b, c\) khác 1. Khi đó \({\log _c}\left( {ab} \right) bằng:

Diện tích hình phẳng giới hạn bởi parabol $y = {x^2} - 1$ và đường thẳng y = 3 là:

Gọi (P) là mặt phẳng đi qua điểm A(4;5;6) và cắt Ox, Oy, Oz lần lượt tại I, J, K sao cho A là trực tâm tam giác I, J, K. Phương trình mặt phẳng (P) là:

Cho điểm A(2;1;0) và đường thẳng \Delta :\frac{{x - 1}}{2} = \frac{{y + 1}}{1} = \frac{z}{{ - 1}}\). Gọi d là đường thẳng đi qua A, cắt và vuông góc với \(\Delta. Ta có:

Cho lăng trụ tam giác đều ABC.A’B’C’ có $AB = 2a,AA' = a\sqrt 3$. Thể tích của khối lăng trụ bằng:

Nếu một khối trụ có thể tích bằng 125\pi\) và có diện tích xung quanh bằng \(25\pi thì có bán kính đáy bằng:

Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 lựa chọn, trong đó chỉ 1 lựa chọn là trả lời đúng. Giả sử mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai bị trừ 2 điểm. Một học sinh không học bài nên đánh ngẫu nhiên các câu trả lời. Xác suất để hịc sinh này được nhận được tối đa 1 điểm là:

Biết rằng đồ thì \left( {C'} \right):y = f\left( x \right)\) đối xứng với đồ thị \(\left( C \right):y = \frac{{x + 3}}{{x - 2}} qua Oy. Khi đó

Giả sử f\left( { - x} \right) = - f\left( x \right)\) với mọi \(x \in \left[ { - 1;1} \right]\) và \(\int\limits_0^1 {f\left( x \right)dx = 2} \) . Khi đó \(\int\limits_{ - 1}^1 {f\left( x \right)dx} bằng:

Trong không gian Oxyz điểm nào dưới đây là hình chiếu vuông góc của điểm A(3;5;2) trên mặt phẳng Oxy?

Cho số phức z thỏa mãn {z^2} + z + 1 = 0\). Khi đó \({z^{2019}} - \frac{1}{{{z^{2020}}}} bằng:

Gọi (H) là hình phẳng giới hạn bởi các đường thẳng $y = \sin x;y = 0;0 \le x \le \pi$. Quay (H) xung quanh trục Ox ta được khối tròn xoay có thể tích là:

Cho các điểm A(2;0;1), B(1;0;0), C(1;1;1) và cho mặt phẳng $\left( P \right):x + y + z - 2 = 0$. Phương trình mặt cầu đi qua A, B, C và có tâm thuộc (P) là:

Cho số phức z thỏa mãn \left| z \right| = 2\). Biết rằng tập hợp các điểm biểu diễn số phức \({\rm{w}} = \left( {2 + 4i} \right)z - 4 - 2i trên mặt phẳng phức là một đường tròn. Tâm của đường tròn có hoành độ bằng:

Cho a > 0, b > 0 thỏa mãn {a^2} + {b^2} = 7ab\). Khi đó \({\log _2}a + {\log _2}b bằng:

Hàm số y = \frac{{x + m}}{{x - m}}\) đồng biến trên khoảng \(\left( { - 1; + \infty } \right) khi và chỉ khi:

Cho a > 0, b > 0 thỏa mãn ${\log _9}a = {\log _{12}}b = {\log _{16}}\left( {a + 2b} \right)$. Khi đó

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = x - \sqrt {4 - {x^2}}$. Khi đó M + m bằng:

Cho tích phân I = \int_0^3 {\frac{x}{{1 + \sqrt {1 + x} }}dx} \). Bằng cách biến đổi \(t = \sqrt {1 + x} \) ta được \(I = \int_1^2 {f\left( t \right)dt} , với:

Gọi x_1, x_2\) là hai nghiệm của phương trình \({2^{{x^2} + x + \frac{5}{2}}} = 4\sqrt 2 \). Khi đó \(x_1x_2 bằng:

Một người gửi tiết kiệm 58 triệu đồng theo kỳ hạn 1 tháng. Sau 8 tháng người đó rút cả vốn lẫn lãi một lần và nhận được 61.329.000 đồng. hỏi lãi suất tiền gửi là bao nhiêu ?

Cho ba điểm M, N, P nằm trên một mặt cầu sao cho MN = 3, MP = 4, NP = 5 và khoảng cách từ tâm mặt cầu tới mặt phẳng (MNP) bằng 2. Thể tích khối cầu tương ứng bằng:

Người ta có thể tích số các chữ số của số tự nhiên N theo công thức \left[ {\log N} \right] + 1\), trong đó \(\left[ {\log N} \right] \) là phần nguyên của \(\log N\) tức là số tự nhiên lớn nhất mà vẫn bé lớn \(\log N\). Hãy tính số các chữ số của số \({2^{2017}}{.3^{2017}}

Một vật bắt đầu chuyển động trên trục số Ox với gia tốc được tính theo công thức a\left( t \right) = {t^2} + 2t\,\,\left( {m/{s^2}} \right)\) và vận tốc ban đầu \({v_0}\left( t \right) = 3\,\,\left( {m/s} \right). Quãng đường vật đi được trong khoảng thời gian 5 giây đầu là:

Phương trình {\rm{co}}{{\rm{s}}^6}x - 9{\cos ^4}x + 15{\cos ^2}x - 9 + m = 0\) có 4 nghiệm phân biệt thuộc đoạn \(\left[ {0;2\pi } \right] khi và chỉ khi:

Cho \int\limits_0^{\frac{{\sqrt 3 }}{2}} {f\left( x \right)dx = 2} \). Khi đó giá trị của tích phân \(I = \int\limits_0^{\frac{\pi }{3}} {f\left( {\sin \left( {2x + \frac{\pi }{3}} \right)} \right)c} os\left( {2x + \frac{\pi }{3}} \right)dx là:

Biết rằng hai mặt cầu \left( S \right):{x^2} + {y^2} + {z^2} - 2x + 4y + 6z - 1 = 0\) và \(\left( {S'} \right):{\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} + {z^2} = 9 cắt nhau theo một đường tròn. Phương trình mặt phẳng chứa đường tròn đó là:

Biết rằng {\log _2}\sqrt {{2^{\sqrt 3 }}.\sqrt[3]{4}} + {\log _9}\left( {{3^{\sqrt 3 }}.\sqrt[3]{3}} \right) = a\sqrt 3 + b\) với \(a, b là các số hữu tỉ. Khi đó:

Một chậu nước A hình lập phương có kích thước 4cm x 4cm x 4cm chứa đầy nước. Người ta rót nước từ chậu A vào chậu nước B hình lăng trụ đứng có đáy là tam giác đều cạnh 3cm và đường cao 16cm đến khi hộp B đầy nước. Độ cao của mực nước còn lại trong A gần bằng:

Cho số phức z thỏa mãn \left| z \right| = 2\). Biết rằng tập hợp các điểm biểu diễn số phức \({\rm{w}} = z + \frac{1}{z} trong mặt phẳng phức là một e-lip. Ta có tiêu cự của e-lip bằng:

Cho hai đường thẳng d và d’ song song nhau. Trên d lấy 17 điểm phân biệt và trên d’ lấy 20 điểm phân biệt. Số tam giác có các đỉnh được chọn từ 37 điểm này là:

Ông An vay ngân hàng 10 triệu đồng theo thể thức lãi kép với lãi suất 5,6%/năm. Ngay sau đó, ông An cho ông Bình vay lại 10 triệu này theo thể thức lãi kép với lãi suất 1,2%/tháng. Sau bốn năm, ông Bình trả toàn bộ số tiền cả vốn lẫn lãi cho ông An và ông An cũng trả toàn bộ số tiền cả vốn lẫn lãi cho ngân hàng. Số tiền còn lại ông An nhận được là bao nhiêu (làm tròn đến chữ số hàng trăm) ?

Hệ số không chứa x trong khai triển nhị thức Newton ${\left( {\sqrt[4]{{{x^3}}} + \frac{1}{{\sqrt[3]{{{x^2}}}}}} \right)^{17}}$ là:

Hàm số $y = 2{x^3} - 3\left( {m + 1} \right){x^2} + 6mx + 1$ nghịch biến trên khoảng (1;3) khi và chỉ khi:

Gọi (P) là mặt phẳng đi qua điểm I(1;3;3) và cắt các tia Ox, Oy, Oz lần lượt tại A, B, C. Thể tích tứ diện OABC đạt giá trị nhỏ nhất khi và chỉ khi:

Cho hàm số y = f\left( x \right)\) xác định trên R và thỏa mãn \(f\left( 0 \right) = f'\left( 0 \right) = 1\) và \(\left( {f'{{\left( x \right)}^2}} \right) + f\left( x \right)f''\left( x \right) = 15{x^4} + 12x\) với mọi \(x \in R\). Giá trị của \({\left( {f\left( 1 \right)} \right)^2}bằng:

Người ta thả một quả cầu bằng đồng vào một bồn nước hình trụ với đường kính là 180 cm. Sau khi thả, quả cầu chìm hẳn trong nước và mực nước trong bồn dâng cao thêm 18cm(nước không tràn ra khỏi bồn). Bán kính của quả cầu đồng là:

Cho hàm số f(x)\) dương và liên tục trên đoạn [0;1] thỏa mãn \({e^x}.{\left[ {f\left( x \right)} \right]^2} - f'\left( x \right) = 0,\forall x \in \left[ {0;1} \right]\) và \(f\left( 0 \right) = \frac{1}{e}\). Khi đó \(f(1) bằng:

Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \frac{{{x^3} + 2{x^2} + x}}{{{x^4} + 2{x^2} + 1}}$. Khi đó M – m bằng: