Trắc nghiệm Toán 10 (có đáp án): Bài tập ôn tập chương II

Tìm tập xác định của hàm số $$ y = x − 2 x 3 + x 2 − 5 x − 2  

Tìm tập xác định của hàm số  $$ y = x + 2 x x 2 − 4 x + 4   

Tìm tập xác định của hàm số  $$ y = 1 x    khi    x ≥ 1 x + 1 ​​   khi    x < 1   

Cho hàm số:  $$ y = m x x − m + 2 − 1 với m là tham số. Tìm m để hàm số xác định trên (0; 1)

Xét tính chẵn, lẻ của hàm số  $$ f ( x ) = 3 x 3 + 2 x 3  

Xét tính chẵn lẻ của hàm số  $$ f ( x ) = − 1    k h i    x < 0 0    k h i    x = 0 1    k h i    x > 0  

Tìm m để hàm số:  $$ f ( x ) = x 2 ( x 2 − 2 ) + ( 2 m 2 − 2 ) x x 2 + 1 − m  là hàm số chẵn

Tìm m  để đồ thị hàm số sau nhận gốc tọa độ O làm tâm đối xứng y = $$ x 3 − ( $$ m 2 − 9) $$ x 2 + (m + 3)x + m − 3.

Tìm m  để đồ thị hàm số sau nhận trục tung làm trục đối xứng y = $$ x 4   −   ( m 2   −   3 m   +   2 ) x 3   +   m 2   −   1 .

Xét sự biến thiên của hàm số $$ y = 3 x − 1  trên khoảng (1; + $$ ∞ )

Xét sự biến thiên của hàm số  $$ y = 4 x + 5 + x − 1 trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình  $$ 4 x + 5 + x − 1 = 3  

Xét sự biến thiên của hàm số  $$ y = 4 x + 5 + x − 1 trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình  $$ 4 x + 5 + x − 1 = 4 x 2 + 9 + x  

Cho hàm số y = $$ mx 3   −   2 ( m 2   +   1 ) x 2   +   2 m 2   −   m . Tìm m để điểm M (−1; 2) thuộc đồ thị hàm số đã cho

Cho hàm số y = $$ mx 3   −   2 ( m 2   +   1 ) x 2   +   2 m 2     −   m . Tìm các điểm cố định mà đồ thị hàm số đã cho luôn đi qua với mọi m.

Tìm trên đồ thị hàm số y = $$ − x 3   +   x 2 + 3x − 4 hai điểm đối xứng nhau qua gốc tọa độ.

Tịnh tiến đồ thị hàm số y = $$ x 2 +1 liên tiếp sang phải 2 đơn vị và lên trên 1 đơn vị ta được đồ thị của hàm số nào?

Nêu cách tịnh tiến đồ thị hàm số y = −2 $$ x 2 để được đồ thị hàm số y = −2 $$ x 2 − 6x + 3.

Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết dd đi qua A (1; 3),B (2; −1)

Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua C (3; −2) và song song với $$ △ : 3x − 2y + 1 = 0

Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua M (1; 2) và cắt hai tia Ox, Oy tại P, Q sao cho  $$ S ΔOPQ  nhỏ nhất.

Cho hai đường thẳng d: y = x + 2m, d′: y = 3x + 2 (m là tham số). Tìm m để ba đường thẳng d, d′ và d′′: y = −mx + 2 phân biệt đồng quy.

Cho đường thẳng d: y = (m − 1)x + mvà d′: y = ( $$ m 2 − 1)x + 6. Tìm m để hai đường thẳng d, d′ song song với nhau

Cho đường thẳng d: y = (m − 1)x + m và d′: y = $$ m 2 − 1)x + 6.  Tìm m để đường thẳng d cắt trục tung tại A, d′ cắt trục hoành tại B sao cho tam giác OAB cân tại O

Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x $$ ∈ [−3; 4]

Cho hàm số f(x) = |2x − m|. Tìm m để giá trị lớn nhất của f(x)  trên [1; 2] đạt giá trị nhỏ nhất.

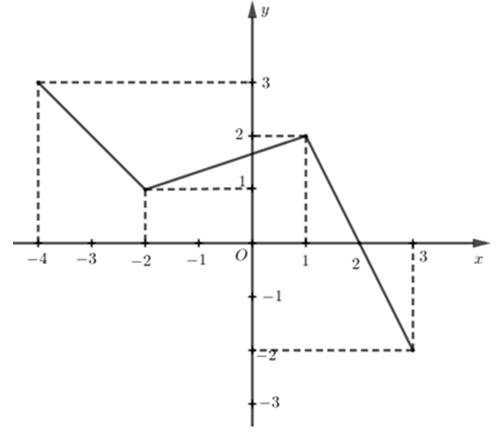
Cho đồ thị hàm số có đồ thị (C) (hình vẽ). Tìm tổng giá trị lớn nhất và nhỏ nhất của hàm số trên [−4;2]

Xác định parabol (P): y = a $$ x 2 + bx + c, a $$ ≠ 0 biết (P) đi qua A (2; 3) có đỉnh I (1; 2)

Xác định parabol (P): y = a $$ x 2 + bx + c, a $$ ≠ 0 biết c = 2 và (P) đi qua B (3; −4) và có trục đối xứng là  $$ x = − 3 2  

Xác định parabol (P): y = a $$ x 2 + bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng  $$ 3 4  khi x= $$ 1 2   và nhận giá trị bằng 1 khi x = 1.

Xác định parabol (P): y = a $$ x 2 + bx + c, a  $$ ≠ 0 đỉnh I biết (P) đi qua M (4; 3) cắt Ox tại N (3; 0) và P  sao cho $$ △ INP có diện tích bằng 1, biết hoành độ điểm P nhỏ hơn 3.

Tìm Parabol y = a $$ x 2 + 3x – 2, biết rằng parabol đó cắt trục Ox tại điểm có hoành độ bằng 2

Cho hàm số y = $$ x 2 − 6x + 8. Sử dụng đồ thị để tìm số điểm chung của đường thẳng y = m (−1 < m <0) và đồ thị hàm số trên.

Cho hàm số y = − $$ x 2 − 2x + 3. Hãy tìm giá trị nhỏ nhất của hàm số đã cho trên [−3; 1].

Cho phương trình $$ x 2 + 2 (m + 3)x + $$ m 2 – 3 = 0, m là tham số.

Tìm giá trị nhỏ nhất của hàm số  $$ y = x 4 + 2 x 2 + 1 3 − 3 x 2 + 1 3 + 1