Trắc nghiệm Toán 10 (có đáp án): Tổng hợp câu hay và khó chương II- Phần II

Tìm m để hàm số y = ${\mathrm{x}}^2$ − 2x + 2m + 3 có giá trị nhỏ nhất trên đoạn [2; 5] bằng −3.

Xác định các hệ số a và b để Parabol (P): y = a ${\mathrm{x}}^2$ + 4x – b có đỉnh I (-1; -5)

Cho parabol (P): y = a ${\mathrm{x}}^2$ + bx + c (a $\ne$ 0) có đồ thị như hình bên. Tìm các giá trị m để phương trình |ax2 + bx + c| = m có bốn nghiệm phân biệt.

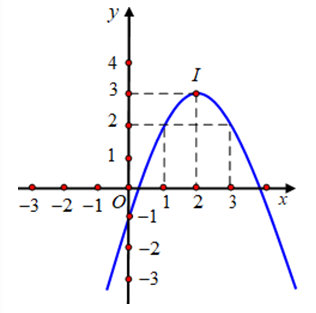
Tìm tất cả các giá trị mm để đường thẳng y = mx + 3 − 2m cắt parabol y = ${\mathrm{x}}^2$ − 3x − 5 tại 2 điểm phân biệt có hoành độ trái dấu.

Đường thẳng d: y = (m − 3)x − 2m + 1 cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB cân. Khi đó, số giá trị của m thỏa mãn là:

Các đường thẳng y = −5(x + 1); y = 3x + a; y = ax + 3 đồng quy với giá trị của a là

Tìm m để hàm số  $y=\frac{\sqrt{x-2m+3}}{x-m}+\frac{3x-1}{\sqrt{-x+m+5}}$  xác định trên khoảng (0; 1)

Tìm các giá trị thực của tham số m để hàm số  $y=\frac{x+m+2}{x-m}$ xác định trên (-1;2)

Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào một chiếc là 27 (triệu đồng) và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.

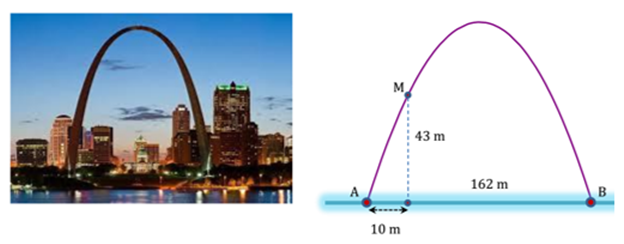
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).

Đồ thị hàm số y = x − 2m + 1 tạo với hệ trục tọa độ Oxy tam giác có diện tích bằng $\frac{25}{2}$. Khi đó m bằng:

Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; h là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.

Hỏi có bao nhiêu giá trị mm nguyên trong nửa khoảng (0; 2017] để phương trình | ${\mathrm{x}}^2$ − 4|x |−5| − m = 0 có hai nghiệm phân biệt?

Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2) và B (3; 4). Điểm P ( $\frac{\mathrm{a}}{\mathrm{b}}$; 0) (với  $\frac{\mathrm{a}}{\mathrm{b}}$ là phân số tối giản, b > 0) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính S = a + b.

Cho hàm số y = ${\mathrm{x}}^2$ − 2(m +  $\frac{1}{\mathrm{m}}$ )x + m (m > 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là ${\mathrm{y}}_1, {\mathrm{y}}_2$ thỏa mãn ${\mathrm{y}}_1-{\mathrm{y}}_2$ = 8. Khi đó giá trị của m bằng