Trắc nghiệm Ôn tập Toán 10 Chương 2 có đáp án (Tổng hợp)

Cho hàm số y = ax² + bx + c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?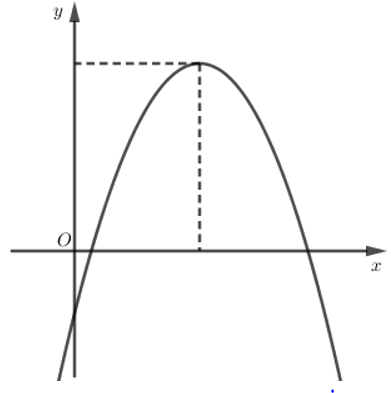

Cho hàm số: $$ y = m x x - m + 2 - 1 với m là tham số. Tìm m để hàm số xác định trên (0; 1)

Tìm m để hàm số: $$ f ( x ) = x 2 ( x 2 - 2 ) + ( 2 m 2 - 2 ) x x 2 + 1 - m là hàm số chẵn

Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua M (1; 2) và cắt hai tia Ox, Oy tại P, Q sao cho $$ S Δ O P Q nhỏ nhất.

Xét sự biến thiên của hàm số $$ y = 4 x + 5 + x - 1 trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình $$ 4 x + 5 + x - 1 = 3

Cho hai đường thẳng d: y = x + 2m, d′: y = 3x + 2 (m là tham số). Tìm m để ba đường thẳng d, d′ và d′′: y = −mx + 2 phân biệt đồng quy.

Cho đường thẳng d: y = (m − 1)x + m và d′: y = (m² − 1)x + 6. Tìm m để hai đường thẳng d, d′ song song với nhau

Cho đường thẳng d: y = (m − 1)x + m và d′: y = (m² − 1)x + 6. Tìm m để đường thẳng d cắt trục tung tại A, d′ cắt trục hoành tại B sao cho tam giác OAB cân tại O

Cho hàm số y = 3|x − 2| − |2x − 6| có đồ thị (C). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với x ∈ [−3; 4]

Cho hàm số f(x) = |2x − m|. Tìm m để giá trị lớn nhất của f(x) trên

[1; 2] đạt giá trị nhỏ nhất.

Xác định parabol (P): y = ax² + bx + c, a ≠ 0 biết hàm số có giá trị nhỏ nhất bằng $$ 3 4 khi x = $$ 1 2 và nhận giá trị bằng 1 khi x = 1.

Xác định parabol (P): y = ax² + bx + c, a ≠ 0 đỉnh I biết (P) đi qua

M (4; 3) cắt Ox tại N (3; 0) và P sao cho ΔINP có diện tích bằng 1, biết hoành độ điểm P nhỏ hơn 3.

Cho hàm số y = x² − 6x + 8. Sử dụng đồ thị để tìm số điểm chung của đường thẳng y = m (−1 < m <0) và đồ thị hàm số trên

Cho phương trình x² + 2 (m + 3)x + m² – 3 = 0, m là tham số.

Tìm m để phương trình có hai nghiệm x₁, x₂và P = 5(x₁ + x₂) − 2x₁x₂đạt giá trị lớn nhất.

Tìm giá trị nhỏ nhất của hàm số $$ y = x 4 + 2 x 2 + 1 3 - 3 x 2 + 1 3 + 1

Hàm số nào sau đây có đồ thị như hình dưới?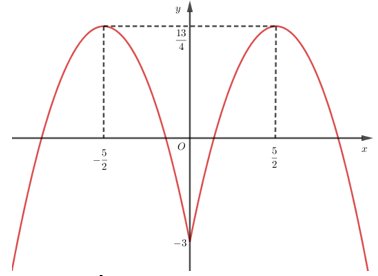

Đồ thị hàm số y = x² − 6|x| + 5.

Cho hàm số y = f(x) có bảng biến thiên như sau: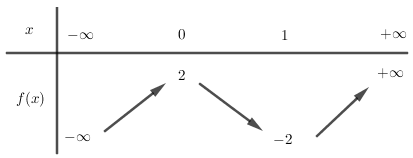

Với giá trị nào của tham số m thì phương trình |f(x) − 1| = m có bốn nghiệm phân biệt.

Cho hàm số f(x) = ax² + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình |f(x)| − 1 = m có đúng 2 nghiệm phân biệt.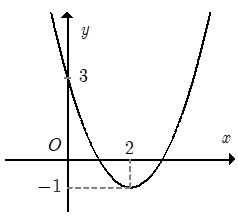

Một của hàng buôn giày nhập một đôi với giá là 40 USD. Cửa hàng ước tính rằng nếu đôi giày được bán với giá x USD thì mỗi tháng khách hàng sẽ mua (120 − x) đôi. Hỏi của hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?

Trong các hàm số sau có bao nhiêu hàm số có đồ thị nhận gốc tọa độ làm tâm đối xứng:

$$ y = x 2 + 1 ; y = x 5 + x 3 ; y = x ; y = x x 2 + 1 ; y = x 3 + x 2 ; y = x 2 - 2 x + 3 ; y = 3 - x + x + 3 x 2

Tìm m để hàm số y = x² − 2x + 2m + 3 có giá trị nhỏ nhất trên đoạn [2; 5] bằng −3.

Cho parabol (P): y = ax² + bx + c (a ≠ 0) có đồ thị như hình bên. Tìm các giá trị m để phương trình |ax² + bx + c| = m có bốn nghiệm phân biệt.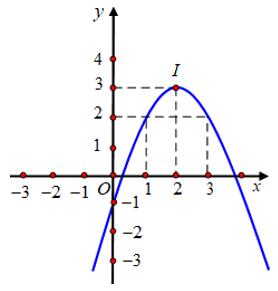

Đường thẳng d: y = (m − 3)x − 2m + 1 cắt hai trục tọa độ tại hai điểm A và B sao cho tam giác OAB cân. Khi đó, số giá trị của m thỏa mãn là:

Các đường thẳng y = −5(x + 1); y = 3x + a; y = ax + 3 đồng quy với giá trị của a là

Tìm m để hàm số $$ y = x - 2 m + 3 x - m + 3 x - 1 - x + m + 5 xác định trên khoảng (0; 1)

Tìm các giá trị thực của tham số m để hàm số $$ y = x + m + 2 x - m xác định trên

(-1;2)

Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).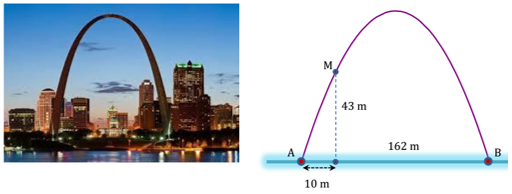

Đồ thị hàm số y = x − 2m + 1 tạo với hệ trục tọa độ Oxy tam giác có diện tích bằng $$ 25 2 . Khi đó m bằng:

Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây), kể từ khi quả bóng được đá lên; h là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.

Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng (0; 2017] để phương trình |x² − 4|x| − 5| − m = 0 có hai nghiệm phân biệt?

Trong mặt phẳng tọa độ Oxy, cho hai điểm A (1; 2) và B (3; 4). Điểm

P ( $$ a b ; 0) (với $$ a b là phân số tối giản, b > 0) trên trục hoành thỏa mãn tổng khoảng cách từ P tới hai điểm A và B là nhỏ nhất. Tính S = a + b

Cho hàm số y = x² − 2(m + $$ 1 m )x + m (m > 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là y₁, y₂thỏa mãn y₁ – y₂ = 8. Khi đó giá trị của m bằng

Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết d đi qua M (1; 2) và cắt hai tia Ox, Oy tại P, Q sao cho $$ S Δ O P Q nhỏ nhất.