Trang chủ Hỏi & đáp THPT Quốc gia Vật lý Câu hỏi số #2710

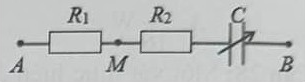
Đặt điện áp u= U 0 cosωt U 0 , ω không đổi) vào hai đầu đoạn mạch AB như hình bên. Biết R 1 =3 R 2 . Gọi Δφ là độ lệch pha giữa u A B và điện áp uMB. Điều chỉnh điện dung của tụ điện đến giá trị C 0 thì Δφ đạt cực đại. Khi điện dung có giá trị C=2 C 0 thì hệ số công suất của đoạn mạch AB lúc này bằng

Hình ảnh

A.  

0,97.

B.  

0,25.

C.  

0,89.

D.  

0,50.

Đáp án đúng là: B

Chuẩn hóa R 2 =1⇒ R 1 =3
Δφ=(φ)AB−(φ)MB=arctan−ZCR1+R2−arctan−ZCR2=arctan−ZC4−arctan−ZC1→\Delta \varphi = \left(\varphi\right)_{A B} - \left(\varphi\right)_{M B} = arctan \dfrac{- Z_{C}}{R_{1} + R_{2}} - arctan \dfrac{- Z_{C}}{R_{2}} = arctan \dfrac{- Z_{C}}{4} - arctan \dfrac{- Z_{C}}{1} \rightarrowshift solve đạo hàm


⇒ZC0=2\Rightarrow Z_{C 0} = 2
C=2C0⇒ZC=0,5ZC0=0,5.2=1C = 2 C_{0} \Rightarrow Z_{C} = 0 , 5 Z_{C 0} = 0 , 5 . 2 = 1
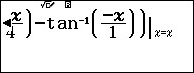
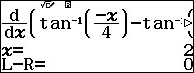
cosφ=R1+R2(R1+R2)2+ZC2=3+1(3+1)2+12≈0,97cos \varphi = \dfrac{R_{1} + R_{2}}{\sqrt{\left( R_{1} + R_{2} \right)^{2} + Z_{C}^{2}}} = \dfrac{3 + 1}{\sqrt{\left( 3 + 1 \right)^{2} + 1^{2}}} \approx 0 , 97. Chọn A
MNCâu 38: Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ M khối lượng m được treo thẳng đứng ở nơi có gia tốc trọng trường g=10 m/ s 2 . Khi vật ở vị trí cân bằng thì lò xo giãn 4cm. Treo thêm vật N phía dưới vật M bằng một sợi dây mảnh, nhẹ, không giãn. Sợi dây xuyên qua N bởi một lỗ nhỏ như hình vẽ. Ban đầu N được giữ đứng yên bởi một cái chốt, hệ cân bằng, khi đó lò xo giãn 10cm. Rút nhẹ chốt, N trượt trên dây thẳng đứng xuống. Biết lực ma sát giữa N và dây có độ lớn bằng 1 4 trọng lượng của N. Lấy π 2 =10 . Bỏ qua lực cản không khí. Khi N rời dây, nó có tốc độ là 2,25m/s. Biên độ dao động của M sau khi N rời khỏi dây gần giá trị nào sau đây nhất?
A. 4,5cm. B. 4,7cm. C. 1,6cm. D. 5,8cm.
Lời giải
Khi treo mỗi vật M thì lò xo giãn Δl0=mMgk=4cm\Delta l_{0} = \dfrac{m_{M} g}{k} = 4 c m


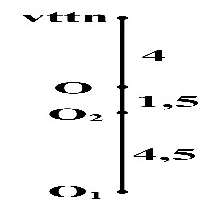
Khi N chưa trượt, hệ cân bằng, VTCB của M là O1, lò xo giãn 10 cm
OO1=mNgk=10−4=6cmO O_{1} = \dfrac{m_{N} g}{k} = 10 - 4 = 6 c m
Khi rút nhẹ chốt, N trượt xuống: T=Fms=0,25mNgT = F_{m s} = 0 , 25 m_{N} g
Vật M chịu thêm tác dụng của ngoại lực căng dây T nên VTCB của nó lúc này là O2
OO2=Tk=0,25mNgk=0,25.6=1,5cmO O_{2} = \dfrac{T}{k} = \dfrac{0 , 25 m_{N} g}{k} = 0 , 25 . 6 = 1 , 5 c m
Vật M dao động với biên độ: A1=O1O2=6−1,5=4,5cmA_{1} = O_{1} O_{2} = 6 - 1 , 5 = 4 , 5 c m và ω=gΔl0=100,04≈5π\omega = \sqrt{\dfrac{g}{\Delta l_{0}}} = \sqrt{\dfrac{10}{0 , 04}} \approx 5 \pi (rad/s)
Vật N chuyển động nhanh dần đều xuống dưới với giá tốc có độ lớn a=mNg−FmsmN=g−0,25g=7,5m/s2a = \dfrac{m_{N} g - F_{m s}}{m_{N}} = g - 0 , 25 g = 7 , 5 m / s^{2}
Khi N rời dây thì thời gian M và N đã chuyển động là: t=vNg=2,257,5=0,3st = \dfrac{v_{N}}{g} = \dfrac{2 , 25}{7 , 5} = 0 , 3 s
Chọn gốc tọa độ tại O, chiều dương hướng xuống
xM=OO2+Acos(ωt)=1,5+4,5cos(5π.0,3)=1,5cmx_{M} = O O_{2} + A cos \left( \omega t \right) = 1 , 5 + 4 , 5cos \left( 5 \pi . 0 , 3 \right) = 1 , 5 c m
vM=−ωAsin(ωt)=−5π.4,5.sin(5π.0,3)=22,5πcm/sv_{M} = - \omega A sin \left( \omega t \right) = - 5 \pi . 4 , 5 . sin \left( 5 \pi . 0 , 3 \right) = 22 , 5 \pi c m / s
Sau khi N rời dây, M có VTCB O nên M dao động với biên độ
A2=xM2+(vMω)2=1,52+(22,5π5π)2≈4,74cmA_{2} = \sqrt{x_{M}^{2} + \left( \dfrac{v_{M}}{\omega} \right)^{2}} = \sqrt{1 , 5^{2} + \left( \dfrac{22 , 5 \pi}{5 \pi} \right)^{2}} \approx 4 , 74 c m. Chọn B


 

Câu hỏi tương tự:

#5284 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt ( U 0 không đổi, ω thay đổi được) vào hai đầu đoạn mạch AB (như hình vẽ). Biết R=r và L=C R 2 . Khi ω= ω 1 và ω= ω 2 thì biểu thức điện áp giữa hai đầu cuộn dây (đoạn mạch MB ) lần lượt là u d 1 = U 1 2 cos ω 1 t + α 1 và u d 2 = U 2 2 cos ω 2 t + α 2 . Biết α 1 + α 2 = π 2 và 5 U 1 =3 U 2 . Tính hệ số công suất của đoạn mạch khi ω= ω 1 ?

Lượt xem: 89,910 Cập nhật lúc: 11:36 17/01/2025

#3654 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt ( U 0 và ω không đổi) vào hai đầu đoạn mạch gồm cuộn dây không thuần cảm mắc nối tiếp với tụ điện có điện dung C C thay đổi được). Khi C= C 0 thì cường độ dòng điện trong mạch sớm pha hơn u là φ 1 0 < φ 1 < π / 2 và điện áp hiệu dụng hai đầu cuộn dây là 60 V . Khi C=3 C 0 thì cường độ dòng điện trong mạch trễ pha hơn u là φ 2 =2π/3- φ 1 và điện áp hiệu dụng hai đầu cuộn dây là 180 V . Giá trị của U 0 gần giá trị nào nhất sau đây?

Lượt xem: 62,195 Cập nhật lúc: 05:46 17/01/2025

#2923 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt U 0 không đổi, ω thay đổi được ) vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Hiện tượng cộng hưởng điện xảy ra khi

Lượt xem: 49,731 Cập nhật lúc: 05:46 17/01/2025

#3489 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt U 0 > 0 vào hai đầu mạch điện R,L,C mắc nối tiếp (cuộn cảm thuần) thì trong mạch có dòng điện i= I 0 cos(ωt+φ) I 0 > 0 . Công suất tiêu thụ của mạch là

Lượt xem: 59,401 Cập nhật lúc: 05:46 17/01/2025

#2426 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt(V) U 0 , ω không đổi) vào hai đầu đoạn mạch AB mắc nối tiếp gồm đoạn mạch AM chứa điện trở R , đoạn mạch MN chứa tụ điện có điện dung C và đoạn NB chứa cuộn cảm có độ tự cảm L và điện trở r . Sử dụng một ampe kế lý tưởng theo các cách sau đây: mắc nối tiếp ampe kế với mạch điện thì số chỉ ampe kế là 1,8 A ; mắc song song ampe kế vào hai điểm A,M thì số chỉ ampe kế là 2,6 A; mắc song song ampe kế vào hai điểm M,N thì số chỉ ampe kế là 0,9 A. Nếu mắc song song ampe kế vào hai điểm A,N thì số chỉ ampe kế là

Lượt xem: 41,338 Cập nhật lúc: 04:22 17/01/2025

#3166 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt (với U 0 không đổi, ω thay đổi) vào hai đầu đoạn mạch nối tiếp gồm điện trở R , cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C . Khi ω= ω 0 trong mạch có cộng hưởng điện. Tần số góc ω 0 là

Lượt xem: 53,860 Cập nhật lúc: 14:42 17/01/2025

#43 THPT Quốc giaVật lý

Đặt điện áp xoay chiều u= U 0 cosωt U 0 > 0 ; ω > 0 vào hai đầu đoạn mạch R,L,C mắc nối tiếp. Hiện tượng cộng hưởng xảy ra khi

Lượt xem: 829 Cập nhật lúc: 05:47 17/01/2025

#3216 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp. Gọi Z L là cảm kháng, Z c là dung kháng. Độ lệch pha giữa điện áp u với cường độ dòng điện i trong mạch được xác định bằng công thức

Lượt xem: 54,763 Cập nhật lúc: 05:45 17/01/2025

#1577 THPT Quốc giaVật lý

Đặt điện áp u= U 0 cosωt vào hai đầu cuộn cảm thuần có độ tự cảm L . Tại thời điểm điện áp giữa hai đầu cuộn cảm có độ lớn cực đại thì cường độ dòng điện qua cuộn cảm bằng

Lượt xem: 26,897 Cập nhật lúc: 09:42 17/01/2025


Đề thi chứa câu hỏi này:

72. Đề thi thử TN THPT VẬT LÝ 2024 - Nguyễn Khuyến - Lê Thánh Tông - HCM. (Có lời giải chi tiết)THPT Quốc giaVật lý

1 mã đề 39 câu hỏi 50 phút

5,991 lượt xem 3,192 lượt làm bài