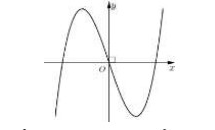
Đồ thị của hàm số nào dưới đây có dạng đường cong như hình bên

A.  

$y = x^{3} - 3 x .$

B.  

$y = - x^{4} + 2 x^{2} .$

C.  

$y = - x^{3} + 3 x .$

D.  

$y = - x^{4} - 2 x^{2} .$

Đáp án đúng là: A

Để xác định hàm số nào có đồ thị giống như hình bên, chúng ta cần xét các hàm số đã cho:

1. A.  $y = x^3 - 3x$
2. B.  $y = -x^4 + 2x^2$
3. C.  $y = -x^3 + 3x$
4. D.  $y = -x^4 - 2x^2$

Chúng ta cần vẽ sơ đồ đồ thị của các hàm số này để so sánh với hình vẽ.

Phân tích từng hàm số:

1.  $y = x^3 - 3x$

Đồ thị của hàm số này có dạng một đường cong bậc ba với các điểm cực trị. Tính đạo hàm để tìm các điểm cực trị:

$\frac{dy}{dx} = 3x^2 - 3$

Giải phương trình  $3x^2 - 3 = 0$ cho  $x = \pm 1$. Thay vào hàm số gốc để tìm y:

• Khi  $x = 1$,  $y = 1^3 - 3*1 = -2$
• Khi  $x = -1$,  $y = (-1)^3 - 3*(-1) = 2$

Điều này cho thấy hàm số này có hai điểm cực trị tại  $(1, -2)$ và  $(-1, 2)$. Đồ thị này khá phù hợp với hình vẽ.

2.  $y = -x^4 + 2x^2$

Hàm số này là một đa thức bậc bốn với hệ số âm trước  $x^4$, cho thấy đồ thị sẽ mở xuống. Đạo hàm:

$\frac{dy}{dx} = -4x^3 + 4x$

Giải phương trình  $-4x^3 + 4x = 0$ cho  $x = 0, \pm 1$. Thay vào hàm số gốc để tìm y:

• Khi  $x = 0$,  $y = 0$
• Khi  $x = 1$,  $y = -1 + 2 = 1$
• Khi  $x = -1$,  $y = -1 + 2 = 1$

Đồ thị này không có dạng như hình vẽ.

3.  $y = -x^3 + 3x$

Đồ thị của hàm số này cũng là một đường cong bậc ba nhưng khác với hàm số đầu tiên về dấu của hệ số. Đạo hàm:

$\frac{dy}{dx} = -3x^2 + 3$

Giải phương trình  $-3x^2 + 3 = 0$ cho  $x = \pm 1$. Thay vào hàm số gốc để tìm y:

• Khi  $x = 1$,  $y = -1 + 3 = 2$
• Khi  $x = -1$,  $y = 1 - 3 = -2$

Điều này cho thấy hàm số này cũng có hai điểm cực trị tại  $(1, 2)$ và  $(-1, -2)$. Đồ thị này cũng có thể là đáp án đúng nhưng không trùng khớp với hình vẽ vì dấu của các điểm cực trị ngược lại.

4.  $y = -x^4 - 2x^2$

Đây cũng là một đa thức bậc bốn với hệ số âm trước  $x^4$. Đạo hàm:

$\frac{dy}{dx} = -4x^3 - 4x$

Giải phương trình  $-4x^3 - 4x = 0$ cho  $x = 0, \pm \sqrt{-1}$. Phương trình này không có nghiệm thực ngoài x = 0.

Đồ thị này không có dạng như hình vẽ.

Kết luận:

Đồ thị của hàm số  $y = x^3 - 3x$ phù hợp nhất với hình vẽ.