Cho hàm số đa thức
có
và đồ thị hàm số
như hình vẽ.
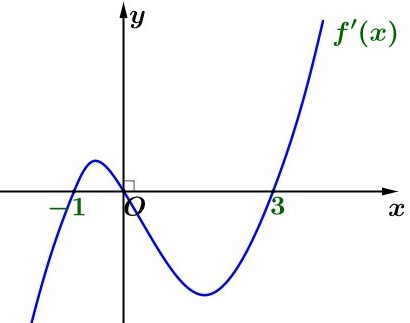
Số điểm cực trị của hàm số
là
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: A
Cho hàm số đa thức
có
và đồ thị hàm số
như hình vẽ.

Số điểm cực trị của hàm số là
.
.
.
.
Đáp án đúng là: A
Cho hàm số đa thức
có
và đồ thị hàm số
như hình vẽ.
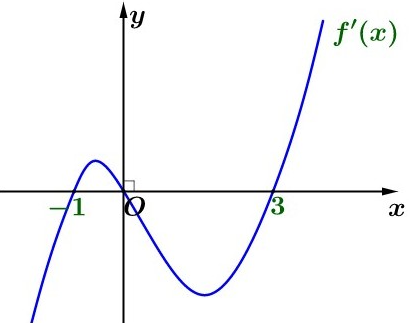
Số điểm cực trị của hàm số là
A. . B. . C. . D. .
Lời giải
Đặt
Cho và
+ Sử dụng công thức tính diện tích hình phẳng, ta có: .
BBT của hàm số
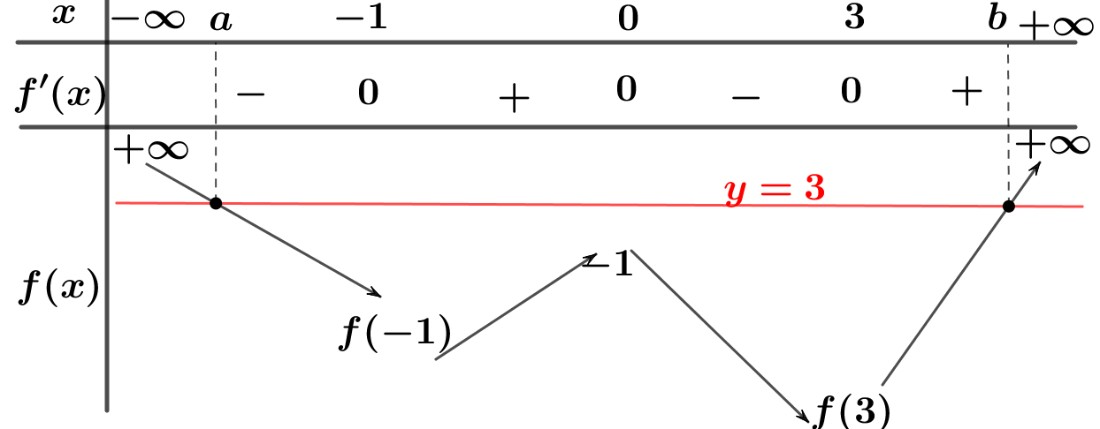
Sử dụng phương pháp ghép trục, ta có BBT của hàm số
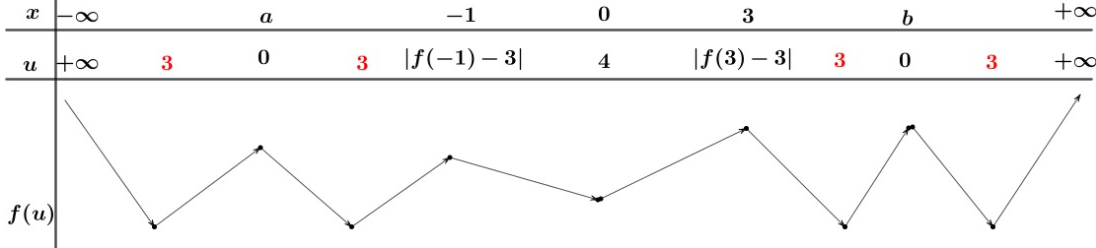
Vậy hàm số có 9 điểm cực trị.
Câu hỏi tương tự:
#7757 THPT Quốc giaToán
Cho hàm số đa thức có , với . Biết hàm số đồng biến trên khoảng và hàm số nghịch biến trên khoảng . Lập phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ , biết tiếp tuyến đi qua điểm ?
Lượt xem: 131,985 Cập nhật lúc: 08:57 14/05/2025
#7517 THPT Quốc giaToán
Cho
là hàm số đa thức bậc bốn và hàm số
có đồ thị là đường cong như hình dưới đây.
Hàm số có bao nhiêu điểm cực trị thuộc khoảng ?
Lượt xem: 127,889 Cập nhật lúc: 16:50 13/05/2025
#8590 THPT Quốc giaToán
Cho hai hàm đa thức
liên tục trên
, có đồ thị là hai đường cong như hình bên dưới. Biết rằng đồ thị hàm số
có đúng một cực trị là
, đồ thị hàm số
có đúng một điểm cực trị là
và
. Số giá trị nguyên của tham số
để hàm số
có đúng
điểm cực trị là.
Lượt xem: 146,145 Cập nhật lúc: 14:13 14/05/2025
#8828 THPT Quốc giaToán
Cho hàm số đa thức bậc bốn
thỏa mãn
và đồ thị hàm số
là đường cong trong hình vẽ.
Số điểm cực trị của hàm số là
Lượt xem: 150,223 Cập nhật lúc: 06:33 13/05/2025
#8621 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên sau
Hàm số đã cho đạt cực tiểu tại
Lượt xem: 146,664 Cập nhật lúc: 00:04 16/05/2025
#8993 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau:
Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
Lượt xem: 153,555 Cập nhật lúc: 05:14 15/05/2025
#7889 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 134,327 Cập nhật lúc: 20:59 16/05/2025
#8782 THPT Quốc giaToán
Cho hàm số
có bảng xét dấu đạo hàm như sau
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 149,459 Cập nhật lúc: 19:16 16/05/2025
#8814 THPT Quốc giaToán
Cho hàm số
có bảng biến thiên
Đồ thị hàm số đã cho có tiệm cận đứng là
Lượt xem: 150,004 Cập nhật lúc: 10:15 15/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
556 xem29 thi
