Cho hàm số
. Đồ thị của hàm số
trên đoạn
như hình vẽ (phần cong của đồ thị là một phần của parabol
). Biết
, giá trị của
bằng
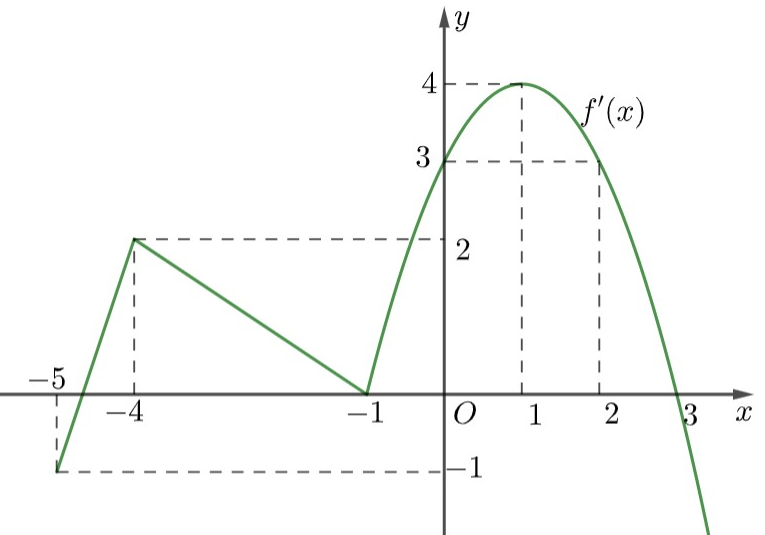
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: B
Cho hàm số
. Đồ thị của hàm số
trên đoạn
như hình vẽ (phần cong của đồ thị là một phần của parabol
). Biết
, giá trị của
bằng

.
.
.
.
Đáp án đúng là: B
Cho hàm số
. Đồ thị của hàm số
trên đoạn
như hình vẽ (phần cong của đồ thị là một phần của parabol
). Biết
, giá trị của
bằng
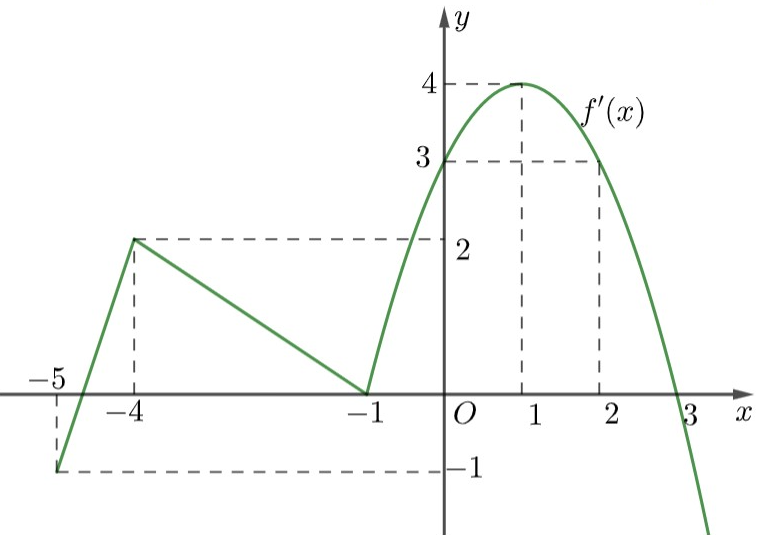
A. . B. . C. . D. .
Lời giải
Kí hiệu các điểm như hình vẽ.
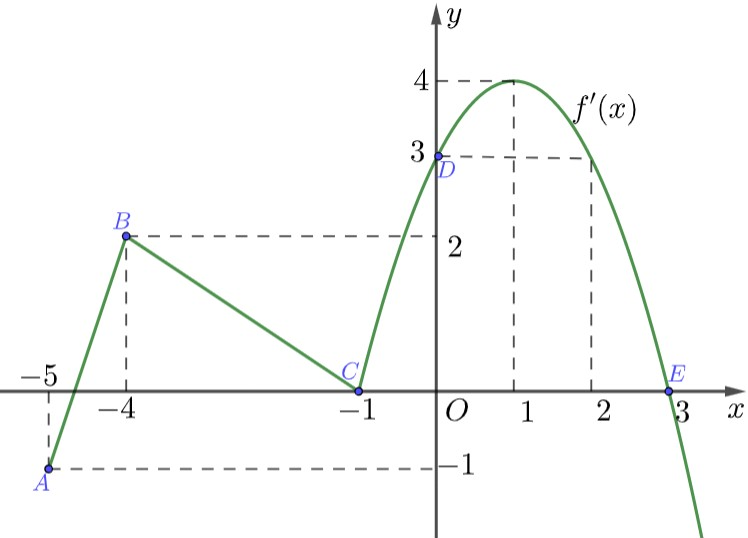
Đường thẳng đi qua hai điểm và nên có phương trình .
Đường thẳng đi qua hai điểm và nên có phương trình .
Parabol đi qua các điểm , , nên ta có hệ phương trình
.
Do đó .
Ta có .
Vì nên .
Lại có .
Vì nên .
Vậy .
Câu hỏi tương tự:
#8248 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên đoạn
và đồ thị như hình vẽ bên. Giá trị nhỏ nhất của hàm số trên đoạn
là:
Lượt xem: 140,332 Cập nhật lúc: 23:12 16/05/2025
#8665 THPT Quốc giaToán
Cho hàm số
, đồ thị hàm số
là đường cong trong hình vẽ dưới đây. Giá trị lớn nhất của hàm số
trên đoạn
bằng
Lượt xem: 147,451 Cập nhật lúc: 18:18 13/05/2025
#8112 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có đồ thị trên đoạn
như hình vẽ bên. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
trên đoạn
bằng
Lượt xem: 138,017 Cập nhật lúc: 07:38 17/05/2025
#7550 THPT Quốc giaToán
Cho hàm số
có đồ thị trên đoạn
như hình vẽ. Tìm giá trị lớn nhất
của hàm số
trên đoạn
.
Lượt xem: 128,457 Cập nhật lúc: 04:09 16/05/2025
#7522 THPT Quốc giaToán
Cho hàm số bậc ba
có đồ thị là đường cong đậm trong hình vẽ và đồ thị hàm số
với
có đồ thị là đường cong mảnh như hình vẽ. Đồ thị hàm số
có trục đối xứng là đường thẳng
. Tìm giá trị lớn nhất của hàm số
trên đoạn
.
Lượt xem: 128,008 Cập nhật lúc: 21:49 16/05/2025
#11376 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có đồ thị như hình vẽ bên dưới. Gọi
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
. Ta có
bằng:
Lượt xem: 193,544 Cập nhật lúc: 04:41 14/05/2025
#7596 THPT Quốc giaToán
Cho hàm số
có đồ thị là đường cong trong hình vẽ dưới đây. Giá trị lớn nhất của hàm số đã cho trên đoạn
bằng bao nhiêu ?
Lượt xem: 129,243 Cập nhật lúc: 16:44 16/05/2025
#7949 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình trên đoạn làLượt xem: 135,242 Cập nhật lúc: 07:32 17/05/2025
#8837 THPT Quốc giaToán
Hàm số bậc ba
có đồ thị như hình vẽ. Giá trị lớn nhất của hàm số đã cho trên đoạn
là
Lượt xem: 150,331 Cập nhật lúc: 04:47 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
1,461 xem100 thi
