Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8665

Cho hàm số f(x)f \left( x \right), đồ thị hàm số y=f′(x)y = f ' \left( x \right) là đường cong trong hình vẽ dưới đây. Giá trị lớn nhất của hàm số y=f(x4)+x2y = f \left( \dfrac{x}{4} \right) + \dfrac{x}{2} trên đoạn [−10; 6]\left[\right. - 10 ; \textrm{ } 6 \left]\right. bằng

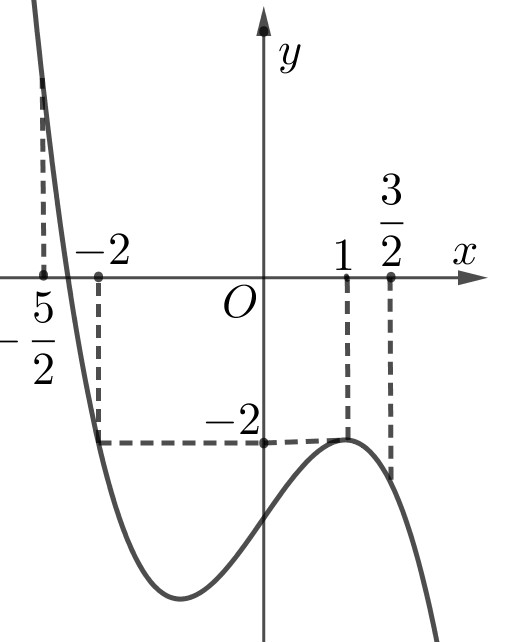
Hình ảnh


A.  

f(1)+2f \left( 1 \right) + 2.

B.  

f(1)f \left( 1 \right).

C.  

f(−2)−4f \left( - 2 \right) - 4.

D.  

f(−2)−1f \left( - 2 \right) - 1.

Đáp án đúng là: C

Cho hàm số f(x)f \left( x \right), đồ thị hàm số y=f′(x)y = f ' \left( x \right) là đường cong trong hình vẽ dưới đây. Giá trị lớn nhất của hàm số y=f(x4)+x2y = f \left( \dfrac{x}{4} \right) + \dfrac{x}{2} trên đoạn [−10; 6]\left[\right. - 10 ; \textrm{ } 6 \left]\right. bằng



A. f(1)+2f \left( 1 \right) + 2. B. f(1)f \left( 1 \right). C. f(−2)−4f \left( - 2 \right) - 4. D. f(−2)−1f \left( - 2 \right) - 1.
Lời giải
Đặt g(x)=f(x4)+x2g \left( x \right) = f \left( \dfrac{x}{4} \right) + \dfrac{x}{2}.
Ta có, g′(x)=14f′(x4)+12=0⇔f′(x4)=−2⇔[x4=−2x4=1   ⇔[x=−8x=4g ' \left( x \right) = \dfrac{1}{4} f ' \left( \dfrac{x}{4} \right) + \dfrac{1}{2} = 0 \Leftrightarrow f ' \left( \dfrac{x}{4} \right) = - 2 \Leftrightarrow \left[\right. \dfrac{x}{4} = - 2 \\ \dfrac{x}{4} = 1 \textrm{ }\textrm{ }\textrm{ } \Leftrightarrow \left[\right. x = - 8 \\ x = 4 trong đó x=4x = 4 là nghiệm bội chẵn.



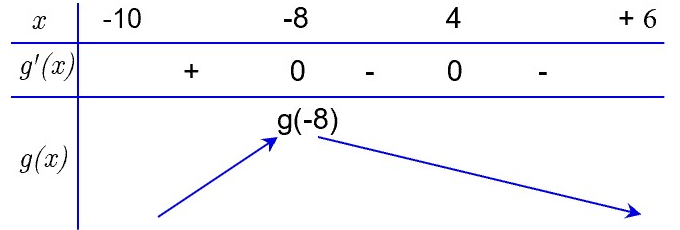
Dựa vào BBT ta có giá trị lớn nhất của hàm g(x)g \left( x \right) trên đoạn bằng .


 

Câu hỏi tương tự:

#8828 THPT Quốc giaToán

Cho hàm số đa thức bậc bốn y=f(x)y = f \left( x \right) thỏa mãn f(0)=−3f \left( 0 \right) = - 3 và đồ thị hàm số y=f′(x)y = f^{'} \left( x \right) là đường cong trong hình vẽ.



Số điểm cực trị của hàm số p(x)=f′(f(x)+x)p \left( x \right) = f^{'} \left(\right. f \left( x \right) + x \left.\right) là

Lượt xem: 150,174 Cập nhật lúc: 02:22 23/02/2025

#8817 THPT Quốc giaToán

Cho hàm số bậc năm y=f(x)y = f \left( x \right) và đồ thị hàm số y=f′(x)y = f^{'} \left( x \right) là đường cong trong hình vẽ dưới đây



Xét hàm số g(x)=3f(−x3−x+m+3)+(x3+x−m−3)(x3+x−m)2,mg \left( x \right) = 3 f \left( - x^{3} - x + m + 3 \right) + \left( x^{3} + x - m - 3 \right) \left( x^{3} + x - m \right)^{2} , m là tham số. Số giá trị nguyên của mm thuộc nửa khoảng (−100;100]\left(\right. - 100 ; 100 \left]\right. để hàm số g(x)g \left( x \right) đồng biến trên khoảng (0;3)\left( 0 ; 3 \right) là

Lượt xem: 150,056 Cập nhật lúc: 06:11 23/02/2025

#8790 THPT Quốc giaToán

Cho hàm số bậc ba y=f(x)y = f \left( x \right) có đồ thị là đường cong trong hình bên



Số điểm cực trị của hàm số g(x)=2f(x)g \left( x \right) = 2 f \left( x \right)là

Lượt xem: 149,486 Cập nhật lúc: 22:59 22/02/2025

#8776 THPT Quốc giaToán

Cho hàm số bậc ba y=f(x)y = f \left( x \right) có đồ thị là đường cong trong hình vẽ sau:



Số điểm cực trị của hàm số là

Lượt xem: 149,261 Cập nhật lúc: 23:02 22/02/2025

#7522 THPT Quốc giaToán

Cho hàm số bậc ba y=f(x)y = f \left( x \right) có đồ thị là đường cong đậm trong hình vẽ và đồ thị hàm số g(x)=f(ax2+bx+c)g \left( x \right) = f \left( a x^{2} + b x + c \right) với a,b,c∈Qa , b , c \in \mathbb{Q} có đồ thị là đường cong mảnh như hình vẽ. Đồ thị hàm số y=g(x)y = g \left( x \right) có trục đối xứng là đường thẳng x=−12x = - \dfrac{1}{2}. Tìm giá trị lớn nhất của hàm số g(x)g \left( x \right)trên đoạn [−2;2]\left[\right. - 2 ; 2 \left]\right..


Lượt xem: 127,948 Cập nhật lúc: 23:09 22/02/2025

#11374 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) có đạo hàm trên R\mathbb{R}và hàm số y=f′(x)y = f^{'} \left( x \right)là hàm số bậc ba có đồ thị là đường cong trong hình vẽ.



Hàm số y=f(x)y = f \left( x \right)nghịch biến trên

Lượt xem: 193,458 Cập nhật lúc: 23:19 22/02/2025

#8444 THPT Quốc giaToán

Cho hàm số y=ax+bcx+dy = \dfrac{a x + b}{c x + d} có đồ thị là đường cong trong hình vẽ bên. Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là

Lượt xem: 143,651 Cập nhật lúc: 06:34 23/02/2025

#11153 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) có đồ thị là đường cong trong hình vẽ dưới đây:



Tọa độ giao điểm của đồ thị hàm số đã cho và trục tung là:

Lượt xem: 189,690 Cập nhật lúc: 06:09 23/02/2025

#7917 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) có đồ thị là đường cong trong hình bên dưới.



Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

Lượt xem: 134,681 Cập nhật lúc: 16:32 22/02/2025


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN -THPT CHUYÊN LƯƠNG VĂN CHÁNH - PHÚ YÊN LẦN 1 (Bản word kèm giải)THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

1,291 lượt xem 644 lượt làm bài