Cho khối chóp $S . A B C D$ có đáy là hình vuông cạnh $a$ , $S A$ vuông góc với mặt phẳng đáy và $S C$ tạo với mặt phẳng đáy một góc bằng $\left(60\right)^{0}$ .Thể tích của khối chóp đã cho bằng
A.
$\sqrt{6} a^{3}$ .
B.
$\dfrac{\sqrt{6} a^{3}}{6}$ .
C.
$\dfrac{\sqrt{6} a^{3}}{3}$ .
D.
$\dfrac{\sqrt{6} a^{3}}{9}$ .
Đáp án đúng là: C

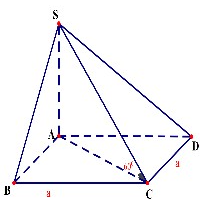
Ta có:

S A \bot \left( A B C D \right) \Rightarrow \left(\right. S C , \left( A B C D \right) \left.\right) = \left( S C , A C \right) = \widehat{S C A} = 60 \circ

A C = a \sqrt{2} ; S A = A C tan60 \circ = a \sqrt{6}

.
Thể tích khối chóp

S . A B C D

V = \dfrac{1}{3} S_{A B C D} . S A = \dfrac{1}{3} . a^{2} . a \sqrt{6} = \dfrac{a^{3} \sqrt{6}}{3}

Câu hỏi tương tự:

#11394 THPT Quốc giaToán

Cho khối chóp $S . A B C D$ có đáy là hình vuông cạnh $a ,$ cạnh bên $S A = y \textrm{ }\textrm{ } \left( y > 0 \right) .$ và vuông góc với mặt phẳng đáy $\left( A B C D \right)$ . Trên cạnh $A D$ lấy điểm $M$ và đặt $A M = x \textrm{ } \left( 0 < x < a \right) .$ Tính thể tích lớn nhất $V_{max}$ của khối chóp $S . A B C M ,$ biết $x^{2} + y^{2} = a^{2} .$

Lượt xem: 193,770 Cập nhật lúc: 07:39 17/01/2025

#8862 THPT Quốc giaToán

Cho khối chóp có đáy là hình vuông cạnh $a$ và chiều cao bằng $4 a$ . Thể tích khối chóp đã cho bằng

Lượt xem: 150,688 Cập nhật lúc: 02:50 18/01/2025

#8710 THPT Quốc giaToán

Cho khối chóp có đáy là hình vuông cạnh bằng $a$ và chiều cao bằng $3 a$ . Thể tích của khối chóp đã cho bằng

Lượt xem: 148,105 Cập nhật lúc: 01:30 17/01/2025

#8885 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy là hình vuông cạnh $a \sqrt{2}$ và chiều cao bằng $2 a$ . Thể tích của khối chóp $S . A B C D$ bằng:

Lượt xem: 151,130 Cập nhật lúc: 12:54 16/01/2025

#7668 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình vuông cạnh $2 a$ và $S A$ vuông góc với đáy. Góc giữa $S C$ và đáy bằng $\left(45\right)^{@}$ . Thể tích khối chóp $S . A B C D$ bằng.

Lượt xem: 130,395 Cập nhật lúc: 18:07 17/01/2025

#7741 THPT Quốc giaToán

Cho hình chóp có đáy là hình vuông cạnh $a$ và chiều cao bằng $4 a$ . Thể tích khối chóp đã cho bằng

Lượt xem: 131,630 Cập nhật lúc: 00:39 06/01/2025

#8923 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình vuông cạnh $a$ . Biết $S A \bot \left( A B C D \right)$ và $S A = a \sqrt{3}$ . Thể tích của khối chóp $S . A B C D$ là:

Lượt xem: 151,790 Cập nhật lúc: 18:28 18/01/2025

#8334 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy là hình vuông $A B C D$ cạnh $a$ , cạnh bên $S A$ vuông góc với mặt phẳng đáy và $S A = a \sqrt{2}$ . Thể tích của khối chóp $S . A B C D$ là

Lượt xem: 141,763 Cập nhật lúc: 18:33 18/01/2025

#8376 THPT Quốc giaToán

Cho hình chóp $S . A B C D$ có đáy là hình vuông cạnh $a$ , mặt bên $S A B$ nằm trong mặt phẳng vuông góc với $\left( A B C D \right)$ , $\widehat{S A B} = \left(30\right)^{0}$ , $S A = 2 a$ . Tính thể tích $V$ của khối chóp $S . A B C D .$

Lượt xem: 142,476 Cập nhật lúc: 01:08 17/01/2025

Đề thi chứa câu hỏi này:

61 . Đề thi thử TN THPT môn Toán năm 2024 - SỞ GIÁO DỤC YÊN BÁI - LẦN 1THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,497 lượt xem 2,359 lượt làm bài

LetQA - Nền tảng trắc nghiệm & đề thi đa lĩnh vực

Về chúng tôi

LetQA là công cụ hỗ trợ học sinh, sinh viên, giáo viên, tổ chức trong việc ôn luyện, kiểm tra kiến thức; được cung cấp miễn phí cho tất cả người dùng.
LetQA không cung cấp dịch vụ mạng xã hội, không cung cấp thông tin tổng hợp và không thu phí người dùng.

Thông tin liên hệ & hỗ trợ

Email: hotro@letqa.com

Facebook: Let QA (fb.com/letqavn)

Liên kết phổ biến

Yêu cầu bổ sung đề thi

Đóng góp đề thi

Website liên kết

Phần mềm kiểm tra trùng lặp Kiểm Tra Tài Liệu

Phần mềm xuất bản tạp chí điện tử VOJS

Công cụ kiểm tra chính tả và thể thức Viver

Công cụ hỗ trợ trích dẫn và phân tích khoa học Scholar Hub