Trong các điểm dưới đây, điểm nào thuộc đồ thị của hàm số
?
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: D
Trong các điểm dưới đây, điểm nào thuộc đồ thị của hàm số ?
.
.
.
.
Đáp án đúng là: D
(VD):
Phương pháp:
Chứng minh
.
Dựng khoảng cách từ
đến
.
Đặt
, sử dụng hệ thức lượng trong tam giác vuông tìm x theo a.
Tính thể tích
.
Cách giải:
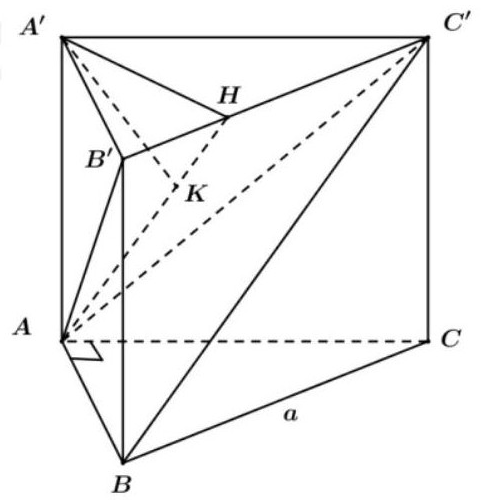
Vì BC // nên .
Trong kẻ , trong kẻ . Khi đó ta có:
Đặt . Áp dụng hệ thức lượng trong tam giác vuông ta có:
Khi đó ta có
Vậy .
Câu hỏi tương tự:
#11026 THPT Quốc giaSinh học
Hệ mạch của thú có bao nhiêu đặc điểm trong số các đặc điểm dưới đây?
I. Máu ở động mạch chủ giàu O2 II. Máu ở động mạch phổi nghèo CO2
III. Máu ở tĩnh mạch chủ giàu O2 IV. Máu ở tĩnh mạch phổi giàu O2
Lượt xem: 187,594 Cập nhật lúc: 08:56 14/05/2025
#470 THPT Quốc giaVật lý
Hình bên cho thấy pít-tông của một động cơ ô tô dao động trong xilanh làm cho trục khuỷu quay tròn. Khi cài số 1, bánh xe quay chậm hơn trục khuỷu 8 lần nhờ hệ thống bánh răng. Coi pít-tông dao động điều hòa trên hành trình dài từ điểm chết dưới đến điểm chết trên và bánh xe thuộc loại 215/55R17, tức có đường kính 17 in . Ở số 1 nói trên, khi tốc độ của xe là thì gia tốc của pít-tông ở các điểm chết bằng bao nhiêu?
Lượt xem: 8,169 Cập nhật lúc: 04:38 14/05/2025
#5221 THPT Quốc giaVật lý
Gọi , I là các điểm trên một lò xo nhẹ, được treo thẳng đứng ở điểm cố định. Khi lò xo có chiều dài tự nhiên thì . Gắn vật nhỏ vào đầu dưới của lò xo và kích thích đề vật dao động điều hòa theo phương thẳng đứng. Trong quá trình dao động tỉ số độ lớn lực kéo lớn nhất và độ lớn lực kéo nhỏ nhất tác dụng lên bằng 3; lò xo giãn đều; khoảng cách lớn nhất giữa hai điểm và là . Lấy . Vật dao động với tần số là:
Lượt xem: 88,854 Cập nhật lúc: 06:47 13/05/2025
#2695 THPT Quốc giaVật lý
Gọi M, N, I là các điểm trên một lò xo nhẹ, được treo thẳng đứng ở điểm cố định. Khi lò xo có chiều dài tự nhiên thì . Gắn vật nhỏ vào đầu dưới của lò xo và kích thích để vật dao động điều hòa theo phương thẳng đứng. Trong quá trình dao động, tỉ số độ lớn lực kéo lớn nhất và độ lớn lực kéo nhỏ nhất tác dụng lên bằng 3; lò xo dãn đều, khoảng cách lớn nhất giữa hai điểm là . Lấy . Vật dao động với tần số
Lượt xem: 45,906 Cập nhật lúc: 08:28 13/05/2025
#1335 THPT Quốc giaVật lý
Hình bên cho thấy pít-tông của một động cơ xe ô tô nhỏ dao động trong xi-lanh với chuyển động như một dao động điều hòa. Khối lượng của pít-tông là . Hành trình từ điểm chết dưới lên đến điểm chết trên của pít-tông là . Khi gia tốc cực đại lực tác dụng lên pít-tông là . Chuyển động quay của trục khuỷu có cùng chu kì với pít-tông nhưng khi dẫn qua hệ thống các bánh răng thì tốc độ quay của các bánh xe lúc này giảm 8 lần so với tốc độ quay của trục khuỷu. Bánh xe có đường kính . Tốc độ của xe ô tô là
Lượt xem: 22,880 Cập nhật lúc: 00:34 15/05/2025
#11028 THPT Quốc giaSinh học
Trong các đặc điểm sau đây có bao nhiêu đặc điểm đặc trưng cho loài có tốc độ tăng trưởng quần thể chậm
I. Kích thước cơ thể lớn
II. Tuổi thọ cao
III. Tuổi sinh sản lần đầu đến sớm
IV. Dễ bị ảnh hưởng bởi nhân tố sinh thái vô sinh của môi trường
Lượt xem: 187,572 Cập nhật lúc: 04:36 14/05/2025
#8277 THPT Quốc giaToán
Cho hình thang vuông tại và có , và với . Gọi , lần lượt là thể tích các khối tròn xoay tạo thành khi quay hình thang (kể cả các điểm trong) quanh đường thẳng và . Tìm để .
Lượt xem: 140,863 Cập nhật lúc: 23:04 12/05/2025
#8345 THPT Quốc giaToán
Trong không gian , cho các điểm . Tìm giá trị dương của để khối tứ diện có thể tích bằng .
Lượt xem: 142,027 Cập nhật lúc: 20:16 14/05/2025
#8834 THPT Quốc giaToán
Trong không gian , cho các điểm . Gọi là điểm nằm trên mặt phẳng sao cho đạt giá trị nhỏ nhất. Khi đó bằng
Lượt xem: 150,263 Cập nhật lúc: 06:30 14/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
5,142 xem384 thi
