Trong không gian $O x y z$, cho hai điểm $A \left( 2 ; 1 ; 3 \right)$, $B \left( 6 ; 5 ; 5 \right)$. Xét khối nón $\left( N \right)$ ngoại tiếp mặt cầu đường kính $A B$ có $B$ là tâm đường tròn đáy khối nón. Gọi $S$ là đỉnh của khối nón $\left( N \right)$. Khi thể tích khối nón $\left( N \right)$ nhỏ nhất thì mặt phẳng qua đỉnh $S$ và song song với mặt phẳng chứa đường tròn đáy của $\left( N \right)$ có phương trình $2 x + b y + c z + d = 0$. Tính $T = b + c + d$.

A.  

$T = 12$.

B.  

$T = 18$.

C.  

$T = 24$.

D.  

$T = 36$.

Đáp án đúng là: A

Trong không gian $O x y z$, cho hai điểm $A \left( 2 ; 1 ; 3 \right)$, $B \left( 6 ; 5 ; 5 \right)$. Xét khối nón $\left( N \right)$ ngoại tiếp mặt cầu đường kính $A B$ có $B$ là tâm đường tròn đáy khối nón. Gọi $S$ là đỉnh của khối nón $\left( N \right)$. Khi thể tích khối nón $\left( N \right)$ nhỏ nhất thì mặt phẳng qua đỉnh $S$ và song song với mặt phẳng chứa đường tròn đáy của $\left( N \right)$ có phương trình $2 x + b y + c z + d = 0$. Tính $T = b + c + d$.
A. $T = 12$. B. $T = 18$. C. $T = 24$. D. $T = 36$.
Lời giải
Mặt cầu $\left( S \right)$ đường kính $A B$ có tâm $I \left( 4 ; 3 ; 4 \right)$, bán kính $R = \dfrac{A B}{2} = 3$.
Giả sử thiết diện qua trục hình nón là tam giác $S M N$.

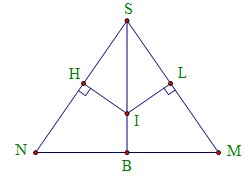
Gọi $r$, $h$ lần lượt là bán kính đáy và chiều cao của hình nón (

).
$I$ là tâm đường tròn nội tiếp của tam giác $S M N$ ta có: $R = \dfrac{S_{S M N}}{P_{S M N}}$
$\Rightarrow 3 = \dfrac{\dfrac{1}{2} M N . S B}{\dfrac{1}{2} \left( S M + S N + M N \right)}$
$\Leftrightarrow 3 = \dfrac{r . h}{r + \sqrt{r^{2} + h^{2}}}$
$\Leftrightarrow 3 \left( r + \sqrt{r^{2} + h^{2}} \right) = r h$
$\Leftrightarrow r^{2} = \dfrac{9 h}{h - 6}$.
Thể tích khối nón là $V = \dfrac{1}{3} \pi r^{2} h = \dfrac{\pi}{3} . \dfrac{9 h^{2}}{h - 6} = f \left( h \right)$.
$f^{'} \left( h \right) = 3 \pi . \dfrac{h^{2} - 12 h}{\left(\left( h - 6 \right)\right)^{2}}$.
$f^{'} \left( h \right) = 0 \Leftrightarrow \left[ h = 0 \\ h = 12 .$
Bảng biến thiên

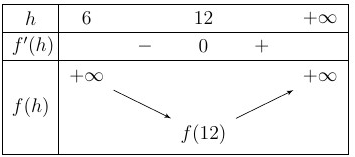
$V$ đạt giá trị nhỏ nhất $\Leftrightarrow h = 12$.
Ta có $\overset{\rightarrow}{I S} = 3 \overset{\rightarrow}{B I} \Rightarrow S \left(\right. - 2 ; - 3 ; 1 \right)$.
Phương trình mặt phẳng $\left( P \right)$ qua $S \left( - 2 ; - 3 ; 1 \right)$, có vec-tơ pháp tuyến $\overset{\rightarrow}{A B} = 2 \left( 2 ; 2 ; 1 \right)$ là $2 x + 2 y + z + 9 = 0$.
Suy ra

;

;

. Vậy $T = b + c + d = 12$.