Trang chủ Đề thi THPT Quốc gia Toán 16146
thumbnail

[2021] Trường THPT Tôn Đức Thắng - Đề thi thử THPT QG năm 2021 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2021 của Trường THPT Tôn Đức Thắng, miễn phí với đáp án đầy đủ. Đề thi được biên soạn bám sát cấu trúc chuẩn của Bộ Giáo dục, giúp học sinh luyện tập hiệu quả các dạng bài như hàm số, tích phân, và bài toán thực tế.

Từ khoá: Toán học hàm số tích phân bài toán thực tế năm 2021 Trường THPT Tôn Đức Thắng đề thi thử đề thi có đáp án

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯

Số câu hỏi: 25 câuSố mã đề: 1 đềThời gian: 1 giờ

209,947 lượt xem 16,146 lượt làm bài


Bạn chưa làm đề thi này!!!

 

Xem trước nội dung:

Câu 1: 1 điểm

Tìm nghiệm của hệ phương trình {2x+y=4x+2z=1+22y+z=2+2.\left\{ \begin{array}{l}2x + y = 4\\x + 2z = 1 + 2\sqrt 2 \\y + z = 2 + \sqrt 2 .\end{array} \right.

A.  
(1;2;22)\left( {1;2;2\sqrt 2 } \right)
B.  
(2;0;2)\left( {2;0;\sqrt 2 } \right)
C.  
(−1;6;2)\left( { - 1;6;\sqrt 2 } \right)
D.  
(1;2;2)\left( {1;2;\sqrt 2 } \right)
Câu 2: 1 điểm

Cho bất phương trình \frac{{2018}}{{3 - x}} > 1,\,\,\,\,\left( 1 \right) . Một học sinh giải như sau

\left( 1 \right)\mathop \Leftrightarrow \limits^{\left( {\rm{I}} \right)} \frac{1}{{3 - x}} > \frac{1}{{2018}}\mathop \Leftrightarrow \limits^{\left( {{\rm{II}}} \right)} \left\{ \begin{array}{l}x e 3\\3 - x < 2018\end{array} \right.\mathop \Leftrightarrow \limits^{\left( {{\rm{III}}} \right)} \left\{ \begin{array}{l}x e 3\\x > - 2015\end{array} \right. .

Hỏi học sinh này giải sai ở bước nào?

A.  
(I)
B.  
(II)
C.  
(III)
D.  
(II) và (III)
Câu 3: 1 điểm

Cho \sin a=\frac{3}{5}, \cos a<0, \cos b=\frac{3}{4}, \sin b>0 . Hãy tính sin⁡(a−b)\sin \left( a-b \right) ?

A.  
−15(7+94) - \frac{1}{5}\left( {\sqrt 7 + \frac{9}{4}} \right)
B.  
−15(7−94)- \frac{1}{5}\left( {\sqrt 7 - \frac{9}{4}} \right)
C.  
15(7+94)\frac{1}{5}\left( {\sqrt 7 + \frac{9}{4}} \right)
D.  
15(7−94)\frac{1}{5}\left( {\sqrt 7 - \frac{9}{4}} \right)
Câu 4: 1 điểm

Cho a→\overrightarrow{a} và b→\overrightarrow{b} là hai véc-tơ cùng hướng và đều khác 0→\overrightarrow{0} . Trong các kết quả sau đây, hãy chọn kết quả đúng?

A.  
a→.b→=∣a→∣.∣b→∣\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|
B.  
a→.b→=0\overrightarrow a .\overrightarrow b = 0
C.  
a→.b→=−1\overrightarrow a .\overrightarrow b = - 1
D.  
a→.b→=−∣a→∣.∣b→∣\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|
Câu 5: 1 điểm

Cho hệ trục tọa độ (O;i→;j→)\left( O;\overrightarrow{i};\overrightarrow{j} \right) . Tìm tọa độ của véc-tơ i→\overrightarrow{i} .

A.  
i→=(1;0)\overrightarrow i = \left( {1;0} \right)
B.  
i→=(0;1)\overrightarrow i = \left( {0;1} \right)
C.  
i→=(−1;0)\overrightarrow i = \left( { - 1;0} \right)
D.  
i→=(0;0)\overrightarrow i = \left( {0;0} \right)
Câu 6: 1 điểm

Tìm giá trị lớn nhất của hàm số y=5−4sin⁡xy = \sqrt {5 - 4\sin x} .

A.  
1
B.  
2
C.  
3
D.  
4
Câu 7: 1 điểm

Với các chữ số 2,3,4,5,6 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau trong đó hai chữ số 2,3 không đứng cạnh nhau?

A.  
120
B.  
96
C.  
48
D.  
72
Câu 8: 1 điểm

Chọn ngẫu nhiên 5 viên bi từ hộp đựng 7 viên bi xanh và 3 viên bi đỏ. Tính xác suất để 5 viên bi được chọn có đúng 3 viên bi xanh.

A.  
712\frac{7}{{12}}
B.  
1112\frac{11}{{12}}
C.  
512\frac{5}{{12}}
D.  
112\frac{1}{{12}}
Câu 9: 1 điểm

Cho cấp số nhân (un)\left( {{u}_{n}} \right) có u1=2{{u}_{1}}=2 và công bội q=3. Tính u3{{u}_{3}} .

A.  
u3=8{u_3} = 8
B.  
u3=18{u_3} = 18
C.  
u3=5{u_3} = 5
D.  
u3=6{u_3} = 6
Câu 10: 1 điểm

Tính lim⁡x→+∞2x+1x−1\mathop {\lim }\limits_{x \to + \infty } \frac{{2x + 1}}{{x - 1}}

A.  
1
B.  
2
C.  
3
D.  
4
Câu 11: 1 điểm

Cho f(x)=x3−2x2+5f\left( x \right)={{x}^{3}}-2{{x}^{2}}+5 tính f′′(1){{f}'}'\left( 1 \right) ?

A.  
-3
B.  
2
C.  
4
D.  
-1
Câu 12: 1 điểm

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d:x-2y+3=0. Viết phương trình d' là ảnh của đường thẳng d qua phép tịnh tiến theo véc-tơ v→=(3 ;1)\overrightarrow{v}=(3\,;1) .

A.  
d':x - 2y + 2 = 0
B.  
d':x - 2y - 2 = 0
C.  
d':2x - y + 2 = 0
D.  
d':2x - y - 2 = 0
Câu 13: 1 điểm

Cho tứ diện ABCD, gọi M,  NM,\,\,N lần lượt là trung điểm của AD và BC. Khi đó, giao tuyến của mặt phẳng (MBC)\left( MBC \right) và (NDA)\left( NDA \right) là

A.  
AD
B.  
MN
C.  
AC
D.  
BC
Câu 14: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mệnh đề nào sau đây sai?

A.  
(SAB)∩(SAD)=SA\left( {SAB} \right) \cap \left( {SAD} \right) = SA
B.  
AD∣∣(SBC)AD||\left( {SBC} \right)
C.  
SA và CD chéo nhau
D.  
Giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song với AC.
Câu 15: 1 điểm

Cho tứ diện đều ABCD cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu?

A.  
30o
B.  
45o
C.  
60o
D.  
90o
Câu 16: 1 điểm

Tính diện tích S của tam giác có ba đỉnh là ba điểm cực trị của đồ thị hàm số f(x)=x4−2x2+3f\left( x \right) = {x^4} - 2{x^2} + 3 .

A.  
S = 2
B.  
S=12S = \frac{1}{2}
C.  
S = 4
D.  
S = 1
Câu 17: 1 điểm

Tính giá trị cực tiểu của hàm số y=x3−3x2+1y = {x^3} - 3{x^2} + 1

A.  
yCT=0{y_{{\rm{CT}}}} = 0
B.  
yCT=1{y_{{\rm{CT}}}} = 1
C.  
yCT=−3{y_{{\rm{CT}}}} = -3
D.  
yCT=2{y_{{\rm{CT}}}} = 2
Câu 18: 1 điểm

Tìm m để đồ thị hàm số y=x4−2mx2+1y={{x}^{4}}-2m{{x}^{2}}+1 có ba điểm cực trị A(0;1),B,CA\left( 0;1 \right),B,C sao cho BC=4.

A.  
m = - 4;m = 4
B.  
m=2m = \sqrt 2
C.  
m = 4
D.  
m=−2;m=2m = - \sqrt 2 ;m = \sqrt 2
Câu 19: 1 điểm

Tìm giá trị lớn nhất của tham số m để hàm số y=13x3−mx2+(4m−3)x+2018y = \frac{1}{3}{x^3} - m{x^2} + \left( {4m - 3} \right)x + 2018 đồng biến trên R.

A.  
m = 0
B.  
m = 1
C.  
m = 3
D.  
m = 4
Câu 20: 1 điểm

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x)=2x3−3x2−12x+10f\left( x \right)=2{{x}^{3}}-3{{x}^{2}}-12x+10 trên đoạn [−3;3]\left[ -3;3 \right] là

A.  
max⁡[−3;3]f(x)=1;min⁡[−3;3]f(x)=−35\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 1;\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = - 35
B.  
max⁡[−3;3]f(x)=1;min⁡[−3;3]f(x)=−10\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 1;\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = - 10
C.  
max⁡[−3;3]f(x)=17;min⁡[−3;3]f(x)=−10\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 17;\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = - 10
D.  
max⁡[−3;3]f(x)=17;min⁡[−3;3]f(x)=−35\mathop {\max }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = 17;\mathop {\min }\limits_{\left[ { - 3;3} \right]} f\left( x \right) = - 35
Câu 21: 1 điểm

Tìm tiệm cận đứng của đồ thị hàm số y=3−4xx+1y=\frac{3-4x}{x+1} .

A.  
x = 1
B.  
x = -1
C.  
y = 1
D.  
y = -1
Câu 22: 1 điểm

Cho hàm số y=f(x)y=f\left( x \right) có đồ thị như hình vẽ bên. Xác định m để phương trình ∣f(x)∣=m\left| f\left( x \right) \right|=m có 6 nghiệm thực phân biệt.

A.  
m > 4
B.  
0 < m < 4
C.  
0 < m < 3
D.  
3 < m < 4
Câu 23: 1 điểm

Cho hàm số y=f(x)=ax3+bx2+cx+dy = f\left( x \right) = a{x^3} + b{x^2} + cx + d có đồ thị như hình vẽ bên. Tính S = a + b.

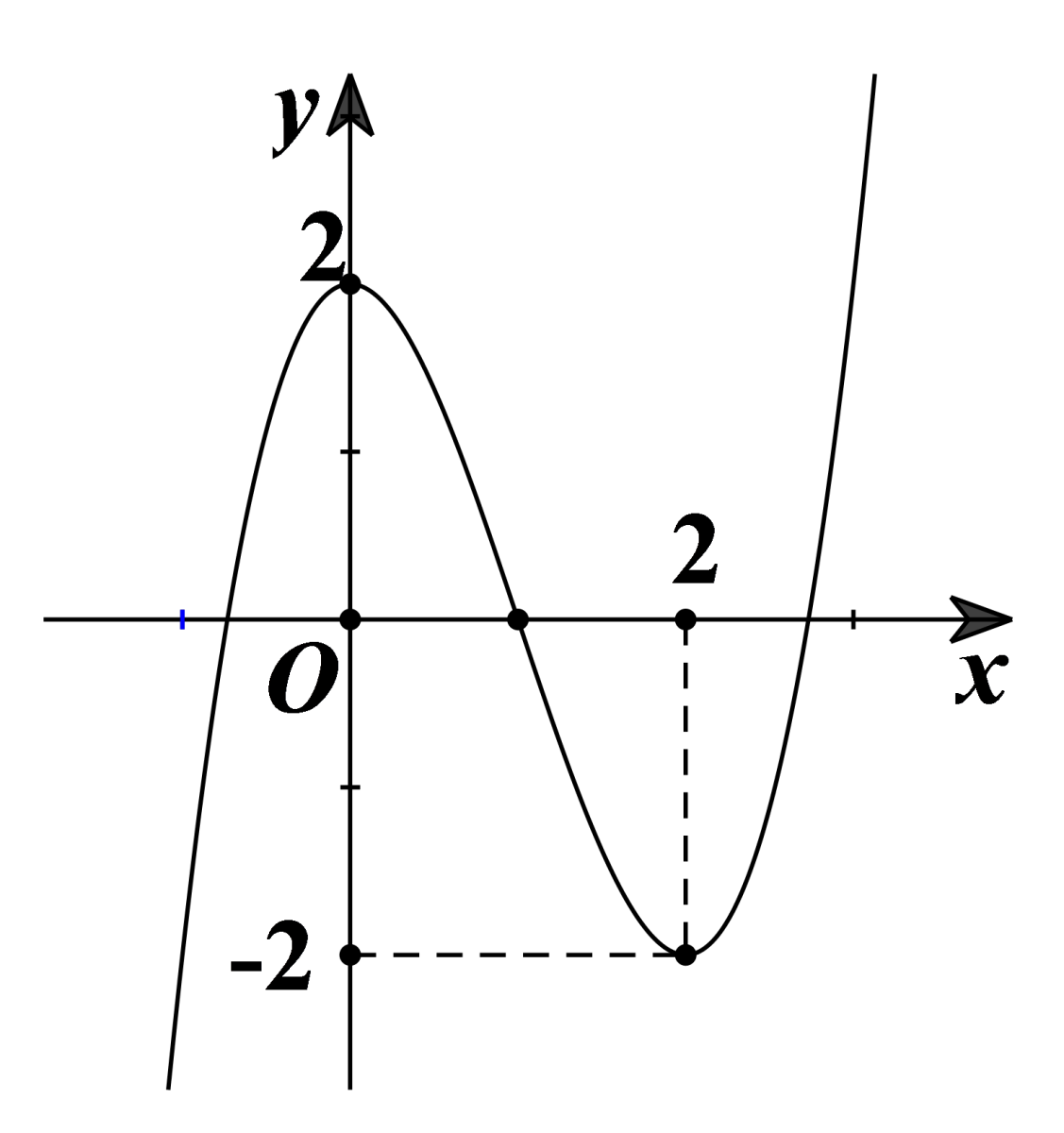
Hình ảnh

A.  
S = 1
B.  
S = 0
C.  
S = -2
D.  
S = -1
Câu 24: 1 điểm

Chọn khẳng định sai trong các khẳng định sau

A.  
log⁡13a>log⁡13b⇔a>b>0{\log _{\frac{1}{3}}}a > {\log _{\frac{1}{3}}}b \Leftrightarrow a > b > 0
B.  
log⁡3x<0⇔0<x<1{\log _3}x < 0 \Leftrightarrow 0 < x < 1
C.  
log⁡12a=log⁡12b⇔a=b>0{\log _{\frac{1}{2}}}a = {\log _{\frac{1}{2}}}b \Leftrightarrow a = b > 0
D.  
ln⁡x>0⇔x>1\ln x > 0 \Leftrightarrow x > 1
Câu 25: 1 điểm

Tìm mệnh đề đúng trong các mệnh đề sau

A.  
B.  
Hàm số y=log⁡axy={{\log }_{a}}x với 0

Đề thi tương tự

[2021] Trường THPT Lê Thánh Tôn - Đề thi thử THPT QG năm 2021 môn Sinh

1 mã đề 40 câu hỏi 1 giờ

212,482 xem16,341 thi

[2021] Trường THPT Vĩnh Bình - Đề thi thử THPT QG năm 2021 môn Sinh

1 mã đề 40 câu hỏi 1 giờ

214,620 xem16,505 thi

[2021] Trường THPT Duy Tân lần 2 - Đề thi thử THPT QG năm 2021 môn Sinh

1 mã đề 40 câu hỏi 1 giờ

213,302 xem16,404 thi

[2021] Trường THPT Bùi Hữu Nghĩa - Đề thi thử THPT QG năm 2021 môn Tiếng Anh

1 mã đề 50 câu hỏi 1 giờ

214,805 xem16,518 thi

[2021] Trường THPT Lê Đại Hành - Đề thi thử THPT QG năm 2021 môn Tiếng Anh

1 mã đề 50 câu hỏi 1 giờ

215,827 xem16,598 thi

[2021] Trường THPT Âu Cơ - Đề thi thử THPT QG năm 2021 môn Hóa học

1 mã đề 40 câu hỏi 1 giờ

221,861 xem17,062 thi

[2021] Trường THPT Ngô Quyền - Đề thi thử THPT QG năm 2021 môn Tiếng Anh

1 mã đề 50 câu hỏi 1 giờ

221,589 xem17,041 thi

[2021] Trường THPT Trần Hưng Đạo - Đề thi thử THPT QG năm 2021 môn Sinh

1 mã đề 40 câu hỏi 1 giờ

219,189 xem16,852 thi

[2021] Trường THPT Phan Bội Châu Lần 2 - Đề thi thử THPT QG năm 2021 môn Tiếng Anh

1 mã đề 50 câu hỏi 1 giờ

219,575 xem16,886 thi