52 câu trắc nghiệm: Khái niệm về mặt tròn xoay có đáp án

Chương 2: Mặt nón, mặt trụ, mặt cầu
Bài 1 : Khái niệm về mặt tròn xoay
Lớp 12;Toán

Thời gian làm bài: 1 giờ

Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!

Xem trước nội dung:

Câu 1: 1 điểm

Tam giác ABC vuông cân đỉnh A có cạnh huyền là a. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo thành hình nón (N). Diện tích xung quanh của hình nón (N) là:

A. $\frac{a^{2} \sqrt{2}}{4}$

B. $\frac{a^{2} \sqrt{2}}{2}$

C. $\frac{{πa}^{2} \sqrt{2}}{2}$

D. $\frac{{πa}^{2} \sqrt{2}}{4}$

Câu 2: 1 điểm

Hình nón (N) có đường sinh gấp hai lần bán kính đáy. Góc ở đỉnh của hình nón là:

120^o

60^o

30^o

0^o

Câu 3: 1 điểm

Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng:

\frac{2}{3}

\frac{1}{2}

1 + \frac{1}{\sqrt{5}}

\frac{\sqrt{5}}{1 + \sqrt{5}}

Câu 4: 1 điểm

Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được:

150720π(c $m^{3}$ )

50400π(c $m^{3}$ )

16000π(c $m^{3}$ )

12000π(c $m^{3}$ )

Câu 5: 1 điểm

Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là:

2π $a^{3}$

π $a^{3}$

2π $a^{3}$ /3

π $a^{3}$ /2

Câu 6: 1 điểm

Cho hình trụ có diện tích toàn phần là 7π $a^{2}$ và bán kính đáy là a. Chiều cao của hình trụ là:

3a/2

5a/3

5a/2

Câu 7: 1 điểm

Để làm một thùng phi hình trụ người ta cần hai miếng nhựa hình tròn làm hai đáy có diện tích mỗi hình là 4π(c $m^{2}$ ) và một miếng nhựa hình chữ nhật có diện tích là 15π(c $m^{2}$ ) để làm thân. Tính chiều cao của thùng phi được làm.

15/4(cm)

5(cm)

15/2(cm)

15(cm)

Câu 8: 1 điểm

Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)

1/4

1/2

Câu 9: 1 điểm

Cho hình trụ có bán kính đáy bằng a và diện tích toàn phần 6π $a^{2}$ . Diện tích của thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua các trục của hình trụ là:

$a^{2}$

2 $a^{2}$

4 $a^{2}$

6 $a^{2}$

Câu 10: 1 điểm

Cho khối trụ có diện tích toàn phần là π và có thiết diện cắt bởi mặt phẳng đi qua trục là hình vuông. Thể tích khối trụ là:

A. $\frac{4 π}{9}$

B. $\frac{π \sqrt{6}}{9}$

C. $\frac{π \sqrt{6}}{12}$

D. $\frac{π \sqrt{6}}{18}$

Câu 11: 1 điểm

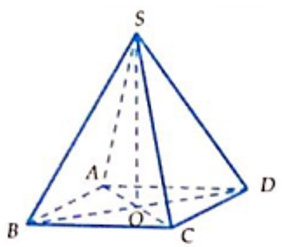
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a $\sqrt{2}$ . Tính thể tích V của khối nón có đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD?

V = \frac{{πa}^{3}}{2}

V = \frac{{πa}^{3} \sqrt{2}}{6}

V = \frac{{πa}^{3}}{6}

V = \frac{{πa}^{3} \sqrt{2}}{2}

Câu 12: 1 điểm

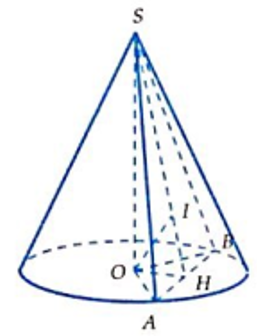
Cho hình nón S có chiều cao h = a và bán kính đáy r = 2a. Mặt phẳng (P) đi qua S và cắt đường tròn đáy tại A và B sao cho AB = 2 $\sqrt{3}$ a Tính khoảng cách d từ tâm của đường tròn đáy đến (P)

\frac{a \sqrt{3}}{2}

a

$\frac{a \sqrt{5}}{5}$

D. $\frac{a \sqrt{2}}{2}$

Câu 13: 1 điểm

Cho khối nón tròn xoay có bán kính đáy r, đường sinh l và đường cao h. Công thức tính thể tích khối nón là:

\frac{1}{3} {πr}^{2} l

\frac{1}{3} {πrh}^{2}

\frac{1}{3} {πr}^{2} h

{πr}^{2} h

Câu 14: 1 điểm

Hình nón (N) có đường sinh gấp hai lần đường cao. Góc ở đỉnh của hình nón là:

12 $0^{o}$

9 $0^{o}$

6 $0^{o}$

3 $0^{o}$

Câu 15: 1 điểm

Hình nón có chiều cao bằng 4/3 bán kính đáy. Tỉ số giữa diện tích toàn phần và diện tích xung quanh của hình nón là:

4/3

5/7

8/5

9/5

Câu 16: 1 điểm

Hình nón có góc ở đỉnh là 9 $0^{o}$ và có diện tích xung quanh là π $\sqrt{2}$ . Độ dài đường cao của hình nón là:

$\sqrt{2}$

1/ $\sqrt{2}$

Câu 17: 1 điểm

Cho hình nón tròn xoay có đường cao h=15cm và bán kính đáy r = 20cm. Diện tích xung quanh của hình nón là:

1000π(c $m^{2}$ )

250π(c $m^{2}$ )

375π(c $m^{2}$ )

500π(c $m^{2}$ )

Câu 18: 1 điểm

Cho khối nón tròn xoay có đường cao h = 20cm và đường sinh l = 25cm. Thể tích khối nón là:

1500π(c $m^{3}$ )

2500π(c $m^{3}$ )

3500π(c $m^{3}$ )

4500π(c $m^{3}$ )

Câu 19: 1 điểm

Tam giác ABC vuông đỉnh A có AB = 2AC. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo ra hình nón (N1) và quay tam giác ABC quanh trục AC thì đoạn gấp khúc ABC tạo ra hình nón (N2). Tỉ số diện tích xung quanh của hình nón (N1) và diện tích xung quanh của hình nón (N2) là:

1/4

1/2

Câu 20: 1 điểm

Cho khối nón tròn xoay có góc ở đỉnh là 60^o và đường sinh l = 6cm. Thể tích của khối nón là:

9π $\sqrt{3}$ (c $m^{3}$ )

27π $\sqrt{3}$ (c $m^{3}$ )

27π (c $m^{3}$ )

3π $\sqrt{3}$ (c $m^{3}$ )

Câu 21: 1 điểm

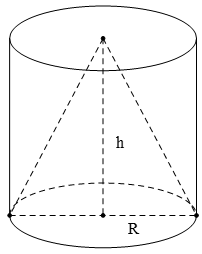
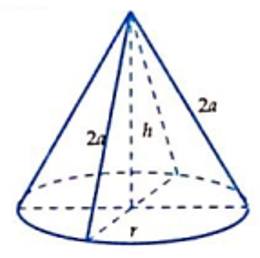
Cho một hình trụ có bán kính đáy R, chiều cao h và thể tích $V_{1}$ ; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích $V_{2}$ .

Khẳng định nào sau đây là khẳng định đúng ?

$V_{2}$ = 3 $V_{1}$

$V_{1}$ = 2 $V_{2}$

$V_{1}$ = 3 $V_{2}$

$V_{2}$ = $V_{1}$

Câu 22: 1 điểm

Khối nón có góc ở đỉnh là 6 $0^{o}$ và có thể tích là π. Độ dài đường sinh của khối nón là:

2 \sqrt[6]{3}

2 \sqrt[3]{9}

2 \sqrt[3]{3}

Câu 23: 1 điểm

Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.

\frac{{πa}^{3} \sqrt{2}}{16}

\frac{{πa}^{3} \sqrt{2}}{4}

\frac{{πa}^{3} \sqrt{2}}{2}

D. $\frac{3 {πa}^{3} \sqrt{2}}{16}$

Câu 24: 1 điểm

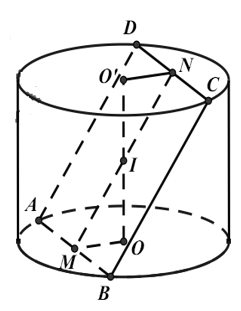
Cho khối trụ có bán kính đáy 4m và đường cao là 5m. Thể tích khối trụ là:

20π( $m^{3}$ )

60π( $m^{3}$ )

80π( $m^{3}$ )

100π( $m^{3}$ )

Câu 25: 1 điểm

Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:

6π $a^{2}$

3π $a^{2}$

2π $a^{2} \sqrt{3}$

π $a^{2} \sqrt{6}$

Câu 26: 1 điểm

Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).

48 π ({cm}^{3})

B. $24 π ({cm}^{3})$

72 π ({cm}^{3})

D. $18 π ({cm}^{3})$

Câu 27: 1 điểm

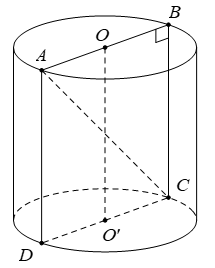
Cho hình trụ có diện tích toàn phần 6π $a^{2}$ và thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua trục là một hình vuông. Chiều cao của hình trụ là:

3a/4

3a/2

Câu 28: 1 điểm

Cho hình trụ có diện tích toàn phần là 12π, đường cao của hình trụ là 1. Diện tích xung quanh của hình trụ là:

6π

4π

2π

$π$

Câu 29: 1 điểm

Cho hình trụ có chiều cao bằng 2a và diện tích xung quanh là π $a^{2}$ . Bán kính đáy của hình trụ là:

\frac{3 a}{4}

B. $\frac{a}{2}$

C. $\frac{a}{3}$

D. $\frac{a}{4}$

Câu 30: 1 điểm

Cho khối trụ có diện tích toàn phần 5π $a^{2}$ và bán kính đáy là a. Thể tích khối trụ là:

3π $a^{3}$ /2

π $a^{3}$ /2

π $a^{3}$

3π $a^{3}$

Câu 31: 1 điểm

Hình trụ (H) có diện tích toàn phần là 8π(c $m^{2}$ ) và thể tích khối trụ là 3π(c $m^{3}$ ). Tính chiều cao của hình trụ ta được bao nhiêu kết quả?

C. 3

Câu 32: 1 điểm

Hình trụ (H) có tỉ số diện tích xung quanh và diện tích toàn phần là 1/3. Biết rằng thể tích khối trụ là 4π. Bán kính đáy của hình trụ là:

$\sqrt{6}$

$\sqrt{7}$

Câu 33: 1 điểm

Ta dùng hai hình chữ nhật có cùng kích cỡ để làm thành hai hình trụ (H1) và (H2) bằng cách quay các hình chữ nhật đó, lần lượt theo chiều dài và chiều rộng. Tỉ số hai diện tích xung quanh hình trụ (H1) và hình trụ (H2) là:

1/2

$\frac{1}{4}$

Câu 34: 1 điểm

Cho hình nón có đường cao h = 10cm và thiết diện cắt bởi mặt phẳng qua trục của hình nón là một tam giác đều. Diện tích xung quanh của hình nón là:

A. $200 π ({cm}^{2})$

B. $\frac{200 π}{3} ({cm}^{2})$

C. $\frac{400 π}{3} ({cm}^{2})$

D. $150 π ({cm}^{2})$

Câu 35: 1 điểm

Một hình nón có đường sinh bằng đường kính đáy. Diện tích xung quanh của hình nón bằng 9π. Tính đường cao h của hình nón.

\frac{3 \sqrt{6}}{2}

B. $\sqrt{3}$

C. $\frac{\sqrt{3}}{2}$

D. $\frac{\sqrt{3}}{3}$

Câu 36: 1 điểm

Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60°. Tính diện tích xung quanh S_xq của hình nón đỉnh S có đáy là hình tròn ngoại tiếp tam giác ABC.

\frac{{πa}^{2} \sqrt{3}}{3}

B. $\frac{{πa}^{2} \sqrt{10}}{8}$

C. $\frac{{πa}^{2} \sqrt{7}}{4}$

D. $\frac{{πa}^{2} \sqrt{7}}{6}$

Câu 37: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SC = a $\sqrt{6}$ . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:

\frac{4 {πa}^{3}}{3}

\frac{{πa}^{3} \sqrt{2}}{6}

C. $\frac{{πa}^{3} \sqrt{3}}{3}$

D. $\frac{{πa}^{3} \sqrt{6}}{3}$

Câu 38: 1 điểm

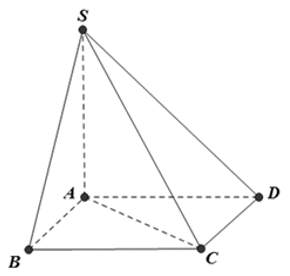
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = a, AB' = 2a. Diện tích toàn phần của hình trụ ngoại tiếp hình hộp là:

π $a^{2}$ (1 + $\sqrt{6}$ )

π $a^{2}$ (1 + $\sqrt{3}$ )

π $a^{2}$ (1 + $\sqrt{2}$ )

2π $a^{2}$

Câu 39: 1 điểm

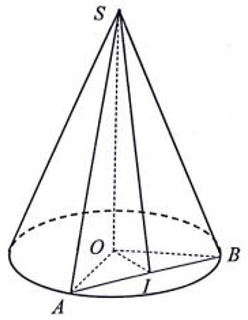
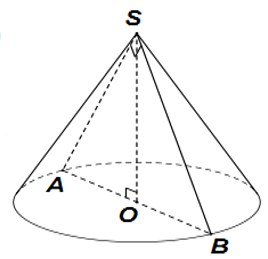
Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và . Tính diện tích xung quanh hình nón ?

4 π \sqrt{3}

B. $\frac{3 π \sqrt{2}}{4}$

C. $2 π \sqrt{3}$

D. $3 π \sqrt{2}$

Câu 40: 1 điểm

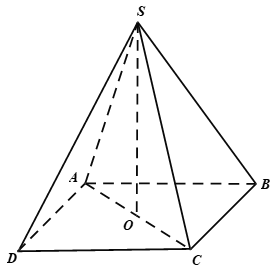
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc $\hat{SAB}$ = 60°. Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:

\frac{{πa}^{3} \sqrt{3}}{12}

B. $\frac{{πa}^{3} \sqrt{2}}{12}$

C. $\frac{{πa}^{3} \sqrt{2}}{6}$

D. $\frac{{πa}^{3} \sqrt{3}}{6}$

Câu 41: 1 điểm

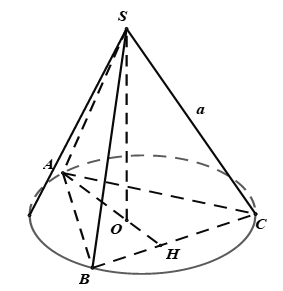
Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a, có diện tích xung quanh là:

\frac{{πa}^{2}}{3}

B. $\frac{{πa}^{2} \sqrt{2}}{3}$

C. $\frac{{πa}^{2} \sqrt{3}}{3}$

D. $\frac{{πa}^{2} \sqrt{3}}{6}$

Câu 42: 1 điểm

Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng

\frac{{πa}^{2}}{2}

$\frac{{πa}^{2} \sqrt{2}}{2}$

C. $\frac{3 {πa}^{2}}{2}$

D. ${πa}^{2}$

Câu 43: 1 điểm

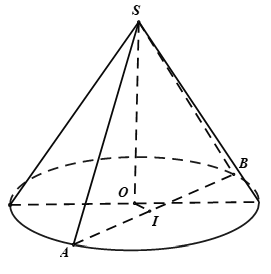
Cho hình nón S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và . Tính diện tích xung quanh hình nón.

\frac{3 {πa}^{2}}{2}

B. $\frac{{πa}^{2}}{2}$

C. $\frac{{πa}^{2} \sqrt{3}}{2}$

D. ${πa}^{2} \sqrt{3}$

Câu 44: 1 điểm

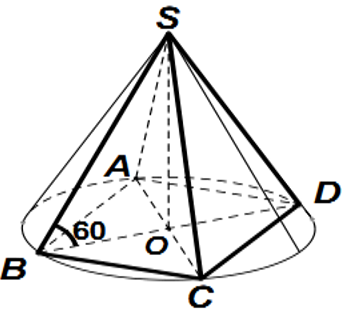
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng

A. $S_{xq} = {πa}^{2}; V = \frac{{πa}^{3} \sqrt{6}}{12}$

B. $S_{xq} = {πa}^{2}; V = \frac{{πa}^{3} \sqrt{3}}{12}$

C. $S_{xq} = 2 {πa}^{2}; V = \frac{{πa}^{3} \sqrt{3}}{12}$

D. $S_{xq} = 2 {πa}^{2}; V = \frac{{πa}^{3} \sqrt{6}}{6}$

Câu 45: 1 điểm

Một người xây nhà phải xây bốn cái cột hình trụ cùng kích cỡ, bán kính đáy các cột là 25cm. Biết rằng tổng thể tích vật liệu (chính là tổng thể tích bốn khối trụ) là 3 $m^{3}$ . Chiều cao của mỗi cột là:

\frac{π}{3} (m)

B. $\frac{10}{π} (m)$

C. $\frac{12}{π} (m)$

D. $\frac{15}{π} (m)$

Câu 46: 1 điểm

Một hộp đứng bóng bàn hình trụ có chiều cao 30cm, bán kính 2,5cm. Vận động viên để các quả bóng bàn có bán kính 2,5cm vao hộp. Hỏi vận động viên có thể để được nhiều nhất bao nhiêu quả bóng bàn trong các kết quả sau?

Câu 47: 1 điểm

Một hình nón có độ dài đường sinh bằng 2a và mặt phẳng qua trục cắt hình nón theo thiết diện là tam giác vuông. Tính thể tích V của khối nón.

\frac{2 {πa}^{3} \sqrt{2}}{3}

B. $\frac{{πa}^{3} \sqrt{3}}{3}$

C. $\frac{2 {πa}^{3} \sqrt{3}}{3}$

D. $\frac{{πa}^{3} \sqrt{2}}{3}$

Câu 48: 1 điểm

Cho hình trụ có bán kính đáy 10cm và đường cao là 15cm. ta để một thước thẳng có chiều dài l vào trong hình trụ. Khi đó trong các kết quả sau l có thể nhận giá trị lớn nhất là:

30 (cm)

25 (cm)

20(cm)

15(cm)

Câu 49: 1 điểm

Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60^o. Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được:

3 {πa}^{3}

B. ${πa}^{3}$

C. $\frac{4 {πa}^{3}}{3}$

D. $\frac{{πa}^{3}}{3}$

Câu 50: 1 điểm

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là:

\frac{{πa}^{3} \sqrt{6}}{4}

B. $\frac{{πa}^{3} \sqrt{3}}{3}$

\frac{{πa}^{3} \sqrt{6}}{6}

\frac{2 {πa}^{3} \sqrt{6}}{3}

Câu 51: 1 điểm

Cho hình chóp tứ giác đều S.ABCD có chiều cao SO = h = $\sqrt{3}$ và góc $\hat{SAB}$ = α = 60°. Tính diện tích xung quanh của hình nón đỉnh S đáy là đường tròn ngoại tiếp tứ giác ABCD

3 π \sqrt{2}

B. $3 π \sqrt{2}$

C. $6 π \sqrt{2}$

D. $8 π \sqrt{2}$

Câu 52: 1 điểm

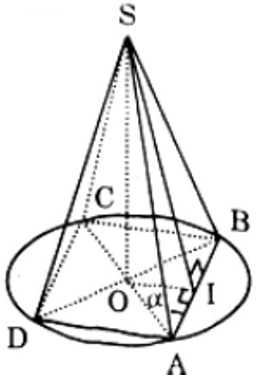
Cho hình trụ có đường cao h và bán kính đáy là r. Trong các khối lăng trụ tứ giác nội tiếp hình trụ thì khối lăng trụ có thể tích lớn nhất bằng:

A. h $r^{2}$

2h $r^{2}$

3h $r^{2}$

4h $r^{2}$

Xem thêm đề thi tương tự

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - CỤM GIA LỘC - HẢI DƯƠNG THPT Quốc giaToán

/Môn Toán/Đề thi thử Toán 2023 các trường, sở

50 câu hỏi 1 mã đề 1 giờ 30 phút

752 lượt xem 364 lượt làm bài