Bài tập Hình học Khối đa diện có lời giải chi tiết

Trắc Nghiệm Tổng Hợp Toán 12 (Có Đáp Án)
Lớp 12;Toán

Thời gian làm bài: 1 giờ

Chọn mã đề:

Bạn chưa làm Đề số 1!!!

Hãy bắt đầu chinh phục nào!

Xem trước nội dung:

Câu 1: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB = $a \sqrt{3}$ , AC = $2 a$ . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng ( ABC) . Tính theo a thể tích khối chóp S.ABC ta được kết quả:

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3}}{2}

\frac{a^{3} \sqrt{3}}{2}

\frac{3 a^{3}}{4}

Câu 2: 1 điểm

Tính thể tích V của khối lăng trụ tam giác có chiều cao bằng 6 và diện tích đáy bằng 10

V = 10

V = 30

V = 20

V = 60

Câu 3: 1 điểm

Cho hình chóp tứ giác đều có cạnh đáy bằng a và độ dài đường cao bằng $\frac{a \sqrt{14}}{2}$ .Tính tang của góc giữa cạnh bên và mặt đáy

\sqrt{7}

\frac{\sqrt{14}}{2}

\sqrt{14}

\frac{7}{2}

Câu 4: 1 điểm

Cho hình chóp tứ giác đều $S . A B C D$ đỉnh S , khoảng cách từ C đến mặt phẳng (SAB) bằng 6 . Gọi V là thể tích khối chóp $S . A B C D$ , tính giá trị nhỏ nhất của V .

18 \sqrt{3}

64 \sqrt{3}

27 \sqrt{3}

54 \sqrt{3}

Câu 5: 1 điểm

Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh 2a và $\hat{S B A} = \hat{S C A} = 90^{o}$ Biết góc giữa đường thẳng SA và mặt đáy bằng $45^{o}$ . Tính khoảng cách từ điểm B đến mặt phẳng (SAC).

\frac{\sqrt{15}}{5} a

\frac{2 \sqrt{15}}{5} a

\frac{2 \sqrt{15}}{3} a

\frac{2 \sqrt{51}}{5} a

Câu 6: 1 điểm

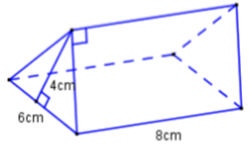
Cho khối đa diện (kích thước như hình vẽ bên) được tạo bởi ba hình chữ nhật và hai tam giác bằng nhau. Tính thể tích khối đa diện đã cho

48 c m^{3}

192 c m^{3}

32 c m^{3}

96 c m^{3}

Câu 7: 1 điểm

Cho hình chóp đều S.ABCD có $S A = a \sqrt{5}$ , AB = $a$ . Gọi M, N, P, Q lần lượt là trung điểm của SA, SB,SC,SD . Tính cosin của góc giữa hai đường thẳng DN và mặt phẳng (MQP) ?

\frac{\sqrt{2}}{2}

\frac{1}{2}

\frac{\sqrt{3}}{2}

\frac{\sqrt{15}}{6}

Câu 8: 1 điểm

Cho hình chóp S.ABC có cạnh $S A ⊥ (A B C)$ , tam giác ABC đều và $A B = a$ ; góc giữa SB và mặt phẳng (ABC) bằng $60^{o}$ . Gọi M,N lần lượt là trung điểm của SA,SB. Tính thể tích khối chóp $S . M N C$ :

\frac{a^{3}}{16}

\frac{a^{3}}{4}

\frac{a^{3} \sqrt{3}}{12}

\frac{a^{3}}{8}

Câu 9: 1 điểm

Cho hình chóp $S . A B C D$ có đáy ABCD là hình vuông tâm O cạnh 2a . Hình chiếu của S trên mặt đáy là trung điểm H của OA ; góc giữa hai mặt phẳng (SCD) và ( ABCD) bằng 45⁰ . Tính khoảng cách giữa hai đường thẳng AB và SC

a \sqrt{2}

\frac{3 a \sqrt{2}}{2}

\frac{3 a \sqrt{2}}{4}

a \sqrt{6}

Câu 10: 1 điểm

Cho hình hộp chữ nhật ABCD.A'B'C'D' có $A B = B C = a;$ $A' A = a \sqrt{3}$ . Gọi I là giao điểm của AD' và A’D ; H là hình chiếu của I trên mặt phẳng $(A' B' C' D')$ , K là hình chiếu của B lên mặt phẳng $(C A' B')$ . Tính thể tích khối tứ diện IHBK ?

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{16}

\frac{a^{3} \sqrt{3}}{8}

Câu 11: 1 điểm

Thể tích của khối lập phương có cạnh bằng 2 là

\frac{8}{3}

Câu 12: 1 điểm

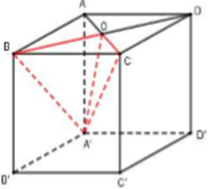
Cho hình lập phương ABCD.A’B’C’D; cạnh bằng a. Gọi O là giao điểm của AC và BD. Thể tích của tứ diện OA’BC bằng

\frac{a^{3}}{12}

\frac{a^{3}}{24}

\frac{a^{3}}{6}

\frac{a^{3}}{4}

Câu 13: 1 điểm

Thể tích V của khối hộp chữ nhật ABCD.A’B’C’D’ biết $A B = a; A D = 2 a$ ; $A C' = a \sqrt{14}$ là

V = 6 a^{3}

V = \frac{a^{3} \sqrt{14}}{3}

V = a^{3} \sqrt{5}

V = 2 a^{3}

Câu 14: 1 điểm

Cho lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Thể tích của khối cầu đi qua các đỉnh của lăng trụ bằng

\frac{1}{18 \sqrt{3}} \sqrt{{(4 a^{2} + b^{2})}^{3}}

\frac{π}{18 \sqrt{3}} \sqrt{{(4 a^{2} + 3 b^{2})}^{3}}

\frac{π}{18 \sqrt{3}} \sqrt{{(4 a^{2} + b^{2})}^{3}}

\frac{π}{18 \sqrt{2}} \sqrt{{(4 a^{2} + 3 b^{2})}^{3}}

Câu 15: 1 điểm

Cho tứ diện ABCD có $A B = a$ ; $A C = a \sqrt{2}$ ; $A D = a \sqrt{3}$ các tam giác ABC, ACD, ABD là các tam giác vuông tại đỉnh A. Khoảng cách d từ điểm A đến mặt phẳng (BCD) là

d = \frac{a \sqrt{66}}{11}

d = \frac{a \sqrt{6}}{3}

d = \frac{a \sqrt{30}}{5}

d = \frac{a \sqrt{3}}{2}

Câu 16: 1 điểm

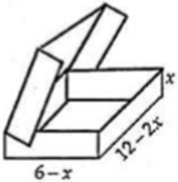
Một hộp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên hộp được rải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi $x = x_{o}$ là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị V₀ bằng

V_{o} = 64 (d v t t)

V_{o} = \frac{64}{3} (d v t t)

V_{o} = 16 (d v t t)

V_{o} = 48 (d v t t)

Câu 17: 1 điểm

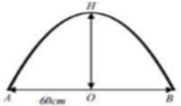
Bạn An cần mua một chiếc gương đường viền là Parabol bậc 2 (xem hình vẽ). Biết rằng khoảng cách đoạn AB = 60cm, OH = 30cm. Diện tích của chiếc gương bạn An mua là:

400

650

1200

2100

Câu 18: 1 điểm

Cho hình chóp S.ABCD có SA vuông góc với đáy; $S A = a \sqrt{6}$ . Đáy ABCD là hình thang vuông tại A và B, $A B = B C = \frac{1}{2} A D = a$ . Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ECD.

R = \frac{a \sqrt{30}}{3}

R = a \sqrt{\frac{19}{6}}

R = a \sqrt{6}

R = a \sqrt{\frac{114}{6}}

Câu 19: 1 điểm

Tính thể tích V của khối chóp có đáy là hình vuông cạnh 3 và chiều cao bằng 4.

V = 16

V = 48

V = 12

V = 36

Câu 20: 1 điểm

Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A với BC = a và mặt bên AA’B’B là hình vuông. Thể tích khối lăng trụ ABC.A’B’C’ bằng

\frac{\sqrt{2}}{8} a^{3}

\frac{\sqrt{2}}{4} a^{3}

\frac{1}{4} a^{3}

\frac{1}{12} a^{3}

Xem thêm đề thi tương tự

Bài tập Hình học Khối đa diện cơ bản, nâng cao có lời giải chi tiếtLớp 12Toán

Trắc Nghiệm Tổng Hợp Toán 12 (Có Đáp Án)
Lớp 12;Toán

118 câu hỏi 4 mã đề 1 giờ

185,546 lượt xem 99,897 lượt làm bài