Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải

Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a. Mặt phẳng (AB'C') tạo với mặt đáy góc 60º . Tính theo a thể tích khối lăng trụ ABC.A'B'C'.

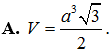
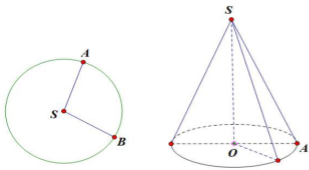
Cho hình nón đỉnh S, đáy là đường tròn (O; 5). Một mặt phẳng đi qua đỉnh của hình nón cắt đường tròn đáy tại hai điểm A và B sao cho SA = AB = 8. Tính khoảng cách từ O đến (SAB).

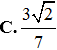
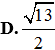
Một hình trụ có hai đường tròn đáy nằm trên một mặt cầu bán kính R và có đường cao bằng bán kính mặt cầu. Diện tích toàn phần hình trụ đó bằng

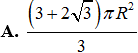
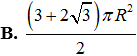
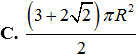
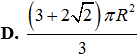
Cho hình tròn tâm S, bán kính R = 2 . Cắt đi $\frac{1}{4}$ hình tròn rồi dán lại để tạo ra mặt xung quanh của hình nón như hình vẽ. Tính diện tích toàn phần của hình nón đó.

Cho lăng trụ tam giác đều ABC.A’B’C’ có độ dài cạnh đáy bằng 3a và chiều cao bằng 8a. Tính bán kính R của mặt cầu ngoại tiếp tứ diện AB’C’C.

Khi cắt mặt cầu S (O, R) bởi một mặt kính đi qua tâm O, ta được hai nửa mặt cầu giống nhau. Giao tuyến của mặt kính đó với mặt cầu gọi là mặt đáy của mỗi nửa mặt cầu. Một hình trụ gọi là nội tiếp nửa mặt cầu S (O, R) nếu một đáy của hình trụ nằm trong đáy của nửa mặt cầu, còn đường tròn đáy kia là giao tuyến của hình trụ với nửa mặt cầu. Biết R = 1, tính bán kính đáy r và chiều cao h của hình trụ nội tiếp nửa mặt cầu S (O, R) để khối trụ có thể tích lớn nhất.

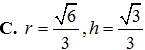
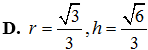
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, cạnh AC=b, góc ACB= $60°$. Góc giữa đường thẳng BC' và mặt phẳng (AA'C'C) bằng 30 $°$. Tính theo b diện tích xung quanh của hình lăng trụ ABC.A'B'C'.

Một hình nón có góc ở đỉnh bằng 60 $°$, đường sinh bằng 2a. Diện tích xung quanh của hình nón là

Cắt một hình trụ bằng mặt phẳng $\left(\alpha \right)$ vuông góc mặt đáy, ta được thiết diện là một hình vuông có diện tích bằng 16. Biết khoảng cách từ tâm đáy hình trụ đến mặt phẳng $\left(\alpha \right)$ bằng 3. Tính thể tích khối trụ

Cho $\frac{x-1}{1}=\frac{y+2}{1}=\frac{z}{1}$ và (P): 2x+y-2z+2=0, mặt cầu (S) có tâm nằm trên đường thẳng (d), tiếp xúc với (P) và đi qua A(2;-1;0) có tọa độ tâm I là

Cho hình nón tròn xoay có chiều cao h=20(cm), bán kính đáy r=25(cm). Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12(cm). Tính diện tích của thiết diện đó.

Cho tam giác OAB vuông cân tại O có AB = 2. Gọi H là trung điểm của AB. Tính diện tích xung quanh S_xq của hình nón sinh bởi khi tam giác OAB quay quanh OH.

Cho khối trụ có bán kính đáy R và có chiều cao h = 2R . Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O’. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O’) ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?

Một hình trụ có chu vi của đường tròn đáy là c, chiều cao của hình trụ gấp 4 lần chu vi đáy. Thể tích của khối trụ này là

Cho hình lăng trụ ABC $A_1{B}_1{C}_1$ có diện

tích mặt bên AB $B_1{A}_1$ bằng 4. Khoảng

cách giữa cạnh C $C_1$ và mặt phẳng

(AB $B_1{A}_1$) bằng 7. Tính thể tích khối

lăng trụ ABC $A_1{B}_1{C}_1$.

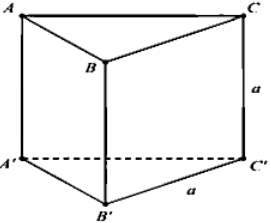
Cho lăng trụ đều ABC.A'B'C' có tất cả các cạnh đều bằng a (hình vẽ bên dưới). Khoảng cách giữa hai đường thẳng AC và bằng?

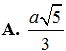
Cắt hình nón bởi một mặt phẳng đi qua trục ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng $a\sqrt{6}$. Tính thể tích V của khối nón đó.

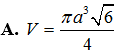
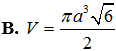
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng $8\mathrm{\pi }$(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S)  (D không thuộc đường tròn (C)) và tam giác ABC đều. Tính thể tích lớn nhất của tứ diện ABCD.

Cho hàm số f(x) có đạo hàm liên tục trên R và có f(1)=1; f(-1)= $-\frac{1}{3}$. Đặt g(x)= ${\left(f\left(x\right)\right)}^2-4f\left(x\right)$. Cho biết đồ thị của y=f'(x) có dạng như hình vẽ dưới đây

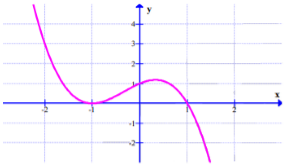
Mệnh đề nào sau đây đúng?

Cho hình trụ có diện tích xung quanh bằng $4\mathrm{\pi }$, thiết diện qua trục là hình vuông. Thể tích của khối trụ giới hạn bởi hình trụ bằng

Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Diện tích xung quanh của khối nón có đỉnh là tâm hình vuông A’B’C’D’ và có đường tròn đáy ngoại tiếp hình vuông ABCD bằng

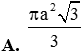
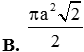
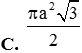
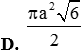
Cho tứ diện ABCD có (ABC) vuông góc với (DBC), hai tam giác ABC, DBC là các tam giác đều cạnh a. Gọi (S) là mặt cầu đi qua B, C và tiêp xúc với đường thẳng AD tại A. Bán kính R của mặt cầu (S) bằng

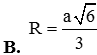
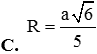
Cho hình nón có độ dài đường sinh bằng 4, góc giữa đường sinh và mặt đáy bằng $30°$. Diện tích toàn phần của hình nón đã cho bằng

Cho hình lăng trụ đều ABCA'B'C' có tất cả các cạnh bằng a. Diện tích xung quanh của mặt cầu ngoại tiếp hình lăng trụ bằng 

Cho  hình chóp SABC có đáy là tam giác vuông tại B, AC=2a, SA vuông góc với đáy, SA=a. Bán kính r của mặt cầu ngoại tiếp hình chóp SABC bằng

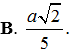
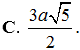
Cho hình cầu đường kính AA'=2a. Gọi H là điểm nằm trên đoạn AA’ sao cho AH= $\frac{4a}{3}$. Mặt phẳng (P) đi qua H và vuông góc với AA’ cắt hình cầu theo đường tròn (C). Diện tích của hình tròn (C) bằng

Trong không gian, cho tam giác ABC vuông tại A, AB=a, ABC=60 $°$. Quay tam giác đó một vòng xung quanh BC, ta được một hình tròn xoay. Diện tích xung quanh của hình tròn xoay đó bằng

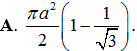
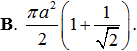
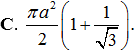
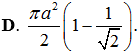
Cho hình trụ có hai đáy là hai hình tròn tâm O và O', bán kính đáy bằng r và một hình nón có đỉnh là O đáy là hình tròn tâm O'. Biết diện tích xung quanh của hình nón bằng hai lần diện tích đáy của nó. Tính thể tích V của khối trụ giới hạn bởi hình trụ đã cho.

Cho mặt cầu có bán kính R và cho một hình trụ có bán kính đáy R, chiều cao 2R. Tỉ số diện tích mặt cầu và diện tích xung quanh của hình trụ là

Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng  một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của khối nón đỉnh S đáy là hình tròn tâm O' bằng bao nhiêu, biết rằng thể tích của nó bằng $\frac{1}{8}$ thể tích khối nón đỉnh S, đáy là hình tròn tâm O.

Cho khối trụ $\left(\mu \right)$ có bán kính đáy bằng 5 và có diện tích xung quanh bằng 30 $\mathrm{\pi }$. Tính thể tích V của khối trụ  $\left(\mu \right)$.

Một hình trụ có hai đáy là hai hình tròn tâm O và O’, bán kính đáy R, chiều cao $R\sqrt{2}$. Mặt phẳng (P) đi qua OO' cắt hình trụ theo một thiết diện có diện tích bằng bao nhiêu?

Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=2, các cạnh bên đều bằng 2. Tính thể tích của khối cầu ngoại tiếp hình chóp SABC bằng

Cho khối trụ có bán kính đáy R = 5cm. Khoảng cách 2 đáy h = 7cm . Cắt khối trụ bằng 1 mặt phẳng song song với trục và cách trục 3cm. Diện tích của thiết diện bằng

Cho hình hộp ABCD.A'B'C'D' có AB = AD = 2a, AA' = 4a . Lấy M, N, P, Q lần lượt là trung điểm của AA’, BB’, CC’, DD’. Biết hình hộp chữ nhật ABCD.A'B'C'D' nội tiếp khối trụ (T) và lăng trụ ABCD.MNPQ nội tiếp mặt cầu (C). Tỉ số thể tích $\frac{V_{\left(T\right)}}{V_{\left(C\right)}}$ giữa khối cầu và khối trụ là.

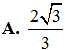
Cắt một khối trụ bởi một mặt phẳng vuông góc với trục của nó ta được thiết diện là một hình tròn có chu vi bằng chu vi vủa hình chữ nhật được tạo thành khi cắt mặt trụ bởi 1 mặt phẳng đi qua 2 tâm. Khi đó tỉ số $\frac{S_{xq}}{S_{tp}}$ của khối trụ bằng:

Cho lăng trụ tứ giác đều ABCD.A'B'C'D' có cạnh đáy bằng 2a. Khoảng cách từ A đến mặt phẳng (A'BC) bằng $a\sqrt{3}$. Thể tích khối lăng trụ là.

Cho hình nón có độ dài đường cao là $a\sqrt{3}$, bán kính đáy là a. Số đo của góc ở đỉnh là.

Cho mặt cầu $\left(S\right):{\left(x-2\right)}^2+y^2+{\left(z+1\right)}^2=14$. Mặt cầu (S) cắt trục Oy tại A, B $\left(y_A<y_B\right)$. Mặt phẳng tiếp xúc với mặt cầu (S) tại B là.

Cho hình nón có đường cao h = 3 và bán kính đáy R = 4. Diện tích xung quanh $S_{xq}$ của hình nón là