Trang chủ Đề thi THPT Quốc gia Toán Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 91
thumbnail

Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 91

Đề thi thử THPT Quốc gia môn Toán năm 2021, được thiết kế bám sát cấu trúc của Bộ Giáo dục. Các câu hỏi trọng tâm như logarit, tích phân, hình học không gian, và bài toán thực tế giúp học sinh ôn tập toàn diện và chuẩn bị tốt nhất cho kỳ thi. Đề thi có đáp án chi tiết, hỗ trợ học sinh tự đánh giá năng lực và cải thiện điểm số hiệu quả.

Từ khoá: Toán học logarit tích phân hình học không gian bài toán thực tế năm 2021 đề thi thử đề thi có đáp án ôn thi lớp 12

Thời gian làm bài: 1 giờ

Đề thi nằm trong bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết


Bạn chưa làm đề thi này!!!

Hãy bắt đầu chinh phục nào!



 

Xem trước nội dung:

Câu 1: 0.2 điểm

Trong không gian tọa độ Oxyz, đường thẳng (d):x+52=y−7−8=z+139\left( d \right):\frac{x+5}{2}=\frac{y-7}{-8}=\frac{z+13}{9} có một véc tơ chỉ phương là

A.  
u1→=(2; −8; 9).\overrightarrow {{u_1}} = \left( {2;\, - 8;\,9} \right).
B.  
u2→=(2; 8; 9).\overrightarrow {{u_2}} = \left( {2;\,8;\,9} \right).
C.  
u3→=(−5; 7; −13).\overrightarrow {{u_3}} = \left( { - 5;\,7;\, - 13} \right).
D.  
u4→=(5; −7; −13).\overrightarrow {{u_4}} = \left( {5;\, - 7;\, - 13} \right).
Câu 2: 0.2 điểm

Hình vẽ bên là đồ thị của hàm số nào?

Hình ảnh

A.  
y=x3−4xy = {x^3} - 4x
B.  
y=x4−4x2y = {x^4} - 4{x^2}
C.  
y=−x4+4x2y = - {x^4} + 4{x^2}
D.  
y=−x3+4xy = - {x^3} + 4x
Câu 3: 0.2 điểm

Trong không gian Oxyz, mặt phẳng (α):x−y+2z−3=0\left( \alpha \right):x-y+2z-3=0 đi qua điểm nào dưới đây?

A.  
M(1 ; 1; 32)M\left( {1\,;\,1;\,\frac{3}{2}} \right)
B.  
N(1 ;−1 ;−32)N\left( {1\,; - 1\,; - \frac{3}{2}} \right)
C.  
P(1 ; 6 ; 1)P\left( {1\,;\,6\,;\,1} \right)
D.  
Q(0 ; 3 ; 0)Q\left( {0\,;\,3\,;\,0} \right)
Câu 4: 0.2 điểm

Với α\alpha là một số thực bất kỳ, mệnh đề nào sau đây sai?

A.  
(10α)2=10α2{\left( {{{10}^\alpha }} \right)^2} = {10^{{\alpha ^2}}}
B.  
(10α)2=(100)α{\left( {{{10}^\alpha }} \right)^2} = {\left( {100} \right)^\alpha }
C.  
10α=(10)α\sqrt {{{10}^\alpha }} = {\left( {\sqrt {10} } \right)^\alpha }
D.  
10α=10α2\sqrt {{{10}^\alpha }} = {10^{\frac{\alpha }{2}}}
Câu 5: 0.2 điểm

Tính diện tích xung quanh S\) của khối trụ có bán kính đáy \(r=4\) và chiều cao \(h=3.

A.  
S=96πS = 96\pi
B.  
S=12πS = 12\pi
C.  
S=48πS = 48\pi
D.  
S=24πS = 24\pi
Câu 6: 0.2 điểm

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x+4y-4z-25=0\). Tìm tọa độ tâm I và bán kính R của mặt cầu \(\left( S \right).

A.  
I(−1 ; −2 ; 2);R=6I\left( -1\,;\,-2\,;\,2 \right); R=6.
B.  
I(1 ; −2 ; 2);R=34I\left( 1\,;\,-2\,;\,2 \right); R=\sqrt{34}
C.  
I(−1 ; 2 ; −2);R=5I\left( -1\,;\,2\,;\,-2 \right); R=5
D.  
I(−2;4;−4);R=29I\left( -2;4;-4 \right); R=\sqrt{29}
Câu 7: 0.2 điểm

Trong không gian Oxyz, hình chiếu vuông góc của điểm A\left( 3\,;\,2\,;\,-4 \right)\) lên mặt phẳng \(\left( Oxy \right) có tọa độ là

A.  
(3 ; 0 −4)\left( {3\,;\,0\, - 4} \right)
B.  
(0 ; 0 −4)\left( {0\,;\,0\, - 4} \right)
C.  
(0 ; 2 −4)\left( {0\,;\,2\, - 4} \right)
D.  
(3 ; 2 ; 0)\left( {3\,;\,2\,;\,0} \right)
Câu 8: 0.2 điểm

Cho dãy số 12;0;−12;−1;−32;.....\frac{1}{2};0;-\frac{1}{2};-1;-\frac{3}{2};..... là cấp số cộng với

A.  
Số hạng đầu tiên là 0, công sai là −12.-\frac{1}{2}.
B.  
Số hạng đầu tiên là
C.  
Số hạng đầu tiên là
D.  
Số hạng đầu tiên là 0, công sai là 12.\frac{1}{2}.
Câu 9: 0.2 điểm

Đạo hàm của hàm số y=πxy={{\pi }^{x}} là

A.  
y′=πxln⁡πy' = \frac{{{\pi ^x}}}{{\ln \pi }}
B.  
y′=πx.ln⁡πy' = {\pi ^x}.\ln \pi
C.  
y′=x.πx−1y' = x.{\pi ^{x - 1}}
D.  
y′=xπx−1ln⁡πy' = x{\pi ^{x - 1}}\ln \pi
Câu 10: 0.2 điểm

Cho tập hợp A gồm có 9 phần tử. Số tập con gồm có 4 phần tử của tập hợp A là

A.  
4.9
B.  
A94A_9^4
C.  
P4
D.  
C94C_9^4
Câu 11: 0.2 điểm

Cho hàm số y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu \({f}'\left( x \right) như sau

Hình ảnh

Mệnh đề nào sau đây sai?

A.  
Hàm số y=f(x)y=f\left( x \right) có hai điểm cực trị
B.  
Hàm số y=f(x)y=f\left( x \right) đạt cực đại tại x=1.
C.  
Hàm số y=f(x)y=f\left( x \right) đạt cực tiểu tại x=-1.
D.  
Hàm số y=f(x)y=f\left( x \right) đạt cực trị tại x=-2.
Câu 12: 0.2 điểm

Cho đồ thị hàm số y=f(x)y=f\left( x \right) có đồ thị như hình vẽ bên dưới

Hình ảnh

Hàm số y=f(x)y=f\left( x \right) đồng biến trên khoảng nào dưới đây?

A.  
(2;  +∞)\left( 2;\,\,+\infty \right).
B.  
(0;2)\left( 0;2 \right).
C.  
(− ∞;  0)\left( { - \,\infty ;\,\,0} \right)
D.  
(−2;  2)\left( { - 2;\,\,2} \right)
Câu 13: 0.2 điểm

Cho hàm f\left( x \right)\) có đạo hàm liên tục trên \(\left[ 2;3 \right]\) đồng thời \(f\left( 2 \right)=2,f\left( 3 \right)=5\). Khi đó \(\int\limits_{2}^{3}{{f}'\left( x \right)}\text{d}x bằng

A.  
3
B.  
10
C.  
-3
D.  
7
Câu 14: 0.2 điểm

Cho số phức z=−1+2i , w=2−iz=-1+2i\,,\,w=2-i. Điểm nào trong hình bên biểu diễn số phức z+w?

Hình ảnh

A.  
P
B.  
Q
C.  
M
D.  
N
Câu 15: 0.2 điểm

Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a, SB=b, SC=c. Tính thể tích V của khối chóp đó theo a, b, c.

A.  
V = abc
B.  
V=abc6V = \frac{{abc}}{6}
C.  
V=abc3V = \frac{{abc}}{3}
D.  
V=abc2V = \frac{{abc}}{2}
Câu 16: 0.2 điểm

Cho số phức {{z}_{1}}=1+i\) và \({{z}_{2}}=2-3i\). Tìm số phức liên hợp của số phức \(\text{w}={{z}_{1}}+{{z}_{2}}?

A.  
w‾=3+2i\overline {\rm{w}} = 3 + 2i
B.  
w‾=1−4i\overline {\rm{w}} = 1 - 4i
C.  
w‾=−1+4i\overline {\rm{w}} = - 1 + 4i
D.  
w‾=3−2i\overline {\rm{w}} = 3 - 2i
Câu 17: 0.2 điểm

Cho hàm số f\left( x \right)={{2}^{x}}+x+1\). Tìm \(\int{f\left( x \right)\text{d}x}

A.  
∫f(x)dx=2x+x2+x+C\int {f\left( x \right){\rm{d}}x} = {2^x} + {x^2} + x + C
B.  
∫f(x)dx=1ln⁡22x+12x2+x+C\int {f\left( x \right){\rm{d}}x} = \frac{1}{{\ln 2}}{2^x} + \frac{1}{2}{x^2} + x + C
C.  
∫f(x)dx=2x+12x2+x+C\int {f\left( x \right){\rm{d}}x} = {2^x} + \frac{1}{2}{x^2} + x + C
D.  
∫f(x)dx=1x+12x+12x2+x+C\int {f\left( x \right){\rm{d}}x} = \frac{1}{{x + 1}}{2^x} + \frac{1}{2}{x^2} + x + C
Câu 18: 0.2 điểm

Đường tiệm cận ngang, đường tiệm cận đứng của đồ thị hàm số y=2x−1x−2y=\frac{2x-1}{x-2} lần lượt có phương trình là

A.  
y = 2,x = 2
B.  
y=2, x=12y = 2,\,x = \frac{1}{2}
C.  
x = 2,y = 2
D.  
y = 2,x = - 2
Câu 19: 0.2 điểm

Nghiệm của bất phương trình 3x+2≥19{{3}^{x+2}}\ge \frac{1}{9} là

A.  
x < 0
B.  
x≥−4x \ge - 4
C.  
x≥0x \ge 0
D.  
x < 4
Câu 20: 0.2 điểm

Cho hình nón có bán kính đáy r=\sqrt{3}\) và độ dài đường sinh l=4. Tính diện tích xung quanh \({{S}_{xq}} của hình nón đã cho.

A.  
Sxq=12π{S_{xq}} = 12\pi
B.  
Sxq=43π{S_{xq}} = 4\sqrt 3 \pi
C.  
Sxq=39π{S_{xq}} = \sqrt {39} \pi
D.  
Sxq=83π{S_{xq}} = 8\sqrt 3 \pi
Câu 21: 0.2 điểm

Cho tứ diện ABCD có AC=AD và BC=BD. Gọi I là trung điểm của CD. Khẳng định nào sau đây sai?

A.  
Góc giữa 2 mặt phẳng .
B.  
(BCD)⊥(AIB)\left( BCD \right)\bot \left( AIB \right).
C.  
Góc giữa 2 mặt phẳng .
D.  
(ACD)⊥(AIB)\left( ACD \right)\bot \left( AIB \right)
Câu 22: 0.2 điểm

Biết rằng có duy nhất một cặp số thực \left( x;\ y \right)\) thỏa mãn \(\left( x+y \right)+\left( x-y \right)i=5+3i. Tính S=x+2y.

A.  
S = 5
B.  
S = 3
C.  
S = 4
D.  
S = 6
Câu 23: 0.2 điểm

Giá trị lớn nhất của hàm số f\left( x \right)=\frac{{{x}^{2}}-8x}{x+1}\) trên đoạn \(\left[ 1;3 \right] bằng

A.  
-3
B.  
-4
C.  
−154 - \frac{{15}}{4}
D.  
−72 - \frac{7}{2}
Câu 24: 0.2 điểm

Số nghiệm của phương trình log⁡2(x2 −  x + 2)=1{{\log }_{2}}\left( {{x}^{2}}\,-\,\,x\,+\,2 \right)=1 là

A.  
0
B.  
3
C.  
1
D.  
2
Câu 25: 0.2 điểm

Nguyên hàm của hàm số f(x)=3x+2f\left( x \right)=\sqrt{3x+2} là

A.  
3213x+2+C\frac{3}{2}\frac{1}{{\sqrt {3x + 2} }} + C
B.  
23(3x+2)3x+2+C\frac{2}{3}(3x + 2)\sqrt {3x + 2} + C
C.  
13(3x+2)3x+2+C\frac{1}{3}(3x + 2)\sqrt {3x + 2} + C
D.  
29(3x+2)3x+2+C\frac{2}{9}(3x + 2)\sqrt {3x + 2} + C
Câu 26: 0.2 điểm

Trong không gian với hệ tọa độ Oxyz, đường thẳng \Delta \) đi qua điểm \(A\left( -2\,;\,4\,;\,3 \right)\) và vuông góc với mặt phẳng \(\left( \alpha \right):\,2x-3y+6z+19=0 có phương trình là

A.  
x−2−2=y+34=z−63\frac{{x - 2}}{{ - 2}} = \frac{{y + 3}}{4} = \frac{{z - 6}}{3}
B.  
x+22=y−4−3=z−36\frac{{x + 2}}{2} = \frac{{y - 4}}{{ - 3}} = \frac{{z - 3}}{6}
C.  
x+2−2=y−34=z+63\frac{{x + 2}}{{ - 2}} = \frac{{y - 3}}{4} = \frac{{z + 6}}{3}
D.  
x−22=y+4−3=z+36\frac{{x - 2}}{2} = \frac{{y + 4}}{{ - 3}} = \frac{{z + 3}}{6}
Câu 27: 0.2 điểm

Cho hàm số f\left( x \right)\) có đạo hàm \({f}'\left( x \right)={{x}^{3}}\left( x-1 \right)\left( x-2 \right),\,\forall x\in \mathbb{R}. Số điểm cực trị của hàm số đã cho là

A.  
5
B.  
2
C.  
1
D.  
3
Câu 28: 0.2 điểm

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD),SAB^=300,SA=2a\left( ABCD \right), \widehat{SAB}={{30}^{0}}, SA=2a. Tính thể tích V của khối chóp S.ABCD.

A.  
V=a39.V = \frac{{{a^3}}}{9}.
B.  
V=a33.V = \frac{{{a^3}}}{3}.
C.  
V=3a36.V = \frac{{\sqrt 3 {a^3}}}{6}.
D.  
V=a3.V = {a^3}.
Câu 29: 0.2 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA\bot \left( ABCD \right)\). Gọi I là trung điểm của SC. Khoảng cách từ $I$ đến mặt phẳng \(\left( ABCD \right) bằng độ dài đoạn thẳng nào?

A.  
IB
B.  
IC
C.  
IA
D.  
IO
Câu 30: 0.2 điểm

Với hai số thực dương a,\,b\) thỏa mãn \(\frac{{{\log }_{3}}5{{\log }_{5}}a}{1+{{\log }_{3}}2}-{{\log }_{6}}b=2. Khẳng định nào dưới đây là khẳng định đúng?

A.  
a=blog⁡63a = b{\log _6}3
B.  
a=blog⁡62a = b{\log _6}2
C.  
a = 36b
D.  
2a + 3b = 0
Câu 31: 0.2 điểm

Bất phương trình {{4}^{x-15}}<32 có bao nhiêu nghiệm nguyên dương?

A.  
22
B.  
18
C.  
17
D.  
23
Câu 32: 0.2 điểm

Giá trị của tích phân I=∫01xx+1dxI=\int\limits_{0}^{1}{\frac{x}{x+1}}\text{d}x là

A.  
I=1+ln⁡2I = 1 + \ln 2
B.  
I=2−ln⁡2I = 2 - \ln 2
C.  
I=1−ln⁡2I = 1 - \ln 2
D.  
I=2+ln⁡2I = 2 + \ln 2
Câu 33: 0.2 điểm

Hàm số y=2018x−x2y=\sqrt{2018x-{{x}^{2}}} nghịch biến trên khoảng nào trong các khoảng sau đây?

A.  
(1;2018)
B.  
(1010;2018)
C.  
(2018;+∞)\left( {2018; + \infty } \right)
D.  
(0;1009)
Câu 34: 0.2 điểm

Tìm số phức z thỏa mãn (2−3i)z−(9−2i)=(1+i)z.\left( 2-3i \right)z-\left( 9-2i \right)=\left( 1+i \right)z.

A.  
1 + 2i
B.  
1 - 2i
C.  
135+165i\frac{{13}}{5} + \frac{{16}}{5}i
D.  
- 1 - 2i
Câu 35: 0.2 điểm

Tổ 1 lớp 11A có 6 nam và 7 nữ; tổ 2 có 5 nam và 8 nữ. Chọn ngẫu nhiên mỗi tổ một học sinh. Xác suất để 2 học sinh được chọn đều là nữ là

A.  
2839\frac{{28}}{{39}}
B.  
15169\frac{{15}}{{169}}
C.  
56169\frac{{56}}{{169}}
D.  
30169\frac{{30}}{{169}}
Câu 36: 0.2 điểm

Trong hình vẽ bên, điểm A biểu diễn số phức {{z}_{1}}\), điểm B biểu diễn số phức \({{z}_{2}}\) sao cho điểm B đối xứng với điểm A qua gốc tọa độ O. Tìm \(\left| z \right|\) biết số phức \(z={{z}_{1}}+3{{z}_{2}}.

Hình ảnh

A.  
17\sqrt {17}
B.  
4
C.  
252\sqrt 5
D.  
5
Câu 37: 0.2 điểm

Một đường thẳng cắt đồ thị hàm số y={{x}^{4}}-2{{x}^{2}}\) tại 4 điểm phân biệt có hoành độ là 0, 1, m và n. Tính \(S={{m}^{2}}+{{n}^{2}}.

A.  
S = 1
B.  
S = 2
C.  
S = 3
D.  
S = 0
Câu 38: 0.2 điểm

Trong không gian Oxyz, cho hai điểm A(2 ; 3 ; −5),B(−4 ; 1 ; 3)A\left( 2\,;\,3\,;\,-5 \right), B\left( -4\,;\,1\,;\,3 \right). Viết phương trình mặt cầu đường kính AB.

A.  
(x − 1)2 + (y − 2)2 + (z − 1)2 = 26{\left( {x\, - \,1} \right)^2}\, + \,{\left( {y\, - \,2} \right)^2}\, + \,{\left( {z\, - \,1} \right)^2}\, = \,26
B.  
(x − 1)2 + (y + 2)2 + (z − 1)2 = 26{\left( {x\, - \,1} \right)^2}\, + \,{\left( {y\, + \,2} \right)^2}\, + \,{\left( {z\, - \,1} \right)^2}\, = \,26
C.  
(x + 1)2 + (y + 2)2 + (z + 1)2 = 26{\left( {x\, + \,1} \right)^2}\, + \,{\left( {y\, + \,2} \right)^2}\, + \,{\left( {z\, + \,1} \right)^2}\, = \,26
D.  
(x + 1)2 + (y − 2)2 + (z + 1)2 = 26{\left( {x\, + \,1} \right)^2}\, + \,{\left( {y\, - \,2} \right)^2}\, + \,{\left( {z\, + \,1} \right)^2}\, = \,26
Câu 39: 0.2 điểm

Cho hình phẳng giới hạn bởi đồ thị hàm số y=f\left( x \right)\) và trục hoành gồm 2 phần, phần nằm phía trên trục hoành có diện tích \({{S}_{1}}=\frac{8}{3}\) và phần nằm phía dưới trục hoành có diện tích \({{S}_{2}}=\frac{5}{12}\). Tính \(I=\int\limits_{-1}^{0}{f\left( 3x+1 \right)\text{d}x}.

Hình ảnh

A.  
I=274I = \frac{{27}}{4}
B.  
I=53I = \frac{5}{3}
C.  
I=34I = \frac{3}{4}
D.  
I=3736I = \frac{{37}}{{36}}
Câu 40: 0.2 điểm

Trong không gian Oxyz, cho điểm M(1;\,0;\,1)\) và đường thẳng \(d:\frac{x-1}{1}=\frac{y-2}{2}=\frac{z-3}{3}. Đường thẳng đi qua M, vuông góc với d và cắt Oz có phương trình là

A.  
{x=1−3ty=0z=1+t\left\{ \begin{array}{l} x = 1 - 3t\\ y = 0\\ z = 1 + t \end{array} \right.
B.  
{x=1−3ty=0z=1−t\left\{ \begin{array}{l} x = 1 - 3t\\ y = 0\\ z = 1 - t \end{array} \right.
C.  
{x=1−3ty=tz=1+t\left\{ \begin{array}{l} x = 1 - 3t\\ y = t\\ z = 1 + t \end{array} \right.
D.  
{x=1+3ty=0z=1+t\left\{ \begin{array}{l} x = 1 + 3t\\ y = 0\\ z = 1 + t \end{array} \right.
Câu 41: 0.2 điểm

Cho hàm số y=f(x) có đạo hàm tại \forall x\in \mathbb{R}\), hàm số \({f}'(x)={{x}^{3}}+a{{x}^{2}}+bx+c

Có đồ thị

Hình ảnh

Số điểm cực trị của hàm số y=f[f′(x)]y=f\left[ {f}'\left( x \right) \right] là

A.  
7
B.  
11
C.  
9
D.  
8
Câu 42: 0.2 điểm

S là tập tất cả các số nguyên dương của tham số m sao cho bất phương trình {{4}^{x}}-m{{2}^{x}}-m+15>0\) có nghiệm đúng với mọi \(x\in \left[ 1;2 \right]. Tính số phần tử của S

A.  
6
B.  
4
C.  
9
D.  
7
Câu 43: 0.2 điểm

Cho hình lăng trụ đứng ABC.{A}'{B}'{C}'\) có đáy ABC là tam giác đều cạnh bằng a và \(\left( {A}'BC \right)\) hợp với mặt đáy ABC một góc \(30{}^\circ \). Tính thể tích V của khối lăng trụ \(ABC.{A}'{B}'{C}'.

A.  
V=3a38V= \frac{{3{a^3}}}{8}
B.  
V=a338V = \frac{{{a^3}\sqrt 3 }}{8}
C.  
V=a3312V = \frac{{{a^3}\sqrt 3 }}{{12}}
D.  
V=a3324V = \frac{{{a^3}\sqrt 3 }}{{24}}
Câu 44: 0.2 điểm

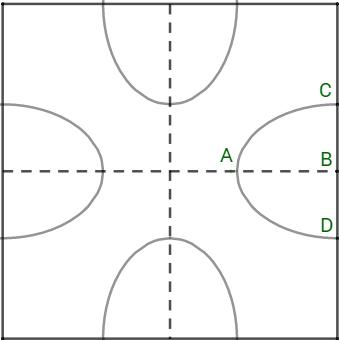
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh 20cm bằng cách khoét đi bốn phần bằng nhau có hình dạng một nửa elip như hình bên. Biết một nửa trục lớn AB=6cm, trục bé CD=8cm. Diện tích bề mặt hoa văn đó bằng

Hình ảnh

A.  
400−48π400 - 48\pi cm2
B.  
400−96π400 - 96\pi cm2
C.  
400−24π400 - 24\pi cm2
D.  
400−36π400 - 36\pi cm2
Câu 45: 0.2 điểm

Trên một cánh đồng có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa 2 cọc là 4 mét còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung.

A.  
2,824m22,824{m^2}
B.  
1,989m21,989{m^2}
C.  
1,034m21,034{m^2}
D.  
1,574m21,574{m^2}
Câu 46: 0.2 điểm

Cho hàm số f\left( x \right)\) liên tục trên R và thỏa \(\int\limits_{0}^{3}{f\left( \sqrt{{{x}^{2}}+16}+x \right)\text{d}x=2019,}\int\limits_{4}^{8}{\frac{f\left( x \right)}{{{x}^{2}}}\text{d}x=1.}\) Tính \(\int\limits_4^8 {f\left( x \right){\rm{d}}x} .

A.  
2019
B.  
4022
C.  
2020
D.  
4038
Câu 47: 0.2 điểm

Cho hàm số f\left( x \right)=\frac{1}{4}{{x}^{4}}-m{{x}^{3}}+\frac{3}{2}\left( {{m}^{2}}-1 \right){{x}^{2}}+\left( 1-{{m}^{2}} \right)x+2019\) với m là tham số thực. Biết rằng hàm số \(y=f\left( \left| x \right| \right)\) có số điểm cực trị lớn hơn 5 khi \(a<{{m}^{2}}<b+2\sqrt{c}\,\left( a,\,b,\,c\,\in \mathbb{R} \right). Tích abc bằng

A.  
8
B.  
6
C.  
16
D.  
18
Câu 48: 0.2 điểm

Cho phương trình: {{2}^{{{x}^{3}}+{{x}^{2}}-2x+m}}-{{2}^{{{x}^{2}}+x}}+{{x}^{3}}-3x+m=0\). Tập các giá trị để bất phương trình có ba nghiệm phân biệt có dạng \(\left( a\,;\,b \right). Tổng a+2b bằng:

A.  
2
B.  
-4
C.  
0
D.  
1
Câu 49: 0.2 điểm

Cho số phức z thỏa mãn \left| z \right|=2\). Tìm giá trị nhỏ nhất của biểu thức \(P=\left| z-4 \right|+2\left| z-3+2i \right|.

A.  
P=25P = 2\sqrt 5
B.  
P=3P = \sqrt 3
C.  
P=42P = 4\sqrt 2
D.  
P=2P = \sqrt 2
Câu 50: 0.2 điểm

Trong không gian với hệ tọa độ Oxyz, cho hai mặt cầu \left( {{S}_{1}} \right),\left( {{S}_{2}} \right)\) lần lượt có phương trình là \({{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-2y-2z-22=0, {{x}^{2}}+{{y}^{2}}+{{z}^{2}}-6x+4y+2z+5=0\). Xét các mặt phẳng \(\left( P \right)\) thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Gọi \(M\left( a;b;c \right)\) là điểm mà tất cả các \(mp\left( P \right) đi qua. Tính tổng S=a+b+c.

A.  
S=−52S = - \frac{5}{2}
B.  
S=52S = \frac{5}{2}
C.  
S=−92S = - \frac{9}{2}
D.  
S=92S = \frac{9}{2}

Xem thêm đề thi tương tự

thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 89THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, được thiết kế để hỗ trợ học sinh ôn luyện các dạng bài quan trọng như hàm số, tích phân, và bài toán thực tế. Tài liệu miễn phí và có đáp án đầy đủ, giúp học sinh chuẩn bị tốt cho kỳ thi Quốc gia.

50 câu hỏi 1 mã đề 1 giờ

101,051 lượt xem 54,411 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 18THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, miễn phí với đáp án chi tiết. Nội dung bao gồm các bài tập trọng tâm như logarit, tích phân, và hình học không gian.

50 câu hỏi 1 mã đề 1 giờ

126,888 lượt xem 68,320 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 7THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, miễn phí và có đáp án đầy đủ. Nội dung bám sát chương trình lớp 12, bao gồm các dạng bài trọng tâm như hàm số, logarit, tích phân, và hình học không gian.

50 câu hỏi 1 mã đề 1 giờ

129,791 lượt xem 69,881 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 30THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, miễn phí và có đáp án đầy đủ. Đề thi bao gồm các bài tập trọng tâm như giải tích, logarit, số phức, và bài toán thực tế.

50 câu hỏi 1 mã đề 1 giờ

124,187 lượt xem 66,864 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 21THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, miễn phí với đáp án chi tiết. Nội dung tập trung vào các dạng bài trọng tâm như hàm số, logarit, tích phân, và hình học không gian, giúp học sinh ôn luyện toàn diện.

50 câu hỏi 1 mã đề 1 giờ

126,135 lượt xem 67,914 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 27THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, miễn phí với đáp án chi tiết. Đề thi bao gồm các dạng bài như hàm số, logarit, và hình học không gian, giúp học sinh chuẩn bị tốt nhất cho kỳ thi.

50 câu hỏi 1 mã đề 1 giờ

124,405 lượt xem 66,983 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 8THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021, miễn phí và có đáp án đầy đủ. Đề thi bao gồm các dạng bài trọng tâm như giải tích, số phức, logarit, và các bài toán thực tế.

50 câu hỏi 1 mã đề 1 giờ

129,177 lượt xem 69,552 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 99THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021 với các câu hỏi trọng tâm về logarit, tích phân, và hình học không gian. Tài liệu này là công cụ hữu ích để học sinh ôn tập hiệu quả và đạt kết quả cao trong kỳ thi.

50 câu hỏi 1 mã đề 1 giờ

98,284 lượt xem 52,920 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 44THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021 với các dạng bài quan trọng như logarit, số phức, và bài toán thực tế. Đề thi bám sát chương trình lớp 12, miễn phí với đáp án chi tiết, là tài liệu ôn luyện hiệu quả giúp học sinh tự tin bước vào kỳ thi.

50 câu hỏi 1 mã đề 1 giờ

120,351 lượt xem 64,799 lượt làm bài

Chưa chinh phục!!!
thumbnail
Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 59THPT Quốc giaToán
Đề thi thử THPT Quốc gia môn Toán năm 2021 với nội dung được thiết kế bám sát chương trình lớp 12. Đề thi bao gồm các dạng bài tập trọng tâm như hàm số, số phức, và bài toán thực tế, là tài liệu luyện thi hiệu quả giúp học sinh tự tin bước vào kỳ thi.

50 câu hỏi 1 mã đề 1 giờ

111,161 lượt xem 59,850 lượt làm bài

Chưa chinh phục!!!