Trang chủ Đề thi Lớp 9 Toán 12103
thumbnail

Trắc nghiệm Toán 9 Chương 3 Bài 4 (Nhận biết): Góc tạo bởi tia tiếp tuyến và dây cung (Có đáp án)

Củng cố kiến thức cơ bản với bài trắc nghiệm Toán 9 Chương 3 Bài 4 (Nhận biết) về góc tạo bởi tia tiếp tuyến và dây cung. Đề thi giúp học sinh nhận diện các tính chất quan trọng, nắm vững định nghĩa và hiểu cách xác định góc trong đường tròn. Phù hợp để ôn tập trước kiểm tra và rèn luyện kỹ năng giải bài toán hình học. Làm bài miễn phí, có đáp án chi tiết để đối chiếu kết quả.

Từ khoá: trắc nghiệm Toán 9 góc tiếp tuyến và dây cung bài tập nhận biết chương 3 hình học 9 kiểm tra Toán 9 đề thi có đáp án ôn tập Toán lớp 9 góc với đường tròn bài tập hình học 9

Số câu hỏi: 5 câuSố mã đề: 1 đềThời gian: 1 giờ

157,422 lượt xem 12,103 lượt làm bài


Bạn chưa làm đề thi này!!!

 

Xem trước nội dung:

Câu 1: 2 điểm

Góc ở hình nào dưới đây biểu diễn góc tạo bởi tiếp tuyến và dây cung?

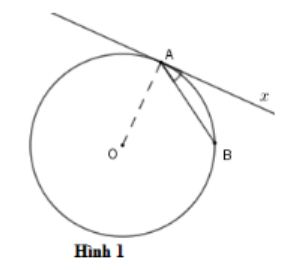
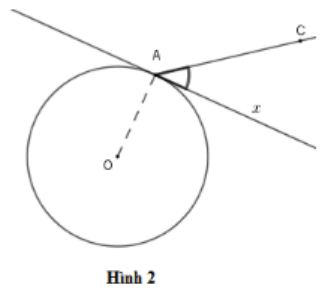
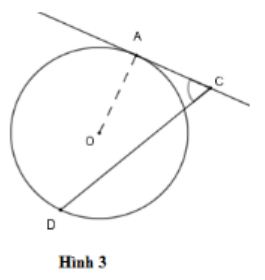
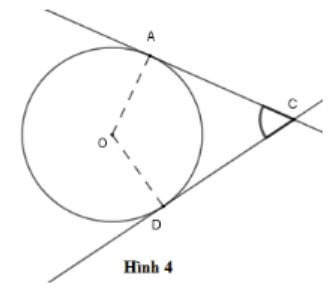
Hình ảnhHình ảnh

Hình ảnhHình ảnh

A.  
Hình 1
B.  
Hình 2
C.  
Hình 3
D.  
Hình 4
Câu 2: 2 điểm

Trong hình vẽ dưới đây, biết CF là tiếp tuyến của đường tròn (O). Hãy chỉ ra góc tạo bởi tiếp tuyến và dây cung?

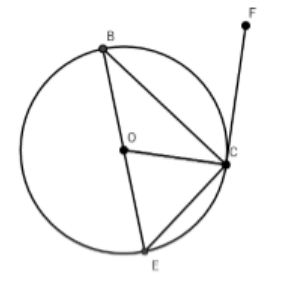
Hình ảnh

A.  
B C O ^
B.  
B C F ^
C.  
C O E ^
D.  
B E C ^
Câu 3: 2 điểm

Góc tạo bởi tiếp tuyến và dây cung có số đo bằng?

A.  
90o
B.  
Số đo góc ở tâm chắn cung đó
C.  
Nửa số đo của góc nội tiếp chắn cung đó
D.  
Nửa số đo cung bị chắn
Câu 4: 2 điểm

Kết luận nào sau đây là đúng?

A.  
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo lớn hơn số đo góc nội tiếp chắn cung đó
B.  
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo nhỏ hơn số đo góc nội tiếp chắn cung đó
C.  
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau
D.  
Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung có số đo bằng hai lần số đo của góc nội tiếp chắn cung đó
Câu 5: 2 điểm

So sánh A P B ^ và A B T ^ trong hình vẽ dưới đây biết BT là tiếp tuyến của đường tròn (O)

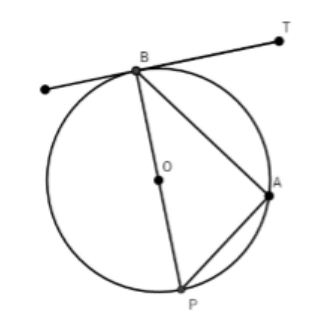
Hình ảnh

A.  
A B T ^   =   A P B ^
B.  
A B T ^   =   1 2 A P B ^
C.  
A B T ^   <   A P B ^
D.  
A B T ^   >   A P B ^

Đề thi tương tự

Trắc nghiệm Toán 9 Chương 3 Bài 4: Tính chất góc tạo bởi tia tiếp tuyến và dây cung (Có đáp án)

1 mã đề 5 câu hỏi 1 giờ

169,268 xem13,007 thi

Trắc nghiệm Toán 9 Chương 3 Bài 4 (Thông hiểu): Góc tạo bởi tia tiếp tuyến và dây cung (Có đáp án)

1 mã đề 10 câu hỏi 1 giờ

181,571 xem13,958 thi

Trắc nghiệm Bài tập Toán 4 Chương 3 Dấu hiệu chia hết cho 9 có đáp án

3 mã đề 60 câu hỏi 1 giờ

175,105 xem13,463 thi

Trắc nghiệm Toán 9 - Chương 3, Bài 1: Hệ hai phương trình bậc nhất hai ẩn (Nhận biết)

1 mã đề 10 câu hỏi 1 giờ

189,346 xem14,557 thi

Trắc nghiệm Toán 9 Bài 8: Bài tập ôn tập Chương 3

1 mã đề 27 câu hỏi 1 giờ

172,926 xem13,295 thi

Trắc nghiệm Toán 9 - Chương 2: Đường tròn - Bài 2: Đường kính và dây của đường tròn (Thông hiểu)

1 mã đề 5 câu hỏi 1 giờ

149,739 xem11,514 thi

Tổng hợp Trắc nghiệm Toán 9 Chương 2 Đại Số 9 (có đáp án)

1 mã đề 31 câu hỏi 1 giờ

190,773 xem14,668 thi

Tổng hợp Trắc nghiệm Toán 9 Chương 1 Đại Số 9 (có đáp án)

1 mã đề 35 câu hỏi 1 giờ

168,166 xem12,930 thi

Tổng hợp bài tập trắc nghiệm Toán 9 Chương 2 Hình học 9 (có đáp án)

1 mã đề 40 câu hỏi 1 giờ

154,662 xem11,887 thi