Trắc nghiệm Ứng dụng của tích phân có đáp án

Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x = 1 và x = 3, biết rằng khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x $\left(1\le x\le 3\right)$thì được thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và $\sqrt{3x^2-2}$

Thể tích vật thể nằm giữa hai mặt phẳng x = 0 và x = 2, biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x $\left(0\le x\le 2\right)$là một nửa đường tròn đường kính bằng:

Cho hình phẳng giới hạn bởi $D=\left\{y=\tan x; y=0; x=0; x=\frac{\mathrm{\pi }}{3}\right\}$. Thể tích vật tròn xoay khi D quay quanh trục Ox là: $V=\mathrm{\pi }\left(\mathrm{a}-\frac{\mathrm{\pi }}{\mathrm{b}}\right)$với $a,b\in R$. Tính $T=a^2+2b$

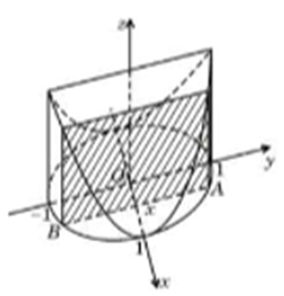
Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình $x^2+y^2=1$và mỗi thiết diện vuông góc với trục Ox là một hình vuông (tham khảo hình bên)

Cho hình phẳng (H) giới hạn bởi parabol $y=a{x}^2+1(a>0),$trục tung và đường thẳng x = 1. Quay (H) quanh trục Ox được một khối tròn xoay có thể tích bằng $\frac{28}{15}\mathrm{\pi }$. Mệnh đề nào dưới đây đúng?

Thể tích của vật tròn xoay có được khi quay hình phẳng giới hạn bởi đồ thị hàm y=tanx, trục Ox, đường thẳng x = 0, đường thẳng $x=\frac{\mathrm{\pi }}{3}$quanh trục Ox là:

Tính thể tích khi $S=\left\{y=x^2-4x+6 ;y=-x^2-2x+6\right\}$quay quanh trục Ox

Gọi H là hình phẳng giới hạn bởi parabol $y=x^2$và đường thẳng y = 2x. Tính thể tích V của khối tròn xoay tạo thành khi quay hình (H) quanh trục hoành

Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a; b] với a < b. Kí hiệu $S_1$là diện tích hình phẳng giới hạn bởi các đường y = 3f(x), y = 3g(x), x = a, x = b, $S_2$là diện tích hình phẳng giới hạn bởi các đường y = f(x) − 2, y = g(x) − 2, x = a, x = b. Khẳng định nào sau đây đúng?

Thể tích khối tròn xoay sinh ra bởi phép quay xung quanh Ox của hình giới hạn bởi trục Ox và parabol (P): $y=x^2–ax$(a>0) bằng V = 2. Khẳng định nào dưới đây đúng?

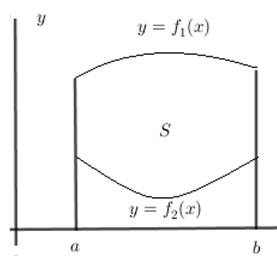
Cho hai hàm số $y=f_1\left(x\right)$và $y=f_2\left(x\right)$liên tục trên đoạn [a;b] và có đồ thị như hình vẽ bên. Gọi S là hình phẳng giới hạn bởi hai đồ thị trên và các đường thẳng x = a, x = b. Thể tích V của vật thể tròn xoay tạo thành khi quay S quanh trục Ox được tính bởi công thức nào sau đây?

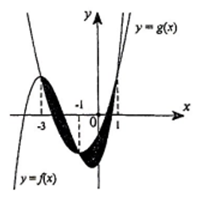
Cho hai hàm số $f\left(x\right)=m{x}^3+n{x}^2+px-\frac{5}{2}$(m, n, p thuộc R) và $g\left(x\right)=x^2+2x-1$có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là −3; −1; 1( tham khảo hình vẽ bên). Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số f(x)và g(x) bằng

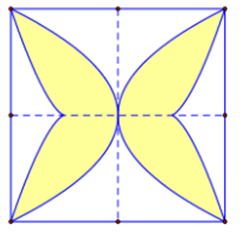
Sàn của một viện bảo tàng mỹ thuật được lát bằng những viên gạch hình vuông cạnh 40(cm) như hình bên. Biết rằng người thiết kế đã sử dụng các đường cong có phương trình $4x^2=y^4$và $4\left(\right|x|-1{)}^3=y^2$để tạo hoa văn cho viên gạch. Diện tích phần màu vàng gần nhất với giá trị nào dưới đây?

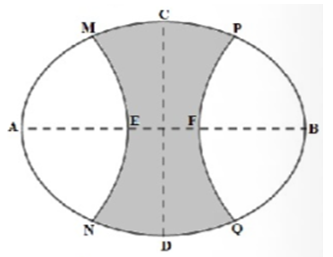
Cho hàm số $y=x^4-3x^2+m$có đồ thị là $\left(C_m\right)$(m là tham số thực). Giả sử $\left(C_m\right)$cắt trục Ox tại 4 điểm phân biệt. Gọi $S_1, S_2$là diện tích của hai hình phẳng nằm dưới trục Ox và $S_3$là diện tích của hình phẳng nằm trên trục Ox được tạo bởi $\left(C_m\right)$với trục Ox. Biết rằng tồn tại duy nhất giá trị $m=\frac{a}{b}$(với a, b thuộc N* và tối giản) để $S_1 + S_2 = S_3$. Giá trị của 2a − b bằng:

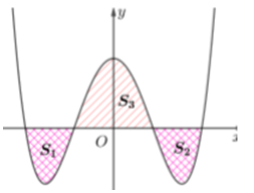
Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là $S_1$và $S_2$(tham khảo hình vẽ).

Tỉ số $\frac{S_1}{S_2}$bằng:

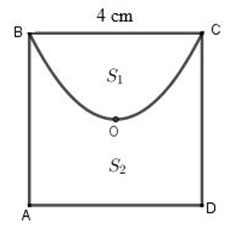
Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh A, B, C, D và hai đường parabol có các đỉnh lần lượt là E, F (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng AB, đối xứng với nhau qua trục CD, hai parabol cắt elip tại các điểm M, N, P, Q. Biết AB = 8m, CD = 6m, $MN = PQ = 3\sqrt{3}m$, EF = 2m. Chi phí để trồng hoa trên vườn là $300.000đ/m^2$. Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây

Cho hàm số y = f(x) liên tục trên R và thỏa mãn f(−1) > 0 > f(0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = f(x), y = 0, x = 1 và x = −1. Mệnh đề nào sau đây là đúng?

Cho parabol (P) có đồ thị như hình vẽ:

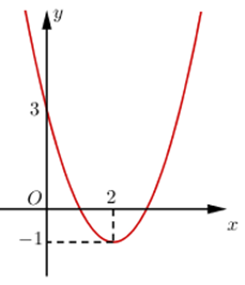
Tính diện tích giới hạn bởi (P) và trục hoành.

Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số $y=x^2-2x$và $y=-x^2+4x$

Tính diện tích hình phẳng giới hạn bởi hai đường: $y=|x^2-4x+3|;y=x+3$

Gọi(H)là hình phẳng giới hạn bởi đồ thị hàm số $y=x^2-4x+4$, trục tung, trục hoành. Giá trị củakđể đường thẳngd đi qua A (0; 4) có hệ số góck chia(H)  thành 2 phần có diện tích bằng nhau là

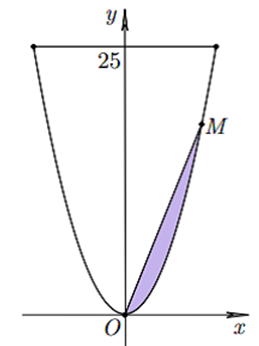
Ông B có một khu vườn giới hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxy như hình vẽ bên thì parabol có phương trình $y=x^2$và đường thẳng là y = 25. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua O và điểm M trên parabol để trồng hoa. Hãy giúp ông B xác định điểm M bằng cách tính độ dài OM để diện tích mảnh vường nhỏ bằng 92.

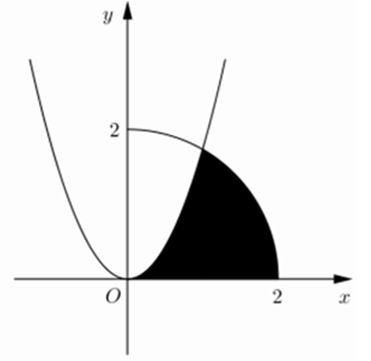
Cho (H) là hình phẳng giới hạn bởi parabol $y=\sqrt{3}{x}^2$, cung tròn có phương trình $y=\sqrt{4-x^2}$(với 0 ≤ x ≤ 2) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của (H) bằng

Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $y=-x^2+2x+1$và $y=2x^2-4x+1$là:

Diện tích S của hình phẳng giới hạn bởi các đường $y=-x^2+2x,y=-3,x=1,x=2$được tính bởi công thức nào dưới đây?