Trang chủ Hỏi & đáp THPT Quốc gia Vật lý Câu hỏi số #151

Đặt điện áp xoay chiều u=200 2 cos100πt (V) vào hai đầu mạch điện gồm cuộn dây không thuần cảm và biến trở R mắc nối tiếp. Giản đồ véc tơ quay mô tả điện áp tức thời trên cuộn dây, biến trở R và hai đầu mạch lần lượt là U → d ; U → R và U → được biểu diễn như hình vẽ. Thay đổi R để diện tích tam giác tạo bởi ba véc tơ U → d ; U → R và U → có giá trị lớn nhất thì thu được giá trị lớn nhất đó là 10 4 3 3 V 2 và lúc đó R= 200 3 3 (Ω) . Thay đổi R để công suất tiêu thụ trên cả mạch lớn nhất thì công suất lớn nhất đó là bao nhiêu?

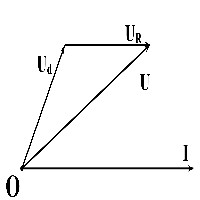
Hình ảnh

A.  

100 3 3 W .

B.  

100 W .

C.  

100 3 W .

D.  

200 W .

Đáp án đúng là: D

Khi R thay đổi thì tan(φ)rL=ZLr=const⇒(φ)rL=const⇒∠OMB=consttan \left(\varphi\right)_{r L} = \dfrac{Z_{L}}{r} = c o n s t \Rightarrow \left(\varphi\right)_{r L} = c o n s t \Rightarrow \angle O M B = c o n s t
⇒\RightarrowM luôn nhìn OB dưới 1 góc không đổi nên quỹ tích điểm M nằm trên cung nhỏ OB⌢\overset{⌢}{O B}
SOMB=12.200.MHS_{O M B} = \dfrac{1}{2} . 200 . M H max khi MHmax⇒MM H_{max} \Rightarrow M nằm chính giữa cung nhỏ OB⌢\overset{⌢}{O B} ⇒ΔOMB\Rightarrow \Delta O M B cân tại M
→(10)433=12..200.MHmax⇒MHmax=1003\rightarrow \dfrac{\left(10\right)^{4} \sqrt{3}}{3} = \dfrac{1}{2} . . 200 . M H_{max} \Rightarrow M H_{max} = \dfrac{100}{\sqrt{3}} và tanα=MHHB=100/3100⇒α=(30)otan \alpha = \dfrac{M H}{H B} = \dfrac{100 / \sqrt{3}}{100} \Rightarrow \alpha = \left(30\right)^{o}


I=URR=2003/32003/3=1A→ZL=ULI=100ΩI = \dfrac{U_{R}}{R} = \dfrac{200 \sqrt{3} / 3}{200 \sqrt{3} / 3} = 1 A \rightarrow Z_{L} = \dfrac{U_{L}}{I} = 100 \Omega
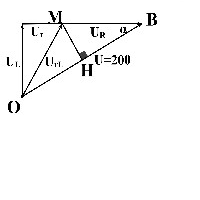
Chú ý: Đề chưa chặt chẽ, ta ngầm hiểu độ dài vectơ là giá trị hiệu dụng chứ không phải cực đại


 

Câu hỏi tương tự:

#4932 THPT Quốc giaVật lý

Đặt điện áp xoay chiều u=200 2 cos100πt vào hai đầu một đoạn mạch gồm cuộn cuộn thuần có độ tự cảm L= 1 π H và tụ điện có điện dung C= 10 - 4 2 π F mắc nối tiếp. Cường độ dòng điện hiệu dụng trong đoạn mạch là

Lượt xem: 83,875 Cập nhật lúc: 22:27 21/11/2024

#6223 THPT Quốc giaVật lý

Đặt điện áp xoay chiều u=200 2 cos100πt (V) vào hai đầu một đoạn mạch gồm điện trở thuần 100Ω , cuộn cảm thuần và tụ điện mắc nối tiếp. Điện áp ở hai đầu tụ điện là u C =100 2 cos 100 π t - π 2 V . Công suất tiêu thụ điện của đoạn mạch là

Lượt xem: 105,822 Cập nhật lúc: 04:46 22/11/2024

#2364 THPT Quốc giaVật lý

Đặt điện áp xoay chiều u=200 2 cos 100 π t - π 3 (V) vào hai đầu đoạn mạch RLC nối tiếp. Biết R=100Ω , cuộn dây thuần cảm có độ tự cảm L có giá trị thay đổi được, tụ điện có điện dung C= 10 - 4 π F . Điều chỉnh L để công suất tiêu thụ của mạch đạt giá trị cực đại. Biểu thức của điện áp hai đầu tụ điện lúc đó là

Lượt xem: 40,219 Cập nhật lúc: 08:59 21/11/2024

#2339 THPT Quốc giaVật lý

Đặt điện áp xoay chiều u=200 2 cos 100 π t + π 6 V vào mạch điện chỉ có tụ điện. Cường độ dòng điện chạy qua mạch có pha ban đầu bằng

Lượt xem: 39,832 Cập nhật lúc: 00:03 22/11/2024

#548 THPT Quốc giaVật lý

Đặt một điện áp xoay chiều u=200 2 cos100πt (V) vào hai đầu đoạn mạch có điện trở R , tụ điện C mắc nối tiếp thì điện áp hiệu dụng giữa hai đầu điện trở là u R =100 2 cos(100πt+φ)(V) . Giá trị của φ là

Lượt xem: 9,344 Cập nhật lúc: 19:07 21/11/2024

#668 THPT Quốc giaVật lý

Mạch điện xoay chiều gồm RLC mắc nối tiếp, có R=100Ω, Z C =100Ω, Z L =200Ω . Đặt vào 2 đầu mạch một điện áp xoay chiều u=200 2 cos 100 π t - π 6 (V) . Biểu thức dòng điện qua mạch là:

Lượt xem: 11,410 Cập nhật lúc: 16:36 21/11/2024

#5220 THPT Quốc giaVật lý

Cho mạch điện xoay chiều AB có các phần tử nối tiếp theo thứ tự: R,C và cuộn dây thuần cảm có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u=200 2 cos100πt (V) . Khi L= L 1 = 1 π H hoặc L= L 2 = 3 π H thì cường độ dòng điện trong mạch có giá trị hiệu dụng bằng nhau và bằng 2 A . Điện áp hiệu dụng U R C giữa hai đầu đoạn mạch chứa R và C bằng

Lượt xem: 88,808 Cập nhật lúc: 03:59 22/11/2024

#6379 THPT Quốc giaVật lý

Mạch điện xoay chiều AB gồm AM có một điện trở thuần R nối trực tiếp với cuộn cảm thuần độ tự cảm L=318(mH) . MB chỉ có tụ điện có điện dung C, thay đổi được. Điện áp tức thời giữa hai mạch AB là u=200 2 cos100πt (V) . Khi điều chỉnh C, điện áp hiệu dụng hai đầu cuộn dây đạt giá trị cực đại bằng 100 2 ( V) . Giá trị R gần nhất với giá trị nào sau đây?

Lượt xem: 108,502 Cập nhật lúc: 01:12 22/11/2024

#1327 THPT Quốc giaVật lý

Đặt điện áp xoay chiều u=200 2 cos(100πt)V vào hai đầu đoạn mạch chỉ có tụ điện với điện dung bằng 10 - 4 π F . Cường độ dòng điện hiệu dụng qua tụ điện là

Lượt xem: 22,612 Cập nhật lúc: 20:39 21/11/2024


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN VẬT LÝ - THPT Chuyên ĐH Vinh.docxTHPT Quốc giaVật lý

1 mã đề 40 câu hỏi 50 phút

1,874 lượt xem 973 lượt làm bài