Trang chủ   Hỏi & đáp   THPT Quốc gia   Toán   Câu hỏi số #8864  

Cho hàm số f(x)f \left( x \right) có f′′(0)=−81100f^{''} \left( 0 \right) = - \dfrac{81}{100} và đồ thị của hàm số y=f′(x)y = f^{'} \left( x \right) như hình bên dưới.



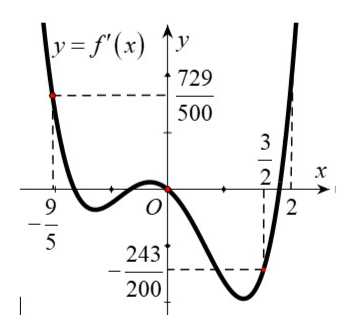
Hỏi hàm số y=∣f(x)+81200x2−m∣y = \left|\right. f \left( x \right) + \dfrac{81}{200} x^{2} - m \left|\right., ( mm là tham số) có nhiều nhất bao nhiêu điểm cực trị trên nửa khoảng (−95;2]\left(\right. - \dfrac{9}{5} ; 2 \left]\right.?

A.  

4.

B.  

5.

C.  

6.

D.  

3.

Đáp án đúng là: D

Giải thích đáp án:

Xét hàm số g(x)=f(x)+81200x2−mg \left( x \right) = f \left( x \right) + \dfrac{81}{200} x^{2} - m ⇒g′(x)=f′(x)+81100x\Rightarrow g^{'} \left( x \right) = f^{'} \left( x \right) + \dfrac{81}{100} x.
g′(x)=0g^{'} \left( x \right) = 0 ⇔f′(x)+81100x=0\Leftrightarrow f^{'} \left( x \right) + \dfrac{81}{100} x = 0 ⇔f′(x)=−81100x\Leftrightarrow f^{'} \left( x \right) = - \dfrac{81}{100} x (1)
Do f′′(0)=−81100,f^{''} \left( 0 \right) = - \dfrac{81}{100} , f′(0)=0f^{'} \left( 0 \right) = 0 nên phương trình tiếp tuyến với đồ thị hàm số y=f′(x)y = f^{'} \left( x \right) tại gốc tọa độ là y=f′′(0)(x−0)+f′(0)y = f^{''} \left( 0 \right) \left( x - 0 \right) + f^{'} \left( 0 \right) ⇔y=−81100x\Leftrightarrow y = - \dfrac{81}{100} x.
Tiếp tuyến này qua các điểm O(0;0)O \left( 0 ; 0 \right), A(−95;729500)A \left( - \dfrac{9}{5} ; \dfrac{729}{500} \right), B(32;−243200)B \left( \dfrac{3}{2} ; - \dfrac{243}{200} \right) và O(0;0)O \left( 0 ; 0 \right) là tiếp điểm.
Phương trình (1) là phương trình hoành độ giao điểm của đồ thị hàm số y=f′(x)y = f^{'} \left( x \right) và tiếp tuyến y=−81100xy = - \dfrac{81}{100} x.



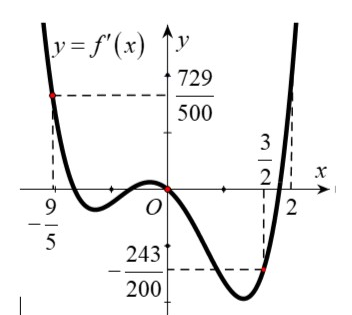
Dựa vào đồ thị ta thấy (1) có ba nghiệm x=−95, x=0, x=32x = - \dfrac{9}{5} , \textrm{ } x = 0 , \textrm{ } x = \dfrac{3}{2}, nên bảng biến thiên của hàm số g(x)g \left( x \right) trên nửa khoảng (−95;2]\left(\right. - \dfrac{9}{5} ; 2 \left]\right. là
xx −92- \dfrac{9}{2} 0 32\dfrac{3}{2} 2
g′(x)g^{'} \left( x \right) − 0 − 0 ++
g(x)g \left( x \right)

Trên nửa khoảng (−95;2],\left(\right. - \dfrac{9}{5} ; 2 \left]\right. , đồ thị hàm số g(x)=f(x)+81200x2−mg \left( x \right) = f \left( x \right) + \dfrac{81}{200} x^{2} - m có 1 cực trị và cắt trục hoành tối đa 2 điểm nên hàm số y=∣g(x)∣=∣f(x)+81200x2−m∣y = \left|\right. g \left( x \right) \left|\right. = \left|\right. f \left( x \right) + \dfrac{81}{200} x^{2} - m \left|\right. có nhiều nhất là 2+1=32 + 1 = 3 điểm cực trị trên nửa khoảng (−95;2].\left(\right. - \dfrac{9}{5} ; 2 \left]\right. .

Câu hỏi tương tự:

#7563 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right)có và đồ thị của hàm số y=f′(x)y = f ' \left( x \right) như hình bên dưới



Hỏi hàm số y=∣f(x)+81200x2−m∣y = \left|\right. f \left( x \right) + \dfrac{81}{200} x^{2} - m \left|\right., ( mmlà tham số) có nhiều nhất bao nhiêu điểm cực trị trên nửa khoảng (−95;2]?\left(\right. - \dfrac{9}{5} ; 2 \left]\right. ?

Lượt xem: 128,599 Cập nhật lúc: 06:38 31/07/2024

#8338 THPT Quốc giaToán

Cho hàm số y=2xx+1y = \dfrac{2 x}{x + 1} có đồ thị (C)\left( C \right) và điểm A(0; a)A \left( 0 ; \textrm{ } a \right). Gọi SS là tập hợp tất cả các giá trị thực của aa để từ AA kẻ được hai tiếp tuyến AM, ANA M , \textrm{ } A N đến (C)\left( C \right) với M, NM , \textrm{ } N là các tiếp điểm và MN=4.M N = 4 . Tổng tất cả các phần tử của SS bằng

Lượt xem: 141,789 Cập nhật lúc: 14:31 31/07/2024

#8683 THPT Quốc giaToán

Cho hàm số y=x3−3x+2y = x^{3} - 3 x + 2 có đồ thị là (C)\left( C \right). Số giao điểm của (C)\left( C \right) và trục hoành là

Lượt xem: 147,628 Cập nhật lúc: 13:16 02/08/2024

#11384 THPT Quốc giaToán

Cho đồ thị hàm số y=f(x)y = f \left( x \right) liên tục trên R\mathbb{R} và có đồ thị như hình vẽ.



Số nghiệm của phương trình ∣2f(x)−3∣=1\left|\right. 2 f \left( x \right) - 3 \left|\right. = 1 là

Lượt xem: 193,540 Cập nhật lúc: 01:43 30/08/2024

#7949 THPT Quốc giaToán

Cho hàm số

liên tục trên đoạn

và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình

trên đoạn

là

Lượt xem: 135,151 Cập nhật lúc: 17:16 03/08/2024

#8248 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) có đạo hàm liên tục trên đoạn [−3;3]\left[\right. - 3 ; 3 \left]\right. và đồ thị như hình vẽ bên. Giá trị nhỏ nhất của hàm số trên đoạn [−3;3]\left[\right. - 3 ; 3 \left]\right. là:

Lượt xem: 140,231 Cập nhật lúc: 02:08 31/07/2024

#7567 THPT Quốc giaToán

Cho hàm số y=x+1x−1y = \dfrac{x + 1}{x - 1} có đồ thị (C)\left( C \right). Gọi AA, BB là hai điểm thuộc hai nhánh của (C)\left( C \right) và các tuyến tiếp của (C)\left( C \right) tại AA, BB cắt các đường tiệm cận ngang và đứng của (C)\left( C \right) lần lượt tại các điểm MM, NN, PP, QQ. Diện tích tứ giác MNPQM N P Q có giá trị nhỏ nhất bằng?

Lượt xem: 128,660 Cập nhật lúc: 20:06 01/08/2024

#8822 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) liên tục trên R\mathbb{R} và có đồ thị hàm số y=f′(x)y = f^{'} \left( x \right) như hình vẽ dưới đây.



Tìm tất cả các giá trị nguyên của tham số mm thuộc đoạn [−10;10]\left[\right. - 10 ; 10 \left]\right.để hàm số g(x)=f(x−m)−12(x−m+1())2+2024g \left( x \right) = f \left( x - m \right) - \dfrac{1}{2} \left( x - m + 1 \left(\right)\right)^{2} + 2024 đồng biến trên (1;2)\left( 1 ; 2 \right).

Lượt xem: 150,003 Cập nhật lúc: 16:59 31/07/2024

#8112 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) liên tục trên đoạn [−1;5]\left[\right. - 1 ; 5 \left]\right. và có đồ thị trên đoạn [−1;5]\left[\right. - 1 ; 5 \left]\right. như hình vẽ bên. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f (x)f \text{ } \left( x \right) trên đoạn [−1;5]\left[\right. - 1 ; 5 \left]\right. bằng


Lượt xem: 137,920 Cập nhật lúc: 22:27 30/07/2024


Đề thi chứa câu hỏi này:

34. Đề thi thử TN THPT môn Toán năm 2024 - THPT HẬU LỘC 2 - TH.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,773 lượt xem 2,548 lượt làm bài