Cho hàm số
có đạo hàm
. Hàm số
liên tục trên tập số thực
và có đồ thị như hình vẽ.
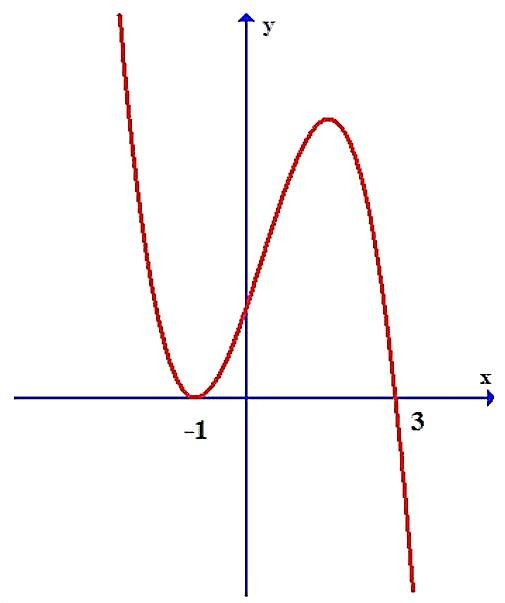
Biết
. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
trên
bằng
A.
.
B.
.
C. 488 .
D.
.
Đáp án đúng là: A
Cho hàm số
có đạo hàm
. Hàm số
liên tục trên tập số thực
và có đồ thị như hình vẽ.

Biết . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên bằng
.
.
488 .
.
Đáp án đúng là: A
Từ đồ thị hàm số
và giả thiết
ta có bảng biến thiên hàm số
trên
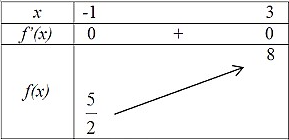
Ta có nên .
Xét trên đoạn .
do .
Bảng biến thiên

;
Câu hỏi tương tự:
#8358 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên
và có đồ thị hàm số
như hình vẽ
Có bao nhiêu giá trị nguyên của để hàm số có 3 điểm cực trị dương?
Lượt xem: 142,248 Cập nhật lúc: 16:23 24/04/2025
#8264 THPT Quốc giaToán
Cho hàm số
có đạo hàm, liên tục trên
và thỏa mãn
Tích phân
bằng
Lượt xem: 140,561 Cập nhật lúc: 16:05 25/04/2025
#8245 THPT Quốc giaToán
Cho hàm số có đạo hàm, liên tục trên và thỏa mãn . Tích phân bằng
Lượt xem: 140,248 Cập nhật lúc: 11:54 24/04/2025
#8221 THPT Quốc giaToán
Cho hàm số
có đạo hàm cấp hai liên tục trên
, biết rằng
và hàm số
là hàm số bậc ba có đồ thị như hình vẽ.
Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đồ thị hàm số , khi quay quanh trục có giá trị nằm trong khoảng nào sau đây?
Lượt xem: 139,871 Cập nhật lúc: 13:37 23/04/2025
#8658 THPT Quốc giaToán
Cho hàm số
có
có đạo hàm liên tục trên
và bảng xét dấu đạo hàm như sau
Hàm số có bao nhiêu điểm cực trị?
Lượt xem: 147,359 Cập nhật lúc: 19:07 23/04/2025
#8936 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên
. Đồ thị hàm số
như hình vẽ sau:
Số điểm cực trị của hàm số là:
Lượt xem: 152,017 Cập nhật lúc: 04:50 23/04/2025
#8153 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên đoạn
và thỏa mãn
.
Giả sử rằng
là một nguyên hàm của hàm số
trên
. Tích phân
bằng
Lượt xem: 138,758 Cập nhật lúc: 19:37 25/04/2025
#8226 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên thoả mãn và . Tính .Lượt xem: 140,012 Cập nhật lúc: 02:20 23/04/2025
#8248 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên đoạn
và đồ thị như hình vẽ bên. Giá trị nhỏ nhất của hàm số trên đoạn
là:
Lượt xem: 140,320 Cập nhật lúc: 21:54 24/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
4,571 xem342 thi
