Cho hàm số
xác định trên
\mathbb{R} \left{ 1 \right} liên tục trên mỗi khoảng xác định và có bảng biến thiên sau.
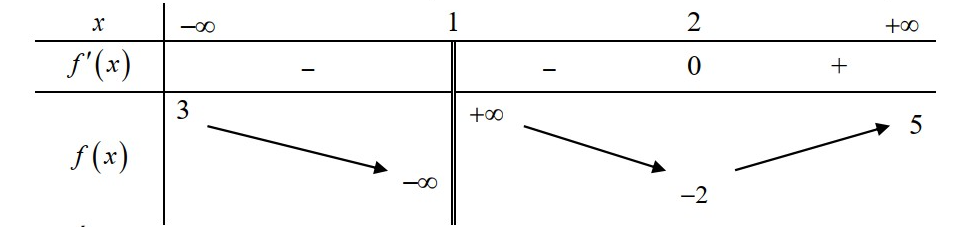
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: A
Cho hàm số
xác định trên
\mathbb{R} \left{ 1 \right} liên tục trên mỗi khoảng xác định và có bảng biến thiên sau.

Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
.
.
.
.
Đáp án đúng là: A
Cho hàm số
xác định trên
liên tục trên mỗi khoảng xác định và có bảng biến thiên sau.
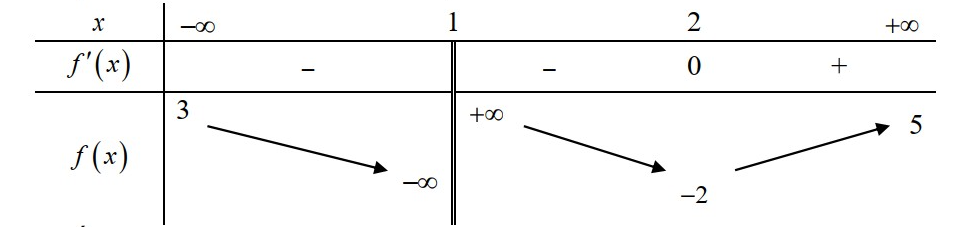
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A. . B. . C. . D. .
Lời giải
Vì nên đồ thị hàm số có một tiệm cận ngang là đường thẳng .
nên đồ thị hàm số có một tiệm cận ngang là đường thẳng .
và nên đồ thị hàm số có một tiệm cận đứng là đường thẳng .
Vậy hàm số có đường tiệm cận.
Câu hỏi tương tự:
#8074 THPT Quốc giaToán
Cho hàm số
xác định trên
, liên tục trên các khoảng xác định của nó và có bảng biến thiên như hình vẽ:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:
Lượt xem: 137,383 Cập nhật lúc: 13:48 14/05/2025
#8866 THPT Quốc giaToán
Cho hàm số
xác định và liên tục trên khoảng
có bảng biến thiên như hình sau:
Mệnh đề nào sau đây đúng?
Lượt xem: 150,914 Cập nhật lúc: 04:10 15/05/2025
#8173 THPT Quốc giaToán
Cho hàm số
xác định và liên tục trên đoạn
và có đồ thị như hình vẽ. Biết rằng diện tích hình phẳng
giới hạn bởi đồ thị hàm số
và đường cong
lần lượt là
Tích phân
bằng
Lượt xem: 139,117 Cập nhật lúc: 04:34 17/05/2025
#7827 THPT Quốc giaToán
Cho hàm số xác định và liên tục trên có và . Hàm số có bao nhiêu điểm cực trị ?
Lượt xem: 133,236 Cập nhật lúc: 05:40 09/05/2025
#8120 THPT Quốc giaToán
Cho hàm số
xác định và liên tục trên đoạn
. Biết diện tích hình phẳng
giới hạn bởi đồ thị hàm số
và đường thẳng
lần lượt là
. Tính tích phân
bằng?
Lượt xem: 138,216 Cập nhật lúc: 22:52 13/05/2025
#8562 THPT Quốc giaToán
Cho hàm số xác định và liên tục trên đoạn . Diện tích hình phằng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng được tính theo công thức
Lượt xem: 145,741 Cập nhật lúc: 23:02 12/05/2025
#8076 THPT Quốc giaToán
Cho hàm số
xác định và liên tục trên
và có bảng biến thiên như sau:
Mệnh đề nào sau đây là đúng?
Lượt xem: 137,410 Cập nhật lúc: 22:11 14/05/2025
#8240 THPT Quốc giaToán
Cho hàm số
xác định, liên tục trên
và có bảng biến thiên như sau
Giá trị cực đại của hàm số đã cho là
Lượt xem: 140,241 Cập nhật lúc: 05:41 14/05/2025
#8336 THPT Quốc giaToán
Cho hàm số
xác định, liên tục trên đoạn
và có đồ thị là đường cong trong hình vẽ.
Hỏi trên đoạn hàm số có bao nhiêu điểm cực trị?
Lượt xem: 141,821 Cập nhật lúc: 07:44 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
407 xem25 thi
