Cho hàm số
liên tục trên
, đồ thị hàm số
được cho như hình vẽ dưới đây.
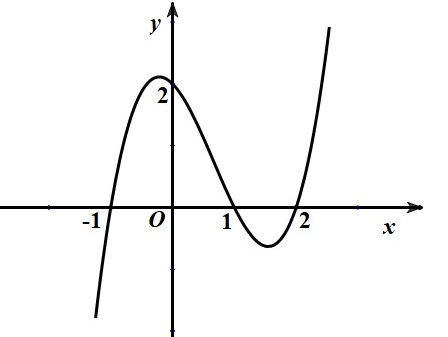
Hàm số
đồng biến trên khoảng nào dưới đây?
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: A
Cho hàm số
liên tục trên
, đồ thị hàm số
được cho như hình vẽ dưới đây.

Hàm số đồng biến trên khoảng nào dưới đây?
.
.
.
.
Đáp án đúng là: A
Cho hàm số
liên tục trên
, đồ thị hàm số
được cho như hình vẽ dưới đây.
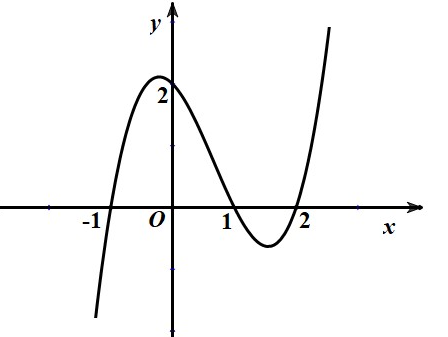
Hàm số đồng biến trên khoảng nào dưới đây?
A. . B. . C. . D. .
Lời giải
Ta có: . Suy ra
Ta có bảng xét dấu của
![]()

Từ bảng xét dấu ta thấy hàm số đồng biến trên khoảng .
Câu hỏi tương tự:
#8822 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có đồ thị hàm số
như hình vẽ dưới đây.
Tìm tất cả các giá trị nguyên của tham số thuộc đoạn để hàm số đồng biến trên .
Lượt xem: 150,096 Cập nhật lúc: 21:13 13/05/2025
#8844 THPT Quốc giaToán
Cho hàm số liên tục trên và thỏa mãn . Đồ thị hàm số cắt đồ thị hàm số tại 3 điểm có hoành độ là . Hình phẳng giới hạn bởi đồ thị hai hàm số và có diện tích bằng
Lượt xem: 150,531 Cập nhật lúc: 04:22 17/05/2025
#8330 THPT Quốc giaToán
Cho hàm số
liên tục trên
có đồ thị như hình vẽ dưới. Gọi
là diện tích hình phẳng giới hạn bởi đồ thị hàm số
, trục hoành và các đường thẳng
Mệnh đề nào sau đây đúng?
Lượt xem: 141,800 Cập nhật lúc: 04:31 17/05/2025
#8223 THPT Quốc giaToán
Cho hàm số
liên tục trên , diện tích của hình phẳng giới hạn bởi đồ thị hàm số , trục hoành và hai đường thẳng được tính theo công thứcLượt xem: 139,944 Cập nhật lúc: 07:32 17/05/2025
#11384 THPT Quốc giaToán
Cho đồ thị hàm số
liên tục trên
và có đồ thị như hình vẽ.
Số nghiệm của phương trình là
Lượt xem: 193,676 Cập nhật lúc: 08:28 17/05/2025
#7949 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn và có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình trên đoạn làLượt xem: 135,242 Cập nhật lúc: 07:32 17/05/2025
#11376 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có đồ thị như hình vẽ bên dưới. Gọi
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
. Ta có
bằng:
Lượt xem: 193,546 Cập nhật lúc: 10:38 17/05/2025
#8358 THPT Quốc giaToán
Cho hàm số
có đạo hàm liên tục trên
và có đồ thị hàm số
như hình vẽ
Có bao nhiêu giá trị nguyên của để hàm số có 3 điểm cực trị dương?
Lượt xem: 142,260 Cập nhật lúc: 04:55 17/05/2025
#8112 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có đồ thị trên đoạn
như hình vẽ bên. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
trên đoạn
bằng
Lượt xem: 138,017 Cập nhật lúc: 07:38 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
5,307 xem398 thi
