Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8631

Cho hàm số y=f(x)y = f \left( x \right) có đồ thị như hình dưới đây. Số nghiệm thực của phương trình 3−f(x)1+f(x)=5\dfrac{3 - f \left( x \right)}{1 + f \left( x \right)} = 5

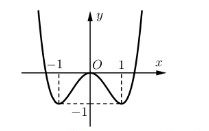
Hình ảnh


A.  

3.

B.  

5.

C.  

2.

D.  

4.

Đáp án đúng là: D

Cho hàm số y=f(x)y = f \left( x \right) có đồ thị như hình dưới đây. Số nghiệm thực của phương trình 3−f(x)1+f(x)=5\dfrac{3 - f \left( x \right)}{1 + f \left( x \right)} = 5



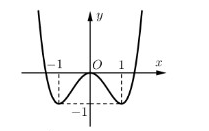
A. 3. B. 5. C. 2. D. 4.
Lời giải
Phương trình đã cho tương đương với f(x)=−13f \left( x \right) = - \dfrac{1}{3}.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f(x)y = f \left( x \right)với đường thẳng y=−13y = - \dfrac{1}{3}. Dựa vào đồ thị ta thấy đường thẳng y=−13y = - \dfrac{1}{3} cắt đồ thị hàm số y=f(x)y = f \left( x \right) tại 4 điểm phân biệt nên phương trình có 4 nghiệm phân biệt.


 

Câu hỏi tương tự:

#8593 THPT Quốc giaToán

Cho hàm số y=ax−bx−1y = \dfrac{a x - b}{x - 1} có đồ thị như hình vẽ bên dưới



Mệnh đề nào dưới đây đúng?

Lượt xem: 146,114 Cập nhật lúc: 16:50 22/11/2024

#7926 THPT Quốc giaToán

Cho hàm số y=ax4+bx2+cy = a x^{4} + b x^{2} + c có đồ thị như hình bên.
OO

−2- 2 −1- 1 11 22
Mệnh đề nào dưới đây đúng?

Lượt xem: 134,810 Cập nhật lúc: 04:16 23/11/2024

#7913 THPT Quốc giaToán

Cho hàm số y=2x3+bx2+cx+dy = 2 x^{3} + b x^{2} + c x + d có đồ thị như hình vẽ. Khẳng định nào dưới đây là đúng

Lượt xem: 134,591 Cập nhật lúc: 03:24 24/11/2024

#8591 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đồ thị f′(x)f^{'} \left( x \right) như hình vẽ



Hàm số g(x)=f(x2)−x63+x4−x2g \left( x \right) = f \left( x^{2} \right) - \dfrac{x^{6}}{3} + x^{4} - x^{2} đồng biến trên khoảng nào dưới đây?

Lượt xem: 146,080 Cập nhật lúc: 11:55 23/11/2024

#7623 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) có đồ thị như hình vẽ sau. Hàm số đã cho đồng biến trên khoảng nào dưới đây?


Lượt xem: 129,622 Cập nhật lúc: 07:14 23/11/2024

#11138 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right)có đồ thị là đường cong như hình vẽ dưới đây.



Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

Lượt xem: 189,367 Cập nhật lúc: 09:37 23/11/2024

#7517 THPT Quốc giaToán

Cho f(x)f \left( x \right) là hàm số đa thức bậc bốn và hàm số y=f′(x)y = f^{'} \left( x \right) có đồ thị là đường cong như hình dưới đây.



Hàm số g(x)=f(sinx−1)+cos2x4g \left( x \right) = f \left( sin x - 1 \right) + \dfrac{cos2 x}{4} có bao nhiêu điểm cực trị thuộc khoảng (0;2π)\left( 0 ; 2 \pi \right)?

Lượt xem: 127,821 Cập nhật lúc: 05:41 23/11/2024

#7907 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) có đồ thị như hình vẽ bên dưới



Hàm số y=f(x)y = f \left( x \right) nghịch biến trên khoảng nào sau đây?

Lượt xem: 134,451 Cập nhật lúc: 04:21 24/11/2024

#8812 THPT Quốc giaToán

Cho hàm số y=ax4+bx2+c(a,b,c∈R)y = a x^{4} + b x^{2} + c \left( a , b , c \in \mathbb{R} \right) có đồ thị là đường cong như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

Lượt xem: 149,846 Cập nhật lúc: 08:10 23/11/2024


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT Nguyễn Khuyến - TPHCM - Lần 1THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

835 lượt xem 413 lượt làm bài