Cho hàm số trùng phương $y = \left(\text{ax}\right)^{4} + b x^{2} + c$ có đồ thị như hình vẽ.

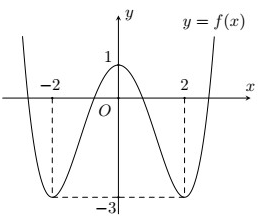
Hỏi đồ thị hàm số $y = \dfrac{\left( x^{2} - 4 \right) \left( x^{2} + 2 x \right)}{\left(\left[\right. f \left( x \right) \left]\right.\right)^{2} + 2 f \left( x \right) - 3}$ có tổng cộng bao nhiêu tiệm cận đứng?

A.  

$3$.

B.  

$4$.

C.  

$5$.

D.  

$2$

Đáp án đúng là: B

Để giải bài toán này, trước tiên chúng ta cần phân tích các thông tin từ hình vẽ và hàm số đã cho.

Hàm số trùng phương có dạng:

$y = ax^4 + bx^2 + c$

Dựa vào đồ thị, chúng ta có thể thấy rằng hàm số có 3 điểm cực trị. Điều này có nghĩa là hệ số  $a$ và  $b$ phải có giá trị sao cho phương trình:

$y' = 4ax^3 + 2bx = 0$

có ba nghiệm phân biệt, điều này dẫn đến:

$b^2 - 4ac > 0$

Do đó, hàm số trùng phương này có 3 điểm cực trị, nghĩa là hệ số  $b$ khác 0.

Tiếp theo, chúng ta xét hàm số cần tìm số lượng tiệm cận đứng:

$y = \dfrac{\left( x^{2} - 4 \right) \left( x^{2} + 2x \right)}{\left(f(x)\right)^{2} + 2f(x) - 3}$

Để tìm các tiệm cận đứng, chúng ta cần xét điều kiện khi mẫu số của hàm số bằng 0, tức là giải phương trình:

$\left(f(x)\right)^{2} + 2f(x) - 3 = 0$

Giải phương trình này theo  $f(x)$, ta có:

$f(x) = \dfrac{-2 \pm \sqrt{4 + 12}}{2} = \dfrac{-2 \pm \sqrt{16}}{2} = \dfrac{-2 \pm 4}{2}$

Như vậy:

$f(x) = 1$ hoặc  $f(x) = -3$

Tiếp theo, ta giải các phương trình:

$ax^4 + bx^2 + c = 1$

và

$ax^4 + bx^2 + c = -3$

Vì hàm số trùng phương có 3 điểm cực trị, nên mỗi phương trình sẽ có tối đa 2 nghiệm (vì bậc của phương trình là 4). Do đó, tổng số nghiệm của cả hai phương trình là 4.

Mỗi nghiệm tương ứng với một tiệm cận đứng của hàm số. Vậy, hàm số có tổng cộng 4 tiệm cận đứng.

Đáp án đúng là:

B:  $4$.