Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8827

Cho hình lăng trụ ABC.A′B′C′A B C . A ' B ' C 'có các mặt bên đều là hình vuông. Gọi M,NM , Nlần lượt là trung điểm của các cạnh BC,​A′C′B C , ​ A ' C '. Biết khoảng cách giữa hai đường thẳng MNM Nvà AB′A B ' bằng a32\dfrac{a \sqrt{3}}{2}. Thể tích khối chóp A′ABCA ' A B C bằng

A.  

23a32 \sqrt{3} a^{3}.

B.  

3a3\sqrt{3} a^{3}.

C.  

23a33\dfrac{2 \sqrt{3} a^{3}}{3}.

D.  

3a33\dfrac{\sqrt{3} a^{3}}{3}.

Đáp án đúng là: C



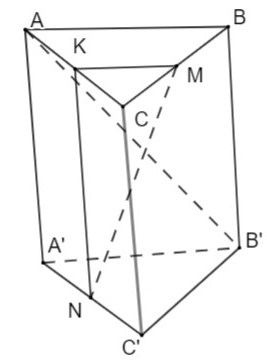
Chọn C
Gọi K trung điểm ACA C, khi đó MK//ABM K / / A B, KN//AA′K N / / A A ' suy ra (KMN)//(ABB′A′)\left( K M N \right) / / \left( A B B ' A ' \right)
Do đó d(MN,AB′)=d((MNK),(ABB′A′))=d(M;(ABB′A′))d \left( M N , A B ' \right) = d \left(\right. \left( M N K \right) , \left( A B B ' A ' \right) \left.\right) = d \left(\right. M ; \left( A B B ' A ' \right) \left.\right)
Lại có d(C;(ABB′A′))=2d(M;(ABB′A′))=a3⇒AB=2ad \left(\right. C ; \left( A B B ' A ' \right) \left.\right) = 2 d \left(\right. M ; \left( A B B ' A ' \right) \left.\right) = a \sqrt{3} \Rightarrow A B = 2 a
Suy ra VA′.ABC=13d(C;(ABB′A′)).SABC=13.a3.124a2=23a33V_{A ' . A B C} = \dfrac{1}{3} d \left(\right. C ; \left( A B B ' A ' \right) \left.\right) . S_{A B C} = \dfrac{1}{3} . a \sqrt{3} . \dfrac{1}{2} 4 a^{2} = \dfrac{2 \sqrt{3} a^{3}}{3}.


 

Câu hỏi tương tự:

#8853 THPT Quốc giaToán

Cho hình lăng trụ ABCD.A′B′C′D′A B C D . A^{'} B^{'} C^{'} D^{'} có đáy ABCDA B C D là hình vuông cạnh a,  AA′⊥(ABCD)a , \textrm{ }\textrm{ } A A^{'} \bot \left( A B C D \right) và AA′=3a.A A^{'} = 3 a . Thể tích của khối lăng trụ đã cho bằng

Lượt xem: 150,581 Cập nhật lúc: 11:47 25/04/2025

#8059 THPT Quốc giaToán

Cho hình lăng trụ ABCA′B′C′A B C A ' B ' C ' có đáy là tam giác ABCA B C vuông cân tại A, AB=aA , \textrm{ } A B = a, biết thể tích của khối lăng trụ ABCA′B′C′A B C A ' B ' C ' là V=4a33V = \dfrac{4 a^{3}}{3}. Tính khoảng cách hh giữa hai đường thẳng ABA B và B′C′B ' C '.

Lượt xem: 137,095 Cập nhật lúc: 16:54 26/04/2025

#7565 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là tam giác ABCA B C vuông cân tại AA, cạnh BC=a2B C = a \sqrt{2}. Góc giữa mặt phẳng (AB′C)\left( A B^{'} C \right) và mặt phẳng (BCC′B′)\left( B C C^{'} B^{'} \right) bằng 60∘60 \circ. Tính thể tích VV của khối đa diện AB′CA′C′A B^{'} C A^{'} C^{'}.

Lượt xem: 128,780 Cập nhật lúc: 11:52 26/04/2025

#8869 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là tam giác vuông cân tại BB, AB=aA B = a và A′B=a3A^{'} B = a \sqrt{3}. Thể tích khối lăng trụ ABC.A′B′C′A B C . A^{'} B^{'} C^{'} là

Lượt xem: 150,934 Cập nhật lúc: 13:36 23/04/2025

#8604 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A ' B ' C ' có đáy ABCA B C vuông tại A,A , AB=a3A B = a \sqrt{3}, AC=AA′=aA C = A A^{'} = a Giá trị sin của góc giữa đường thẳng AC′A C^{'} và mặt phẳng (BCC′B′)\left( B C C ' B ' \right) bằng

Lượt xem: 146,430 Cập nhật lúc: 10:06 26/04/2025

#8941 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy ABC là tam giác vuông tại B với AB=2a,  BC=aA B = 2 a , \textrm{ }\textrm{ } B C = a và AA′=4a.A A^{'} = 4 a . Gọi M là trung điểm của cạnh AB.A B . Khoảng cách giữa hai đường thẳng AB′A B^{'} và CM bằng

Lượt xem: 152,092 Cập nhật lúc: 10:06 26/04/2025

#7923 THPT Quốc giaToán

Cho hình lăng trụ đều có đáy là tam giác đều cạnh bằng aa, cạnh bên bằng 2a2 a. Tính thể tích khối lăng trụ đó.

Lượt xem: 134,858 Cập nhật lúc: 13:59 26/04/2025

#8459 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A ' B ' C ' có đáy ABCA B C là tam giác vuông tại BB, BC=aB C = a, mặt phẳng (A′BC)\left( A ' B C \right) tạo với đáy một góc 30∘30 \circ và tam giác A′BCA ' B C có diện tích bằng a23a^{2} \sqrt{3}. Tính thể tích khối lăng trụ ABC.A′B′C′A B C . A ' B ' C '.

Lượt xem: 143,912 Cập nhật lúc: 10:05 26/04/2025

#8071 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là một tam giác vuông cân tại BB. AB=AA′=2a,A B = A A^{'} = 2 a , M,NM , N lần lượt là trung điểm của BCB Cvà BB′B B^{'}. Khoảng cách giữa hai đường thẳng MNM N và AC′A C^{'} bằng

Lượt xem: 137,290 Cập nhật lúc: 07:28 26/04/2025


Đề thi chứa câu hỏi này:

46. Đề thi thử TN THPT môn Toán năm 2024 - SỞ GIÁO DỤC THÁI NGUYÊN

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,742 xem352 thi