Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8360

Cho hình nón có bán kính đáy bằng 3 chiều cao bằng 6, một khối trụ có bán kính đáy thay đổi nội tiếp khối nón đã cho (như hình vẽ). Khi thể tích khối trụ đạt giá trị lớn nhất thì diện tích toàn phần của hình trụ bằng

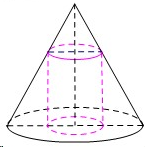
Hình ảnh

A.  

8π8 \pi.

B.  

12π12 \pi.

C.  

16π16 \pi.

D.  

10π10 \pi.

Đáp án đúng là: C



Gọi bán kính của khối trụ là x  (0<x<3)x \textrm{ }\textrm{ } \left( 0 < x < 3 \right), chiều cao của khối trụ là h=OO′ (0<h<6)h = O O^{'} \textrm{ } \left( 0 < h < 6 \right).
Khi đó thể tích khối trụ là: V=πx2hV = \pi x^{2} h.
Ta có: ΔSO′N\Delta S O^{'} N đồng dạng với ΔSOB\Delta S O B nên có O′NOB=SO′SO⇔x3=6−h6⇔h=6−2x\dfrac{O^{'} N}{O B} = \dfrac{S O^{'}}{S O} \Leftrightarrow \dfrac{x}{3} = \dfrac{6 - h}{6} \Leftrightarrow h = 6 - 2 x.
Suy ra V=πx2h=πx2(6−2x)=π(6x2−2x3)V = \pi x^{2} h = \pi x^{2} \left( 6 - 2 x \right) = \pi \left( 6 x^{2} - 2 x^{3} \right).
Xét hàm f(x)=6x2−2x3,   (0<x<3)f \left( x \right) = 6 x^{2} - 2 x^{3} , \textrm{ }\textrm{ }\textrm{ } \left( 0 < x < 3 \right).
f′(x)=12x−6x2f^{'} \left( x \right) = 12 x - 6 x^{2}.
f′(x)=0⇔[x=0  (l)x=2  (n)f^{'} \left( x \right) = 0 \Leftrightarrow \left[ x = 0 \textrm{ }\textrm{ } \left(\right. l \right) \\ x = 2 \textrm{ }\textrm{ } \left( n \right)
Bảng biến thiên:



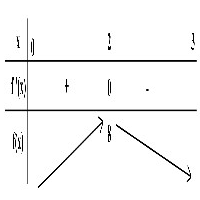
Do đó VV lớn nhất khi hàm f(x)f \left( x \right) đạt giá trị lớn nhất.
Vậy thể tích của khối trụ lớn nhất là V=8πV = 8 \pi khi bán kính khối trụ bằng r=2⇒h=2r = 2 \Rightarrow h = 2
Vậy diện tích toàn phần của hình trụ bằng 2πrh+2πr2=16π.2 \pi r h + 2 \pi r^{2} = 16 \pi .


 

Câu hỏi tương tự:

#8843 THPT Quốc giaToán

Cho hình nón có bán kính đáy bằng 4, chiều cao bằng 8. Một khối trụ có bán kính đáy thay đổi và nội tiếp hình nón đã cho (tham khảo hình vẽ). Thể tích của khối trụ đạt giá trị lớn nhất bằng

Lượt xem: 150,442 Cập nhật lúc: 13:35 20/02/2025

#8750 THPT Quốc giaToán

Cho hình nón có bán kính đáy bằng aa và chiều cao bằng aa. Độ dài đường sinh của hình nón bằng

Lượt xem: 148,808 Cập nhật lúc: 17:13 21/02/2025

#7715 THPT Quốc giaToán

Cho hình nón có bán kính đáy bằng aa và độ dài đường sinh bằng 2a.2 a . Diện tích xung quanh của hình nón đó bằng

Lượt xem: 131,272 Cập nhật lúc: 19:25 22/02/2025

#8852 THPT Quốc giaToán

Cho hình nón có bán kính đáy bằng 3a3 a và đường sinh bằng 5a.5 a . Diện tích xung quanh hình nón đã cho bằng

Lượt xem: 150,532 Cập nhật lúc: 14:25 21/02/2025

#8525 THPT Quốc giaToán

Cho hình nón có bán kính đáy bằng 4a4 a, chiều cao là 3a3 a. Diện tích toàn phần của hình nón bằng

Lượt xem: 145,016 Cập nhật lúc: 17:18 22/02/2025

#8113 THPT Quốc giaToán

Cho khối nón có bán kính đáy bằng 3 cm3 \textrm{ } \text{cm}, góc ở đỉnh hình nón là 60∘60 \circ. Thể tích khối nón bằng

Lượt xem: 137,968 Cập nhật lúc: 04:40 21/02/2025

#8493 THPT Quốc giaToán

Cho hình nón có bán kính đáy là 4r4 r và diện tích xung quanh là SS. Đường sinh của hình nón bằng

Lượt xem: 144,474 Cập nhật lúc: 13:25 22/02/2025

#7559 THPT Quốc giaToán

Cho hình nón có chiều cao bằng 8 cm8 \textrm{ } \text{cm}, bán kính đáy bằng 6 cm6 \textrm{ } \text{cm}. Diện tích toàn phần của hình nón đã cho bằng

Lượt xem: 128,616 Cập nhật lúc: 11:25 21/02/2025

#8326 THPT Quốc giaToán

Cho hình nón tròn xoay có chiều cao bằng 2a2 a, bán kính đáy bằng 3a3 a. Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện bằng 3a2\dfrac{3 a}{2}. Diện tích của thiết diện đó bằng

Lượt xem: 141,590 Cập nhật lúc: 13:59 19/02/2025


Đề thi chứa câu hỏi này:

37 . Đề thi thử TN THPT môn Toán năm 2024 - THPT TRIỆU SƠN 3 - TH.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,870 lượt xem 2,527 lượt làm bài