Cho hình trụ có bán kính đáy bằng
và chiều cao bằng
. Mặt phẳng
song song với trục của hình trụ và cách trục một khoảng bằng
. Diện tích thiết diện của hình trụ cắt bởi mặt phẳng
là
A.
.
B.
.
C.
.
D.
.
Chi tiết
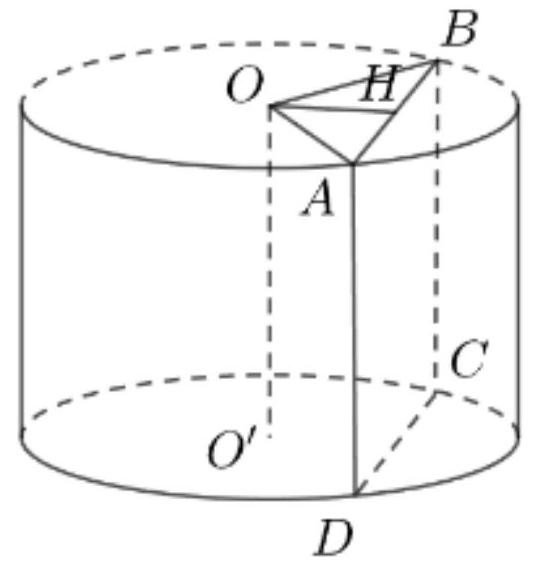
Giả sử
cắt hình trụ theo thiết diện là hình chữ nhật
Gọi
là trung điểm của
. Khi đó
Gọi
lần lượt là tâm của hai mặt đáy
Theo giả thiết ta có
Lại có:
Diện tích thiết diện
là
Chọn D.
Đáp án đúng là: D
Cho hình trụ có bán kính đáy bằng và chiều cao bằng . Mặt phẳng song song với trục của hình trụ và cách trục một khoảng bằng . Diện tích thiết diện của hình trụ cắt bởi mặt phẳng là
.
.
.
.
Chi tiết

Giả sử cắt hình trụ theo thiết diện là hình chữ nhật
Gọi là trung điểm của . Khi đó
Gọi lần lượt là tâm của hai mặt đáy
Theo giả thiết ta có
Lại có:
Diện tích thiết diện là
Chọn D.
Đáp án đúng là: D
Câu hỏi tương tự:
#7631 THPT Quốc giaToán
Cho hình trụ có bán kính đáy và chiều cao . Diện tích toàn phần của hình trụ đã cho bằng
Lượt xem: 129,880 Cập nhật lúc: 04:18 16/05/2025
#8707 THPT Quốc giaToán
Cho hình trụ có chiều cao bằng và bán kính đáy . Diện tích toàn phần của hình trụ đã cho bằng
Lượt xem: 148,161 Cập nhật lúc: 16:53 13/05/2025
#8466 THPT Quốc giaToán
Cho hình trụ có bán kính đáy và diện tích xung quanh là . Chiều cao của hình trụ bằng
Lượt xem: 144,074 Cập nhật lúc: 20:14 13/05/2025
#8843 THPT Quốc giaToán
Cho hình nón có bán kính đáy bằng 4, chiều cao bằng 8. Một khối trụ có bán kính đáy thay đổi và nội tiếp hình nón đã cho (tham khảo hình vẽ). Thể tích của khối trụ đạt giá trị lớn nhất bằng
Lượt xem: 150,494 Cập nhật lúc: 13:13 15/05/2025
#8808 THPT Quốc giaToán
Cho mặt cầu có bán kính bằng 4, hình trụ có chiều cao bằng 4 và hai đường tròn đáy nằm trên . Gọi là thể tích khối trụ và là thể tích của khối cầu . Tỉ số bằng
Lượt xem: 149,904 Cập nhật lúc: 23:06 15/05/2025
#11142 THPT Quốc giaToán
Cho hình trụ có bán kính đáy và độ dài đường sinh . Diện tích xung quanh của hình trụ đã cho bằng
Lượt xem: 189,493 Cập nhật lúc: 16:46 13/05/2025
#8426 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , thiết diện qua trục của hình trụ là hình vuông. Gọi và là hai điểm lần lượt nằm trên hai đường tròn và . Biết và khoảng cách giữa và bằng . Bán kính đáy của hình trụ bằng
Lượt xem: 143,354 Cập nhật lúc: 20:19 17/05/2025
#8740 THPT Quốc giaToán
Cho hình trụ có tâm hai đường tròn đáy lần lượt là và , bán kính đáy hình trụ bằng . Trên đường tròn đáy và lần lượt lấy hai điểm sao cho tạo với trục của hình trụ một góc và có khoảng cách đến trục của hình trụ bằng . Tính thể tíc khối chóp
Lượt xem: 148,662 Cập nhật lúc: 12:00 17/05/2025
#8204 THPT Quốc giaToán
Cho hình trụ có diện tích xung quanh bằng và độ dài đường sinh bằng đường kính của đường tròn đáy. Bán kính của đường tròn đáy là
Lượt xem: 139,627 Cập nhật lúc: 07:05 13/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
4,924 xem371 thi
