Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8808

Cho mặt cầu (S)\left( S \right) có bán kính bằng 4, hình trụ (H)\left( H \right) có chiều cao bằng 4 và hai đường tròn đáy nằm trên (S)\left( S \right). Gọi V1V_{1} là thể tích khối trụ (H)\left( H \right) và V2V_{2} là thể tích của khối cầu (S)\left( S \right). Tỉ số V1V2\dfrac{V_{1}}{V_{2}} bằng

A.  

916.\dfrac{9}{16} .

B.  

316.\dfrac{3}{16} ..

C.  

23.\dfrac{2}{3} .

D.  

13.\dfrac{1}{3} .

Đáp án đúng là: A

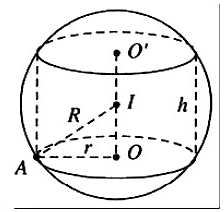
Bán kính đáy hình trụ r=R2−(h2)2r = \sqrt{R^{2} - \left( \dfrac{h}{2} \right)^{2}}


Cách giải:
V2=43π.43V_{2} = \dfrac{4}{3} \pi . 4^{3}
r2=42−22=23r_{2} = \sqrt{4^{2} - 2^{2}} = 2 \sqrt{3}
⇒V1=4.π(23())2⇒V1V2=23\Rightarrow V_{1} = 4 . \pi \left( 2 \sqrt{3} \left(\right)\right)^{2} \Rightarrow \dfrac{V_{1}}{V_{2}} = \dfrac{2}{3}


 

Câu hỏi tương tự:

#8838 THPT Quốc giaToán

Trong không gian Oxyz,O x y z , cho mặt cầu (S):x2+y2+(z−2)2=16.\left( S \right) : x^{2} + y^{2} + \left( z - 2 \right)^{2} = 16 . Mặt phẳng (Oxy)\left( O x y \right) cắt (S)\left( S \right) theo giao tuyến là một đường tròn có bán kính bằng

Lượt xem: 150,288 Cập nhật lúc: 21:44 11/01/2025

#7725 THPT Quốc giaToán

Trong không gian với hệ toạ độ OxyzO x y z, cho mặt phẳng (P):x+y+z=0\left( P \right) : x + y + z = 0và mặt cầu (S)\left( S \right) có tâm I(0;1;2)I \left( 0 ; 1 ; 2 \right) bán kính R=1R = 1. Xét điểm MM thay đổi trên (P)\left( P \right). Khối nón có đỉnh II và đường tròn đáy là đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ MM đến (S)\left( S \right). Khi (N)\left( N \right) có thể tích lớn nhất, mặt phẳng chứa đường tròn đáy của (N)\left( N \right) có phương trình là x+ay+bz+c=0x + a y + b z + c = 0. Giá trị của a+b+ca + b + c bằng

Lượt xem: 131,372 Cập nhật lúc: 18:36 18/01/2025

#8346 THPT Quốc giaToán

Cho một hình trụ có chiều cao hh, bán kính đáy R=2hR = 2 h. Biết diện tích xung quanh của hình trụ đó bằng diện tích của một mặt cầu có bán kính aa. Tính diện tích toàn phần của hình trụ.

Lượt xem: 141,982 Cập nhật lúc: 14:09 16/01/2025

#8605 THPT Quốc giaToán

Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S)\left( S \right) có tâm thuộc mặt phẳng (P):x+2y+z−7=0\left( P \right) : x + 2 y + z - 7 = 0 và đi qua hai điểm A(1;2;1),  B(2;5;3)A \left( 1 ; 2 ; 1 \right) , \textrm{ }\textrm{ } B \left( 2 ; 5 ; 3 \right). Bán kính nhỏ nhất của mặt cầu (S)\left( S \right) bằng:

Lượt xem: 146,414 Cập nhật lúc: 12:56 18/01/2025

#11183 THPT Quốc giaToán

Cho hai mặt cầu (S1)\left( S_{1} \right) và (S2)\left( S_{2} \right) đồng tâm II, có bán kính lần lượt là R1=2R_{1} = 2 và R2=10R_{2} = \sqrt{10}. Xét tứ diện ABCDA B C D có hai đỉnh A, BA , \textrm{ } B nằm trên (S1)\left( S_{1} \right) và hai đỉnh C, DC , \textrm{ } D nằm trên (S2)\left( S_{2} \right). Thể tích lớn nhất của khối tứ diện ABCDA B C D bằng

Lượt xem: 190,143 Cập nhật lúc: 20:43 15/01/2025

#8810 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có góc giữa mặt phẳng chứa mặt bên và mặt phẳng đáy bằng 60∘60 \circ. Biết rằng mặt cầu ngoại tiếp hình chóp S.ABCDS . A B C D có bán kính R=3.R = \sqrt{3} . Tính thể tích của khối chóp S.ABCS . A B C.

Lượt xem: 149,807 Cập nhật lúc: 16:59 10/01/2025

#11395 THPT Quốc giaToán

Cho hai mặt phẳng (P)\left( P \right)và (Q)\left( Q \right) song song với nhau và cùng cắt khối cầu tâm OO bán kính 434 \sqrt{3} thành hai hình tròn có cùng bán kính. Xét hình nón có đỉnh trùng với tâm của một trong hai hình tròn này và có đáy là hình tròn còn lại. Khi diện tích xung quanh của hình nón là lớn nhất, khoảng cách hh giữa hai mặt phẳng (P)\left( P \right)và (Q)\left( Q \right) bằng:

Lượt xem: 193,746 Cập nhật lúc: 10:21 18/01/2025

#11408 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có AB=4a,BC=32a,A B = 4 a , B C = 3 \sqrt{2} a , ABC^=45∘;SAC^=SBC^=90∘\hat{A B C} = 45 \circ ; \hat{S A C} = \hat{S B C} = 90 \circ; Sin góc giữa hai mặt phẳng (SAB)\left( S A B \right)và (SBC)\left( S B C \right) bằng 24.\dfrac{\sqrt{2}}{4} . Bán kính mặt cầu ngoại tiếp hình chóp đã cho bằng

Lượt xem: 193,994 Cập nhật lúc: 11:11 18/01/2025

#8278 THPT Quốc giaToán

Trong không gian OxyzO x y z, cho mặt cầu (S)\left( S \right) có tâm I(0;−2;1)I \left( 0 ; - 2 ; 1 \right) và bán kính R=5R = 5. Phương trình của (S)\left( S \right) là

Lượt xem: 140,805 Cập nhật lúc: 11:00 18/01/2025


Đề thi chứa câu hỏi này:

54. Đề thi thử TN THPT môn Toán năm 2024 - THPT Triệu Sơn 5 - Thanh HóaTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,603 lượt xem 2,408 lượt làm bài