Một viên gạch hoa hình vuông cạnh
. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa.
Diện tích mỗi cánh hoa của viên gạch bằng
với
,
,
và
nguyên tố cùng nhau. Tính
.
A. 250.
B. 403.
C. 800.
D. 803.
Đáp án đúng là: B
Một viên gạch hoa hình vuông cạnh
. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa.

Diện tích mỗi cánh hoa của viên gạch bằng với , , và nguyên tố cùng nhau. Tính .
250.
403.
800.
803.
Đáp án đúng là: B
Chọn hệ trục toạ độ
như hình vẽ.
Với
, xét hình phẳng ở góc phần tư thứ nhất, hai parabol có phương trình lần lượt là
và
.
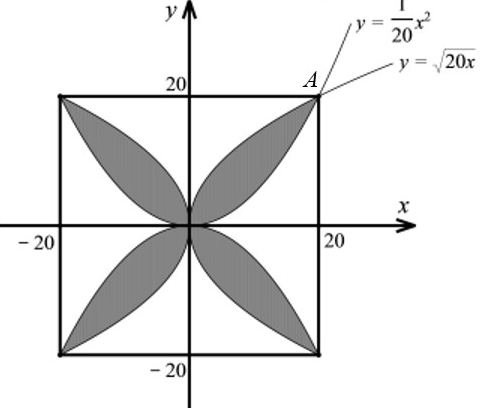
Do đi qua nên Phương trình .
Do đi qua nên Phương trình .
Diện tích cánh hoa ở góc phần tư thứ nhất là: .
Do đó: . Vậy .
Câu hỏi tương tự:
#8427 THPT Quốc giaToán
Một số viên gạch hình hộp chữ nhật như nhau được xếp thành một chồng gạch dạng hình lập phương có cạnh bằng
. Thể tích của mỗi viên gạch bằng
Lượt xem: 143,386 Cập nhật lúc: 09:15 27/04/2025
#2960 THPT Quốc giaVật lý
Một con lắc lò xo gồm một lò xo khối lượng không đáng kể, độ cứng k, một đầu cố định và một đầu gắn với một viên bi nhỏ khối lượng m. Con lắc này đang dao động điều hòa có cơ năng
Lượt xem: 50,470 Cập nhật lúc: 18:55 27/04/2025
#8762 THPT Quốc giaToán
Có ba chiếc hộp: hộp I có 4 bi đỏ và 5 bi xanh, hộp II có 3 bi đỏ và 2 bi đen, hộp III có 5 bi đỏ và 3 bi vàng. Lấy ngẫu nhiên ra một hộp rồi lấy một viên bi từ hộp đó. Xác suất để viên bi lấy được màu đỏ bằng
Lượt xem: 149,030 Cập nhật lúc: 12:14 26/04/2025
#7332 THPT Quốc giaVật lý
Một lò xo có độ cứng một đầu treo cố định, đầu còn lại gắn viên bi có khối lượng tạo thành con lắc lò xo treo thẳng đứng. Người ta tác dụng vào viên bi một ngoại lực (chi có f thay đổi được) làm cho viên bi dao động dọc theo trục của lò xo. Khi cho f thay đổi thì biên độ dao động của viên bi thay đổi, khi thì biên độ của viên bi lớn nhất. Cho . Khối lượng của viên bi bằng
Lượt xem: 124,868 Cập nhật lúc: 19:14 27/04/2025
#11409 THPT Quốc giaToán
Một hộp có 6 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ ba màu và số viên bi đỏ lớn hơn số viên bi vàng.
Lượt xem: 194,069 Cập nhật lúc: 14:05 27/04/2025
#6809 THPT Quốc giaVật lý
Một con lắc lò xo gồm viên bi nhỏ và lò xo nhẹ có độ cứng , dao động điều hòa với biên độ . Mốc thế năng ở vị trí cân bằng. Khi viên bi cách vị trí cân bằng thì động năng của con lắc bằng
Lượt xem: 115,842 Cập nhật lúc: 06:06 27/04/2025
#8500 THPT Quốc giaToán
Từ một hộp chứa 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng; lấy ngẫu nhiên đồng thời 2viên bi. Xác suất để lấy được 2 viên bi khác màu bằng
Lượt xem: 144,598 Cập nhật lúc: 10:10 26/04/2025
#7100 THPT Quốc giaVật lý
Một lò xo được gắn với một pít-tông P nằm ngang như hình vẽ. Viên bi nhỏ M được gắn cố định trên bánh xe và quay đều quanh trục với tốc độ 1 m/s. Trong quá trình viên bi chuyển động tròn đều thì khoảng cách lớn nhất, nhỏ nhất giữa viên bi và pít-tông lần lượt là 26 cm và 24 cm. Khi khoảng cách giữa viên bi và pít-tông lớn nhất thì lò xo dãn 4 cm. Khoảng thời gian lò xo bị nén khi viên bi quay được một vòng là
Lượt xem: 120,775 Cập nhật lúc: 08:39 27/04/2025
#8632 THPT Quốc giaToán
Ông A bị nhiễm một loại virus nên phải nhập viện và được điều trị ngay lập tức. Kể từ ngày nhập viện, sau mỗi ngày điều trị thì lượng virus trong cơ thể ông A giảm đi so với ngày trước đó. Hỏi sau ít nhất bao nhiêu ngày thì ông A sẽ được xuất viện, biết rằng ông A được xuất viện khi lượng virus trong cơ thể không quá so với ngày nhập viện
Lượt xem: 146,950 Cập nhật lúc: 06:08 27/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
4,303 xem316 thi
