Một vật dao động điều hoà với phương trình
. Trên vật gắn với một nguồn sáng phát ánh sáng đơn sắc có tần số 5.1014 Hz , công suất 0,53W. Biết hằng số Plăng là h = 6,625.10-34 J.s . Tính từ thời điểm t = 0 đến thời điểm gần nhất vật có li độ −3cm thì nguồn sáng phát số phôtôn gần nhất với giá trị nào sau đây?
A. 4.1017 hạt.
B. 8.1017 hạt.
C. 5.1018 hạt.
D. 1,6.1018 hạt.
Đáp án đúng là: A
Một vật dao động điều hoà với phương trình . Trên vật gắn với một nguồn sáng phát ánh sáng đơn sắc có tần số 5.1014 Hz , công suất 0,53W. Biết hằng số Plăng là h = 6,625.10-34 J.s . Tính từ thời điểm t = 0 đến thời điểm gần nhất vật có li độ −3cm thì nguồn sáng phát số phôtôn gần nhất với giá trị nào sau đây?
4.1017 hạt.
8.1017 hạt.
5.1018 hạt.
1,6.1018 hạt.
Đáp án đúng là: A
Số photon nguồn sáng phát ra:
với P là công suất nguồn phát, Δt là thời gian.
Sử dụng VTLG tính được Δt.
Giải chi tiết:
Chu kì:
Lúc t=0 ứng với pha ban đầu
Thời điểm gần nhất vật có li độ
(vị trí M0).
Biểu diễn trên VTLG ta có:
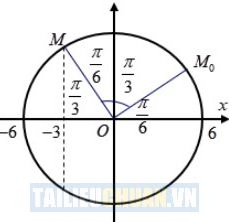
Góc quét được:
⇒ Khoảng thời gian vật đi được:
Số phôtôn gần nhất mà nguồn sáng phát ra là:
(hạt)
Câu hỏi tương tự:
#5836 THPT Quốc giaVật lý
Một vật dao động điều hòa trên trục với phương trình tính bằng s). Tần số góc của dao động này bằng
Lượt xem: 99,310 Cập nhật lúc: 10:31 14/05/2025
#4159 THPT Quốc giaVật lý
Một vật dao động điều hòa trên trục với phương trình , quãng đường vật đi được từ thời điểm ban đầu đến thời điểm là:
Lượt xem: 70,892 Cập nhật lúc: 05:10 15/05/2025
#1914 THPT Quốc giaVật lý
Một vật dao động điều hòa trên trục Ox với phương trình . Tại thời điểm , vật có li độ , vận tốc . Tại thời điểm , vật có li độ , vận tốc . Nhận xét nào sau đây là sai?
Lượt xem: 32,625 Cập nhật lúc: 15:14 14/05/2025
#221 THPT Quốc giaVật lý
Một vật nhỏ dao động điều hòa trên trục với phương trình . Trong giây đầu tiên kể từ , vật đi được quãng đường . Trong giây thứ 2018 vật đi được quãng đường là
Lượt xem: 3,854 Cập nhật lúc: 02:03 17/05/2025
#11777 THPT Quốc giaVật lý
Một vật dao động điều hòa trên trục Ox theo phương trình
thì quãng đườngchuyển động của vật lần lượt là S1=5cm, S2=15cm và S3. Quãng đường S3 gần nhất với kết quả nào sau đây?
Lượt xem: 200,494 Cập nhật lúc: 22:43 13/05/2025
#100 THPT Quốc giaVật lý
Hai con lắc lò xo giống nhau gồm lò xo nhẹ và vật nặng có khối lượng dao động điều hòa với phương trình lần lượt là và trên hai trục tọa độ song song cùng chiều gần nhau cùng gốc tọa độ. Biết trong quá trình dao động, khoảng cách giữa hai vật lớn nhất bằng 10cm và vận tốc tương đối giữa chúng có độ lớn cực đại bằng 1m/s. Để hai con lắc trên dừng lại thì phải thực hiện lên hệ hai con lắc một công cơ học có độ lớn bằng
Lượt xem: 1,911 Cập nhật lúc: 06:16 14/05/2025
#905 THPT Quốc giaVật lý
16Một con lắc lò xo có vật nhỏ khối lượng dao động điều hòa trên trục với phương trình . Đồ thị biểu diễn động năng theo bình phương li độ như hình vẽ. Lấy Tốc độ trung bình của vật trong một chu kì là
Lượt xem: 15,569 Cập nhật lúc: 22:52 13/05/2025
#6419 THPT Quốc giaVật lý
Một con lắc lò xo dao động điều hòa trên trục với phương trình dao động . Gọi , lần lượt là động năng, thế năng của con lắc. Trong một chu kì là . Thời điểm vận tốc v và li độ x của vật thỏa mãn lần thứ 2016 kể từ thời điểm ban đầu có giá trị gần nhất với giá trị nào sau đây
Lượt xem: 109,312 Cập nhật lúc: 09:31 14/05/2025
#313 THPT Quốc giaVật lý
Một vật nhỏ khối lượng , gắn trên một lò xo nhẹ thẳng đứng có độ cứng , đầu dưới của lò xo gắn cố định. Khi đang nằm cân bằng một vật nhỏ có khối lượng m rơi tự do từ độ cao (so với vị trí cân bằng của xuống va chạm mềm với . Sau va chạm hai vật dính vào nhau và cùng dao động điều hoà theo phương thẳng đứng trùng với trục của lò xo. Lấy gia tốc trọng trường . Để không tách rời trong suốt quá trình dao động thì điều kiện của h không vượt quá
Lượt xem: 5,449 Cập nhật lúc: 21:21 14/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 10 câu hỏi 40 phút
10,013 xem744 thi
