80 câu trắc nghiệm: Thể tích khối đa diện có đáp án

Chương 1: Khối đa diện
Bài 3: Khái niệm về thể tích của khối đa diện
Lớp 12;Toán

Thời gian làm bài: 1 giờ

Chọn mã đề:

Bạn chưa làm Đề số 2!!!

Hãy bắt đầu chinh phục nào!

Xem trước nội dung:

Câu 1: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng

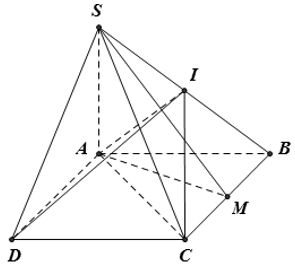
Hình ảnh

\frac{a^{3} \sqrt{6}}{4}

\frac{a^{3} \sqrt{3}}{8}

\frac{a^{3} \sqrt{3}}{2}

\frac{a^{3} \sqrt{3}}{6}

Câu 2: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB=BC= 1 2 AD=a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ACD.

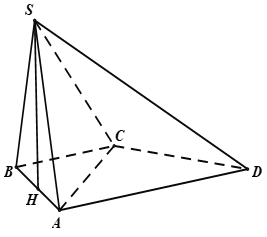
Hình ảnh

V = \frac{a^{3}}{3}

V = \frac{a^{3}}{2}

V = \frac{a^{3} \sqrt{2}}{6}

V = \frac{a^{3} \sqrt{3}}{6}

Câu 3: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có BC = a. Mặt bên SAC vuông góc với đáy các mặt bên còn lại đều tạo với mặt đáy một góc 45°. Thể tích khối chóp S.ABC bằng

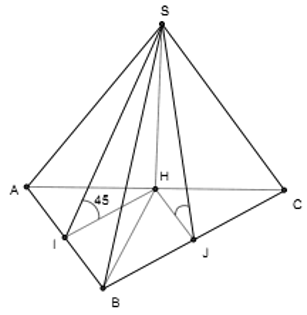
Hình ảnh

\frac{a^{3}}{4}

\frac{a^{3}}{12}

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{4}

Câu 4: 1 điểm

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), S A B ^ = 30°, SA = 2a. Tính thể tích V của khối chóp S.ABCD.

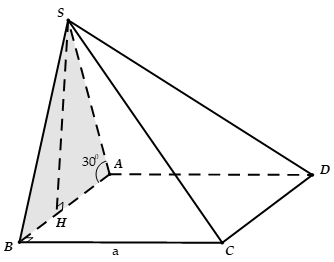
Hình ảnh

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3}}{3}

\frac{a^{3}}{9}

a^{3}

Câu 5: 1 điểm

Cho tứ diện ABCD có ABC là tam giác đều cạnh a tam giác BCD cân tại D và nằm trong mặt phẳng vuông góc với (ABC). Biết AD hợp với mặt phẳng (ABC) một góc 60°. Tính thể tích V của khối tứ diện ABCD.

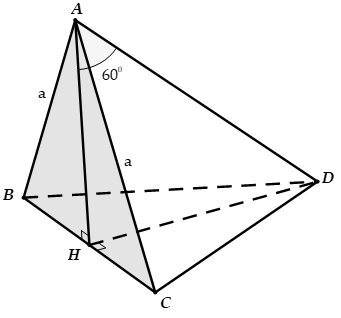
Hình ảnh

V = \frac{a^{3} \sqrt{3}}{6}

V = \frac{a^{3}}{12}

V = \frac{a^{3} \sqrt{3}}{8}

V = \frac{a^{3} \sqrt{3}}{24}

Câu 6: 1 điểm

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), S A B ^ = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD

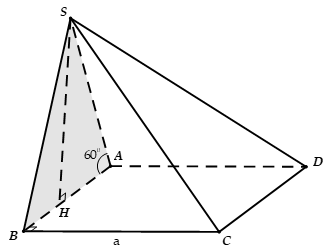
Hình ảnh

V = \frac{a^{3} \sqrt{3}}{3}

V = \frac{a^{3}}{3}

V = \frac{2 a^{3} \sqrt{3}}{3}

V = a^{3}

Câu 7: 1 điểm

Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, BC = 2AB = 2a tam giác SAC nằm trong mặt phẳng vuông góc với (ABCD), S A C ^ = 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD

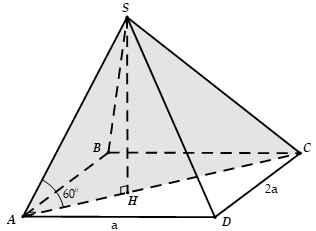
Hình ảnh

V = \frac{a^{3} \sqrt{3}}{3}

V = \frac{a^{3}}{3}

V = \frac{2 a^{3} \sqrt{3}}{3}

V = a^{3}

Câu 8: 1 điểm

Cho hình chóp S.ABCD có đáy là hình vuông tâm O, AB = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm đoạn OA. Góc giữa mặt phẳng (SCD) và mặt phẳng (ABCD) bằng 60°. Tính thể tích V của hình chóp S.ABCD

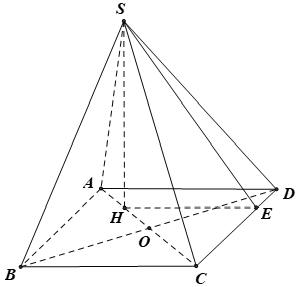
Hình ảnh

V = \frac{3 a^{3} \sqrt{3}}{4}

V = \frac{a^{3} \sqrt{3}}{8}

V = \frac{a^{3} \sqrt{3}}{4}

V = \frac{a^{3} \sqrt{3}}{12}

Câu 9: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 1, góc A B C ^ = 60°, cạnh bên SD = 2 . Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn BD sao cho HD = 3HB. Tính thể tích khối chóp S.ABCD.

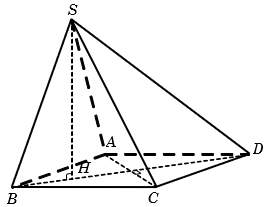
Hình ảnh

V = \frac{\sqrt{5}}{24}

V = \frac{\sqrt{15}}{24}

V = \frac{\sqrt{15}}{8}

V = \frac{\sqrt{15}}{12}

Câu 10: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

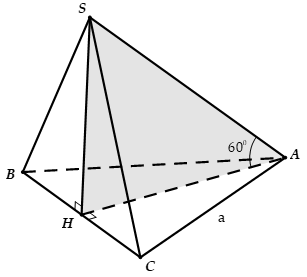
Hình ảnh

V = \frac{a^{3} \sqrt{3}}{8}

B. $V = \frac{a^{3} \sqrt{3}}{24}$

V = \frac{a^{3} \sqrt{5}}{8}

V = \frac{a^{3} \sqrt{3}}{12}

Câu 11: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và (SAB) hợp với đáy một góc 45°. Tính thể tích V của khối chóp S.ABC

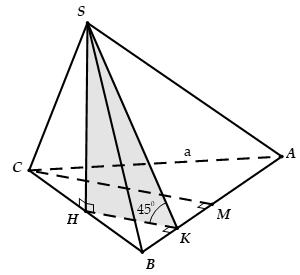
Hình ảnh

V = \frac{3 a^{3}}{16}

B. $V = \frac{a^{3}}{16}$

C. $V = \frac{a^{3}}{8}$

D. $V = \frac{a^{3} \sqrt{3}}{12}$

Câu 12: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, A B C ^ = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.

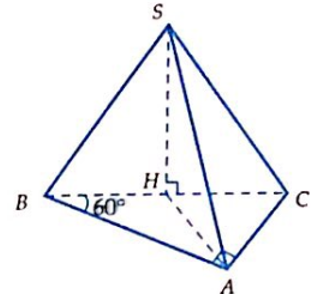
Hình ảnh

4 \sqrt{3}

2 \sqrt{3}

\frac{4}{\sqrt{3}}

Câu 13: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình vuông, BD = 2a, mặt (SAC) là tam giác vuông tại S và nằm trong mặt phẳng vuông góc với đáy, SC = a 3 . Tính thể tích khối chóp S.ABCD.

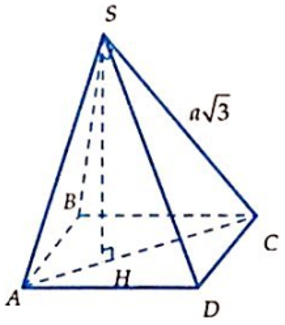
Hình ảnh

\frac{a^{3} \sqrt{3}}{3}

\frac{a^{3} \sqrt{3}}{4}

\frac{2 a^{3} \sqrt{3}}{3}

\frac{a^{3} \sqrt{3}}{6}

Câu 14: 1 điểm

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B; AB = a, BC = a 2 ; mặt phẳng (A'BC) hợp với mặt đáy (ABC) góc 30°. Thể tích của khối lăng trụ là:

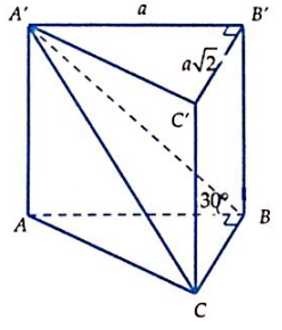
Hình ảnh

a^{3} \sqrt{6}

\frac{a^{3} \sqrt{6}}{12}

C. $\frac{a^{3} \sqrt{6}}{3}$

D. $\frac{a^{3} \sqrt{6}}{6}$

Câu 15: 1 điểm

Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm của AD; M là trung điểm CD; cạnh bên SB hợp với đáy góc 60°. Thể tích của khối chóp S.ABM là:

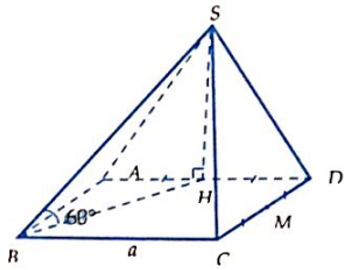
Hình ảnh

\frac{a^{3} \sqrt{15}}{3}

\frac{a^{3} \sqrt{15}}{4}

\frac{a^{3} \sqrt{15}}{6}

\frac{a^{3} \sqrt{15}}{12}

Câu 16: 1 điểm

Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, B A C ^ = 120°, biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC.

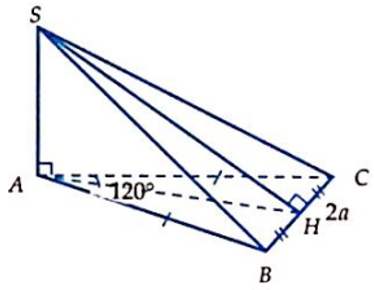
Hình ảnh

V = \frac{a^{3}}{3}

V = \frac{a^{3}}{9}

V = a^{3} \sqrt{2}

V = \frac{a^{3}}{2}

Câu 17: 1 điểm

Một lăng trụ tam giác ABC.A'B'C' có đáy là tam giác đều ABC cạnh a. Cạnh bên bằng b và hợp với mặt đáy góc 60°. Thể tích hình chóp A'.BCC'B' bằng bao nhiêu?

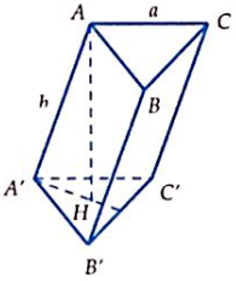
Hình ảnh

\frac{a^{2} b}{4 \sqrt{3}}

\frac{a^{2} b}{4}

\frac{a^{2} b}{2}

\frac{a^{2} b \sqrt{3}}{2}

Câu 18: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho C H → = 2 H B → , SB hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

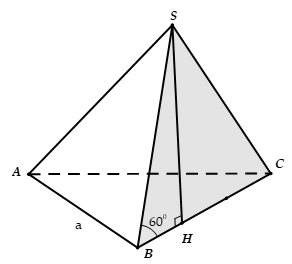
Hình ảnh

V = \frac{a^{3}}{12}

V = \frac{a^{3}}{6}

V = \frac{a^{3}}{4}

V = \frac{a^{3} \sqrt{3}}{12}

Câu 19: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho H C → = 2 B H → , SA hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

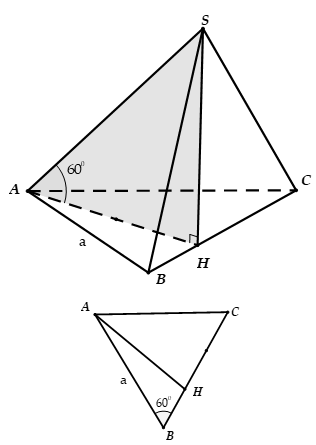
Hình ảnh

V = \frac{a^{3}}{12}

V = \frac{a^{3} \sqrt{7}}{12}

V = \frac{a^{3}}{4}

V = \frac{a^{3} \sqrt{3}}{8}

Câu 20: 1 điểm

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho H C → = 2 B H → , (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

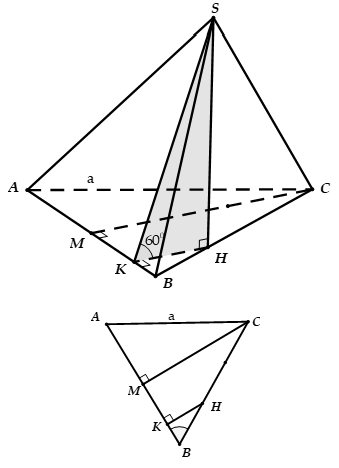
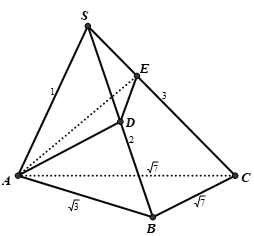
Hình ảnh

V = \frac{a^{3} \sqrt{3}}{24}

V = \frac{a^{3} \sqrt{3}}{12}

V = \frac{a^{3} \sqrt{3}}{4}

V = \frac{a^{3} \sqrt{3}}{6}

Câu 21: 1 điểm

Cho hình chóp S.ABC có các cạnh SA = 1, SB = 2, SC = 3, AB = 3 , BC = CA = 7 . Tính thể tích V khối chóp S.ABC.

Hình ảnh

V = \frac{\sqrt{2}}{4}

V = \frac{\sqrt{3}}{2}

V = \frac{\sqrt{2}}{2}

V = \frac{\sqrt{3}}{4}

Câu 22: 1 điểm

Thể tích khối lăng trụ tam giác đều có cạnh đáy bằng a và cạnh bên bằng 2a là:

\frac{a^{3} \sqrt{2}}{3}

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{2}

\frac{a^{3} \sqrt{3}}{4}

Câu 23: 1 điểm

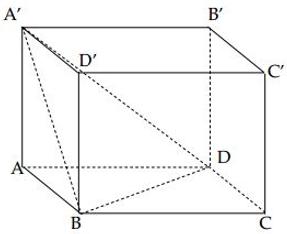
Gọi V là thể tích của hình lập phương ABCD.A'B'C'D'. V 1 là thể tích của tứ diện A'ABD. Hệ thức nào sau đây là đúng?

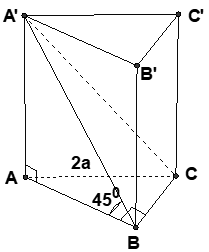
Hình ảnh

V = 6 $V_{1}$

V = 4 $V_{1}$

V = 3 $V_{1}$

V = 2

V_{1}

Câu 24: 1 điểm

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC = 2a biết rằng (A'BC) hợp với đáy (ABC) một góc 45°. Thể tích lăng trụ là:

Hình ảnh

\frac{a^{3} \sqrt{2}}{2}

\frac{a^{3} \sqrt{3}}{3}

a^{3} \sqrt{3}

a^{3} \sqrt{2}

Câu 25: 1 điểm

Cho khối lăng trụ tam giác đều ABC. A 1 B 1 C 1 có tất cả các cạnh bằng a. Gọi M là trung điểm của AA 1 . Thể tích khối chóp M.BC A 1 là:

\frac{a^{3} \sqrt{3}}{12}

\frac{a^{3} \sqrt{3}}{24}

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{8}

Câu 26: 1 điểm

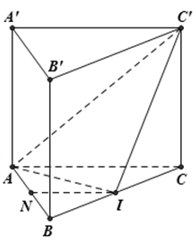
Cho lăng trụ tam giác đều ABC.A’B’C’, cạnh đáy bằng a. Gọi N, I lần lượt là trung điểm của AB, BC; góc giữa hai mặt phẳng (C’AI) và (ABC) bằng 60°. Tính theo a thể tích khối chóp NAC’I?

Hình ảnh

32 a^{3} \sqrt{3}

\frac{a^{3}}{32}

\frac{a^{3} \sqrt{3}}{32}

\frac{a^{3} \sqrt{3}}{4}

Câu 27: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a và (A’BC) hợp với mặt đáy (ABC) một góc 30°. Tính thể tích hình chóp A’.ABC là

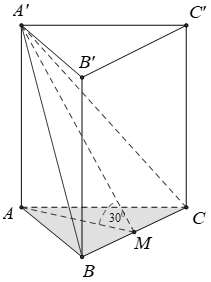
Hình ảnh

\frac{a^{3} \sqrt{3}}{12}

\frac{a^{3} \sqrt{3}}{24}

\frac{3 a^{3}}{24}

\frac{a^{3} \sqrt{5}}{24}

Câu 28: 1 điểm

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (AB’C’) tạo với mặt đáy góc 60°. Tính theo a thể tích lăng trụ ABC.A’B’C’.

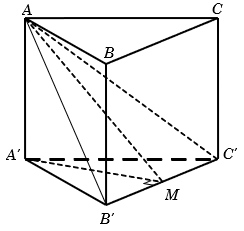
Hình ảnh

\frac{a^{3} \sqrt{3}}{2}

\frac{3 a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{8}

\frac{3 a^{3} \sqrt{3}}{8}

Câu 29: 1 điểm

Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 3a, BC = a 2 , mặt bên (A’BC) hợp với mặt đáy (ABC) một góc 60°. Tính thể tích khối lăng trụ.

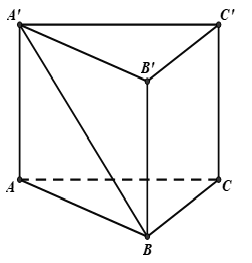
Hình ảnh

\frac{7 a^{3} \sqrt{6}}{2}

\frac{a^{3} \sqrt{6}}{2}

\frac{9 a^{3} \sqrt{6}}{2}

\frac{a^{3} \sqrt{6}}{6}

Câu 30: 1 điểm

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a, ACB ^ = 60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a.

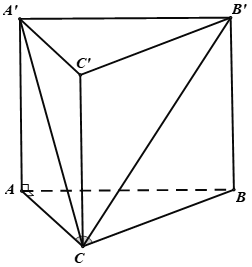
Hình ảnh

\frac{a^{3} \sqrt{15}}{3}

a^{3} \sqrt{6}

\frac{a^{3} \sqrt{15}}{12}

\frac{a^{3} \sqrt{15}}{24}

Câu 31: 1 điểm

Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a; BC = 2a; AA’= a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Tính thể tích khối chóp M.AB’C.

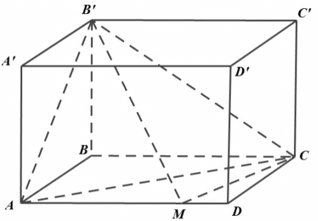
Hình ảnh

V = \frac{a^{3}}{2}

V = \frac{a^{3}}{4}

C. $V = \frac{3 a^{3}}{4}$

D. $V = \frac{3 a^{3}}{2}$

Câu 32: 1 điểm

Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A’BCD’) bằng a 3 2 . Tính thể tích hình hộp theo a.

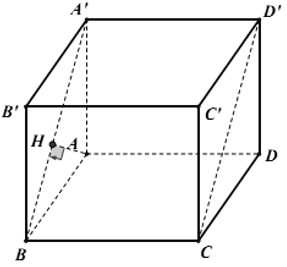
Hình ảnh

a^{3}

\frac{a^{3} \sqrt{21}}{7}

a^{3} \sqrt{3}

D. $\frac{a^{3} \sqrt{3}}{3}$

Câu 33: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, D ^ = 60° và SA vuông góc với (ABCD). Biết thể tích của khối chóp S.ABCD bằng a 3 2 . Tính khoảng cách (k) từ A đến mặt phẳng (SBC).

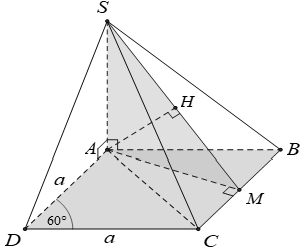
Hình ảnh

k = \frac{3 a}{\sqrt{5}}

k = a \sqrt{\frac{3}{5}}

k = \frac{2 a}{\sqrt{5}}

k = \frac{2 a}{\sqrt{5}}

Câu 34: 1 điểm

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Mặt bên ABB’A’ có diện tích bằng a 2 3 . Gọi M; N lần lượt là trung điểm của A’B; A’C . Tính tỉ số thể tích của hai khối chóp A’. AMN và A’.ABC.

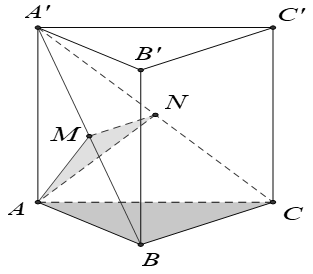
Hình ảnh

\frac{1}{2}

\frac{1}{3}

\frac{1}{4}

\frac{1}{5}

Câu 35: 1 điểm

Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích khối lăng trụ bằng:

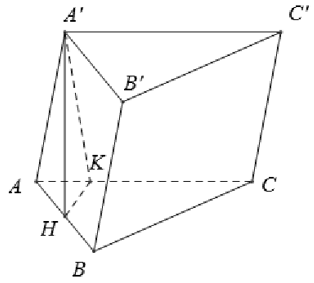
Hình ảnh

V = \frac{3 a^{3}}{32}

V = \frac{3 a^{3}}{16}

V = \frac{3 a^{3}}{4}

V = \frac{3 a^{3}}{8}

Câu 36: 1 điểm

Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a 3 ; BC = 3a, A C B ^ = 30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng:

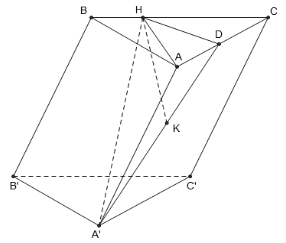
Hình ảnh

\frac{4 a^{3}}{9}

\frac{19 a^{3}}{4}

\frac{9 a^{3}}{4}

\frac{4 a^{3}}{19}

Câu 37: 1 điểm

Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích của khối lăng trụ ABC.A’B’C’ bằng:

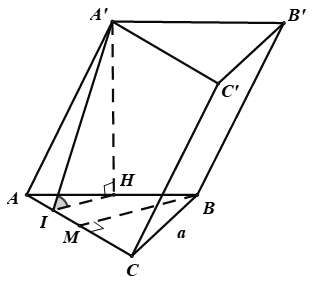
Hình ảnh

\frac{a^{3}}{2}

\frac{3 a^{3}}{4}

\frac{3 a^{3}}{16}

\frac{3 a^{3}}{2}

Câu 38: 1 điểm

Cho lăng trụ tam giác ABC.A’B’C’ đáy ABC là tam giác đều cạnh a, hình chiếu vuông góc H của A’ trên mặt phẳng (ABC) trùng với trực tâm của tam giác ABC. Tất cả các cạnh bên đều tạo với mặt phẳng đáy góc 60°. Thể tích của khối lăng trụ ABC.A’B’C’là:

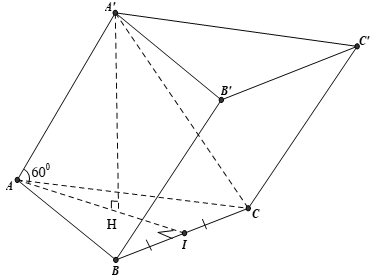
Hình ảnh

\frac{a^{3} \sqrt{3}}{4}

\frac{a^{3} \sqrt{3}}{6}

\frac{a^{3} \sqrt{3}}{2}

\frac{a^{3} \sqrt{2}}{2}

Câu 39: 1 điểm

Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, cạnh bên tạo với mặt phẳng đáy một góc bằng 45°. Hình chiếu của A trên mặt phẳng (A’B’C’) trùng với trung điểm của A’B’. Tính thể tích V của khối lăng trụ theo a.

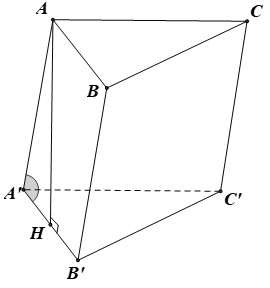
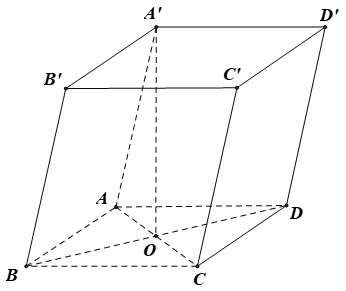
Hình ảnh

V = \frac{a^{3} \sqrt{3}}{2}

V = \frac{a^{3} \sqrt{3}}{8}

V = \frac{a^{3} \sqrt{3}}{16}

V = \frac{a^{3} \sqrt{3}}{24}

Câu 40: 1 điểm

Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD ^ = 120° và AA' = 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

Hình ảnh

V = 12 $a^{3}$

V = 3 $a^{3}$

V = 9 $a^{3}$

V = 6

a^{3}

Xem thêm đề thi tương tự

80 câu trắc nghiệm Khối đa diện nâng caoLớp 12Toán

Chương 1: Khối đa diện
Ôn tập Toán 12 Chương 1 Hình học
Lớp 12;Toán

78 câu hỏi 4 mã đề 1 giờ

150,693 lượt xem 81,137 lượt làm bài

Chưa chinh phục!!!

80 câu trắc nghiệm Vectơ cơ bảnLớp 10Toán

Chương 1: Vectơ
Ôn tập Toán 10 Chương 1 Hình học
Lớp 10;Toán

82 câu hỏi 4 mã đề 1 giờ

170,713 lượt xem 91,917 lượt làm bài

Chưa chinh phục!!!

Đề thi Vật Lý Sở Thanh Hóa.docxVật lý

/Môn Lý/Đề thi Vật Lý các trường, sở 2023

40 câu hỏi 1 mã đề 50 phút

1,128 lượt xem 560 lượt làm bài

Chưa chinh phục!!!

80. ĐỀ THI THỬ TN THPT 2023 - MÔN TIẾNG ANH - Cụm 7 trường THPT Hải Dương (Bản word có lời giải chi tiết).docxTHPT Quốc giaTiếng Anh

/Môn Tiếng Anh/Đề thi thử Tiếng Anh 2023 các trường, sở

50 câu hỏi 1 mã đề 40 phút

3,535 lượt xem 1,883 lượt làm bài

Chưa chinh phục!!!

80. Đề thi thử TN THPT VẬT LÝ 2024 - Kỳ Anh - Hà Tĩnh. (Có lời giải chi tiết)THPT Quốc giaVật lý

/Môn Lý/Đề thi Vật Lý các trường, sở 2024

40 câu hỏi 1 mã đề 50 phút

5,896 lượt xem 3,136 lượt làm bài

Chưa chinh phục!!!

80. Đề thi thử TN THPT môn Toán năm 2024 - Sở Hà Tĩnh - Lần 3THPT Quốc giaToán

/Môn Toán/Đề thi thử Toán 2024 các trường, sở

50 câu hỏi 1 mã đề 1 giờ 30 phút

4,209 lượt xem 2,226 lượt làm bài

Chưa chinh phục!!!

Recent IELTS Reading Actual test 80

Chưa có mô tả

40 câu hỏi 1 mã đề 1 giờ

214,372 lượt xem 115,423 lượt làm bài

Chưa chinh phục!!!

Đề thi thử THPT QG năm 2021 môn Toán - Bộ đề 80THPT Quốc giaToán

Đề thi thử THPT Quốc gia môn Toán năm 2021, được biên soạn theo cấu trúc chuẩn của Bộ Giáo dục. Nội dung bao gồm các dạng bài trọng tâm như giải tích, logarit, và bài toán thực tế, là tài liệu hữu ích cho học sinh lớp 12 ôn tập hiệu quả.

50 câu hỏi 1 mã đề 1 giờ

105,979 lượt xem 57,064 lượt làm bài

Chưa chinh phục!!!

Đề thi thử tốt nghiệp THPT QG môn Vật Lý năm 2020 - Mã đề 80THPT Quốc giaVật lý

Đề thi thử tốt nghiệp THPT Quốc Gia năm 2020 môn Vật Lý, nội dung sát thực tế, phù hợp ôn thi tốt nghiệp.

40 câu hỏi 1 mã đề 1 giờ

130,363 lượt xem 70,189 lượt làm bài

Chưa chinh phục!!!

LetQA - Nền tảng trắc nghiệm & đề thi đa lĩnh vực

Về chúng tôi

LetQA là công cụ hỗ trợ học sinh, sinh viên, giáo viên, tổ chức trong việc ôn luyện, kiểm tra kiến thức; được cung cấp miễn phí cho tất cả người dùng.
LetQA không cung cấp dịch vụ mạng xã hội, không cung cấp thông tin tổng hợp và không thu phí người dùng.

Thông tin liên hệ & hỗ trợ

Email: hotro@letqa.com

Facebook: Let QA (fb.com/letqavn)

Liên kết phổ biến

Yêu cầu bổ sung đề thi

Đóng góp đề thi

Website liên kết

Phần mềm kiểm tra trùng lặp Kiểm Tra Tài Liệu

Phần mềm xuất bản tạp chí điện tử VOJS

Công cụ kiểm tra chính tả và thể thức Viver

Công cụ hỗ trợ trích dẫn và phân tích khoa học Scholar Hub