Trắc nghiệm ôn thi THPT Quốc gia môn toán: Hàm số mũ và logarit

Cho hai số thực dương x,y thỏa mãn 2^x + 2^y = 4. Tìm giá trị lớn nhất P_max  của biểu thức

P = (2x² + y)(2y² + x) + 9xy.

Số nghiệm của phương trình

$(x^2-4)({\log }_{2}x+{\log }_{3}x+{\log }_4 x+...{\log }_{19} x-{\log }_{20}^{2}x) = 0$ là:

Cho hàm số y = log₃(2x+1), ta có

Cho ${\log }_{a}c=\frac{1}{3}$; ${\log }_{b}c=5$ với a,b là các số thực lớn hơn 1. Khi đó log_ab c là:

Hàm số y = ln(x² – 2x + m) có tập xác định là $\mathrm{ℝ}$ khi:

Số nghiệm của phương trình 9^x + 2(x – 2).3^x + 2x – 5 = 0 là:

Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình:  $(x+1){\log }_{\frac{1}{2}}^{2}x+(2x+5){\log }_{\frac{1}{2}}x+6\ge 0$ là:

Tập xác định D của hàm số $y=x^{\frac{1}{3}}$ là:

Cho a, b là các số thực dương thỏa mãn $a\ne 0; a\ne b$. Mệnh đề nào sau đây đúng?

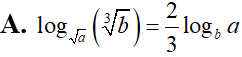
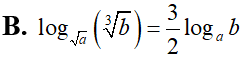
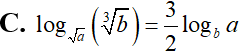
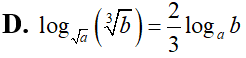
Tập nghiệm của bất phương trình ${\left(\frac{\pi }{4}\right)}^{\frac{1}{x}}>{\left(\frac{\mathrm{\pi }}{4}\right)}^{\frac{3}{x}+5}$ là:

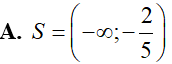
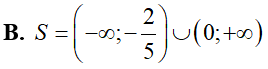
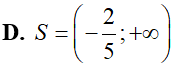
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích là 36, đường thẳng chứa cạnh AB song song với Ox, các đỉnh A, B, C lần lượt nằm trên các đồ thị hàm số y = log_a x, $y={\log }_{\sqrt{a}}x$, $y={\log }_{\sqrt[3]{a}}x$ với a là số thực lớn hơn 1. Tìm a.

Cho hàm số $y=5^{-x^2+6x-8}$. Gọi m là giá trị thực để y’(2) = 6mln5. Mệnh đề nào dưới đây đúng?

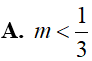
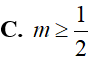
Cho phương trình $4{\log }_9^{2}x+m.{\log }_{\frac{1}{3}}x+\frac{1}{6}{\log }_{\frac{1}{\sqrt{3}}}x+m-\frac{2}{9}=0$. Tìm tham số m để phương trình có 2 nghiệm x₁, x₂ thỏa mãn x₁.x₂ = 3.

Cho log₉ x = log₁₂ y=log₁₆ (x+y). Giá trị của tỉ số $\frac{x}{y}$ là:

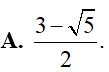
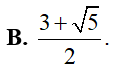
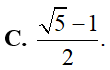
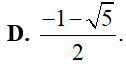
Tổng các nghiệm của phương trình ${\log }_3(2x+1)-{\log }_{\frac{1}{3}}(3-x)=0$ là:

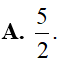
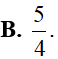
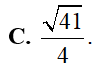
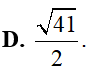
Cho bất phương trình ${(\sqrt{10}+1)}^{{\log }_{3}x}-{(\sqrt{10}-1)}^{{\log }_{3}x}\ge \frac{2x}{3}$. Đặt $t={\left(\frac{\sqrt{10}+1}{3}\right)}^{{\log }_{3}x}$ ta được bất phương trình nào sau đây?

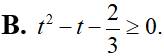
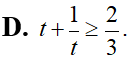
Giải bất phương trình log₄(x² – x – 8) < 1 + log₃ x được tập nghiệm là một khoảng trên trục số có độ dài là:

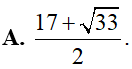
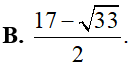
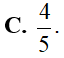
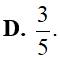
Khẳng định nào sau đây là sai?

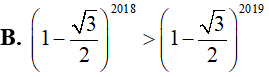
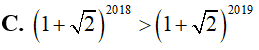
Giá trị của m để phương trình $4^{\left.x\right|}-2^{\left.x\right|+1}-m=0$ có nghiệm duy nhất là:

Tập nghiệm của bất phương trình  ${\log }^{2}x-\log x^3+2\ge 0$  là $S=(a;b]\cup [c;+\infty )$ thì a + b + c là:

Cho hàm số $y=\ln \frac{1}{x}$. Hệ thức nào sau đây đúng?

Số nghiệm nguyên của bất phương trình ${\log }_2(x - 1) \le 2$ là:

Cho a, b, c dương thỏa mãn 2^a = 3^b = 18^c. Khi đó biểu thức $T = \frac{b}{c}-\frac{b}{a}$ có giá trị là:

Trong các hàm số dưới đây, hàm số nào đồng biến trên  $\mathrm{ℝ}$.

Cho các số thực dương a, b, c với $c\ne 1$. Khẳng định nào sau đây sai?

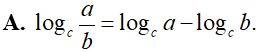
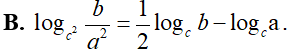
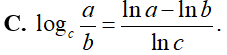
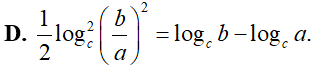
Cho n > 1 là một số nguyên. Giá trị biểu thức $\frac{1}{{\log }_2 n!}+\frac{1}{{\log }_3 n!}+...+\frac{1}{{\log }_n n!}$ bằng:

Tập nghiệm S của bất phương trình ${(17-12\sqrt{2})}^x\le {(3+\sqrt{8})}^{x^2}$là:

Cho 9^x + 9^–x = 23. Tính 3^x + 3^–x.

Cho x, y là các số thực lớn hơn 1 thỏa mãn x² + 9y² = 6xy. Tính  $M=\frac{1+{\log }_{12} x+{\log }_{12} y}{2.{\log }_{12} (x+3y)}$.

Phương trình log₂ (x – 1) = 2 có nghiệm là: