Ở mặt chất lỏng, tại hai điểm
và
có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng
, trên đoạn thẳng
có 23 điểm cực đại giao thoa.
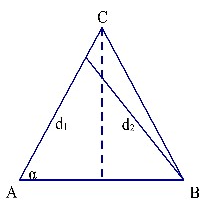
là điểm trên mặt chất lỏng mà
là tam giác cân tại C. Biết
Trên đoạn
có hai điểm cực đại giao thoa liên tiếp mà phần tử chất lỏng tại đó dao động cùng pha với nhau. Đoạn thẳng
có độ dài gần nhất với giá trị nào sau đây?
A.
B.
C.
D.
Đáp án đúng là: C
Ở mặt chất lỏng, tại hai điểm và có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng , trên đoạn thẳng có 23 điểm cực đại giao thoa. là điểm trên mặt chất lỏng mà là tam giác cân tại C. Biết Trên đoạn có hai điểm cực đại giao thoa liên tiếp mà phần tử chất lỏng tại đó dao động cùng pha với nhau. Đoạn thẳng có độ dài gần nhất với giá trị nào sau đây?
Đáp án đúng là: C
ĐK cực đại
( là số nguyên và là số thực)
. Chuẩn hóa
Cực đại bậc và cùng pha với nhau thì lẻ
Trên AB có 23 cực đại nên mỗi bên có 11 cực đại . Dùng TABLE
| là số lẻ nằm giữa và | |||
| -11 | 0,4583 | 0,5172 | |
| … | … | … | |
| -2 | 2,9409 | 3,0669 | |
| -1 | 4,2777 | 4,3448 |
Shift solve với . Chọn C
Câu hỏi tương tự:
#4817 THPT Quốc giaVật lý
Ở mặt chẩt lỏng, tại hai điểm A và B cách nhau 30 cm có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp. Gọi ∆ là đường thẳng ở mặt chất lỏng vuông góc với đoạn thẳng AB và cách trung trực của AB 6 cm. Biết số điểm cực đại giao thoa trên ∆ là 5. Số điểm cực đại giao thoa trên đoạn thẳng AB là
Lượt xem: 82,065 Cập nhật lúc: 18:19 25/04/2025
#952 THPT Quốc giaVật lý
Ở mặt chất lỏng, tại hai điểm và có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng , trên đoạn thẳng có 23 điểm cực đại giao thoa. là điểm trên mặt chất lỏng mà là tam giác cân tại C. Biết Trên đoạn có hai điểm cực đại giao thoa liên tiếp mà phần tử chất lỏng tại đó dao động cùng pha với nhau. Đoạn thẳng có độ dài gần nhất với giá trị là
Lượt xem: 16,350 Cập nhật lúc: 02:08 23/04/2025
#11410 Vật lýĐGNL ĐH Quốc gia TP.HCM
Ở mặt chất lỏng, tại hai điểm A và B cách nhau 11cm có hai nguồn sóng kết hợp, dao động điều hòa, cùng pha theo phương thẳng đứng có phương trình
. Sóng lan truyền có tốc độ 40cm/s và biên độ mỗi sóng không đổi khi truyền đi. Điểm M thuộc mặt chất lỏng, nằm trên đường trung
trực của AB dao động ngược pha với nguồn. Khoảng cách nhỏ nhất từ M đến A bằng
Lượt xem: 194,417 Cập nhật lúc: 18:07 23/04/2025
#471 THPT Quốc giaVật lý
Ở mặt chất lỏng, tại hai điểm và có hai nguồn dao động cùng pha theo phương thẳng đứng phát ra hai sóng kết hợp có bước sóng . là một điểm trên mặt chất lỏng sao cho là tam giác đều. Trên đoạn thẳng có 5 cực đại giao thoa, tính từ lần lượt là và . Biết các phần tử ở và dao động ngược pha. Đoạn thẳng có độ dài gần nhất với giá trị nào sau đây?
Lượt xem: 8,146 Cập nhật lúc: 01:42 26/04/2025
#584 THPT Quốc giaVật lý
Ở mặt chất lỏng, hai nguồn sóng tại hai điểm và cách nhau phát ra hai sóng kết hợp có phương trinh là , truyền với tốc độ . Coi biên độ sóng không giảm. Trên đoạn , số điểm cực đại và cực tiểu giao thoa lần lượt là
Lượt xem: 10,102 Cập nhật lúc: 23:23 23/04/2025
#832 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại hai điểm và , dao động cùng pha theo phương thẳng đứng tạo ra hai sóng lan truyền trên mặt chất lỏng với bước sóng . Gọi là trung điểm của đoạn thẳng . Trên , điểm là cực đại giao thoa gần nhất. Trên đường trung trực của , điểm là điểm gần nhất mà phần tử ở đó dao động ngược pha với dao động của phần tử ở . Biết . Mặt khác, trên nửa đường thẳng xuất phát từ và vuông góc với có điểm và điểm là các cực tiểu giao thoa, giữa và có hai cực đại giao thoa, . Giá trị của gần nhất với giá trị nào sau đây?
Lượt xem: 14,262 Cập nhật lúc: 11:59 24/04/2025
#824 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại hai điểm và , dao động cùng pha theo phương thẳng đứng với tần số . Sóng truyền trên mặt chất lỏng có bước sóng . Ở mặt chất lỏng, điểm là cực đại giao thoa cách và những khoảng và . Biết tốc độ truyền sóng trên mặt chất lỏng có giá trị trong khoảng từ đến . Giá trị của là
Lượt xem: 14,174 Cập nhật lúc: 21:58 24/04/2025
#2757 THPT Quốc giaVật lý
Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại hai điểm và cách nhau dao động cùng pha theo phương thẳng đứng, phát ra hai sóng lan truyền trên mặt chất lỏng với bước sóng . Gọi ( ) là một đường thẳng nằm ở mặt chất lỏng vuông góc với tại điểm . Biết . Số điểm dao động với biên độ cực đại trên ( ) là
Lượt xem: 46,968 Cập nhật lúc: 18:05 25/04/2025
#6616 THPT Quốc giaVật lý
Tại hai điểm và cách nhau ở mặt chất lỏng có hai nguồn sóng dao động đồng bộ theo phương thẳng đứng với tần số . Tốc độ truyền sóng trên mặt chất lỏng là với . Lục giác đều thuộc mặt chất lỏng, các phần tử tại dao động với biên độ cực đại. Điểm thuộc đoạn , gần nhất mà phần tử ở đó thuộc vân giao thoa cực đại. Khoảng cách có giá trị gần nhất với giá trị nào sau đây?
Lượt xem: 112,566 Cập nhật lúc: 17:54 25/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 40 câu hỏi 50 phút
6,154 xem464 thi
