Cho hàm số $f \left( x \right)$ có đạo hàm trên $\mathbb{R}$, đồng thời thỏa mãn $x f \left( x \right) = \sqrt{x^{2} + 1} \left(\right. 1 - f^{'} \left( x \right) \sqrt{x^{2} + 1} \left.\right)$ và $f \left( 0 \right) = 1$. Tính giá trị của $f \left( 1 \right)$.

A.  

$\sqrt{2}$.

B.  

$\dfrac{1}{\sqrt{2}}$.

C.  

2.

D.  

1.

Đáp án đúng là: A

Cho hàm số $f \left( x \right)$ có đạo hàm $f^{'} \left( x \right) = \left( x^{2} - x \right)^{2} - 4 x \left( x^{2} + 1 \right) + 8 x^{2}$. Có bao nhiêu giá trị nguyên của $m \in \left( - 10 ; 10 \right)$ để hàm số $g \left( x \right) = f \left( x^{2} - 2 x + m \right)$ đồng biến trên $\left( 1 ; + \infty \right)$?
A. 6. B. 5. C. 16. D. 15.
Lời giải
Chọn B
$f^{'} \left( x \right) = \left( x^{2} - x \right)^{2} - 4 x \left( x^{2} + 1 \right) + 8 x^{2} = \left( x^{2} - x \right)^{2} - 4 x \left( x - 1 \right)^{2} = \left( x - 1 \right)^{2} \left( x^{2} - 4 x \right) .$
$f^{'} \left( x \right) \geq 0 \Leftrightarrow \left( x - 1 \right)^{2} \left( x^{2} - 4 x \right) \geq 0 \Leftrightarrow \left[\right. x \geq 4 \\ x \leq 0 \\ x = 1 .$ $g \left( x \right) = f \left( x^{2} - 2 x + m \right) \Rightarrow g^{'} \left( x \right) = 2 \left( x - 1 \right) . f^{'} \left( x^{2} - 2 x + m \right) .$
Để hàm số $g \left( x \right) = f \left( x^{2} - 2 x + m \right)$ đồng biến trên $\left( 1 ; + \infty \right) \Rightarrow f ' \left( x^{2} - 2 x + m \right) \geq 0$
$\Leftrightarrow \left[\right. x^{2} - 2 x + m \geq 4 , \forall x \in \left( 1 ; + \infty \right) \\ x^{2} - 2 x + m \leq 0 , \forall x \in \left( 1 ; + \infty \right) \Leftrightarrow \left[\right. x^{2} - 2 x \geq 4 - m , \forall x \in \left( 1 ; + \infty \right) \\ x^{2} - 2 x \leq - m , \forall x \in \left( 1 ; + \infty \right) .$
Đặt $h \left( x \right) = x^{2} - 2 x , x \in \left( 1 ; + \infty \right) \Rightarrow h^{'} \left( x \right) = 2 x - 2 > 0 , \forall x > 1 .$

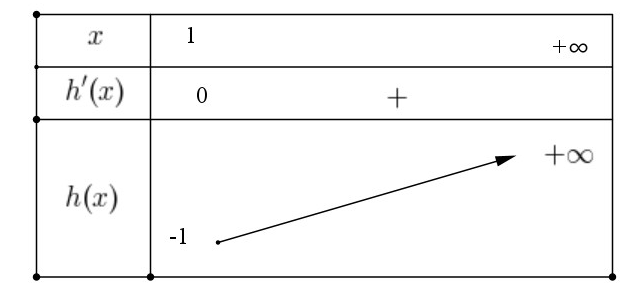
+ Trường hợp 1: $x^{2} - 2 x \geq 4 - m , \forall x \in \left( 1 ; + \infty \right) \Leftrightarrow - 1 \geq 4 - m \Leftrightarrow m \geq 5 .$
Do $\left{\right. m \in \left( - 10 ; 10 \right) \\ m \geq 5 \\ m \in \mathbb{Z} \Rightarrow m \in \left{ 5 , 6 , 7 , 8 , 9 \right} .$
+ Trường hợp 2: $x^{2} - 2 x \leq - m , \forall x \in \left( 1 ; + \infty \right) \Leftrightarrow m = \emptyset .$
Do đó có 5 giá trị của $m .$