Cho hàm số
liên tục trên
và có bảng xét dấu của
như sau:
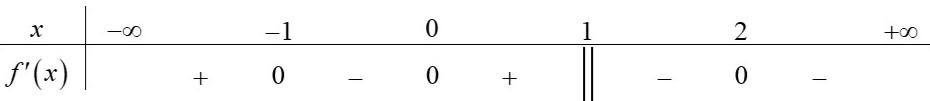
Số điểm cực đại của hàm số đã cho là
A. 4.
B. 1.
C. 2.
D. 3.
Đáp án đúng là: C
Cho hàm số
liên tục trên
và có bảng xét dấu của
như sau:
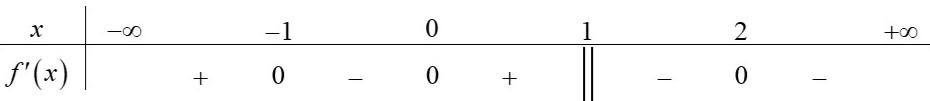
Số điểm cực đại của hàm số đã cho là
4.
1.
2.
3.
Đáp án đúng là: C
Do hàm số
liên tục trên
,
,
không xác định nhưng do hàm số liên tục trên
nên tồn tại
và
đổi dấu từ
sang
khi đi qua các điểm
,
nên hàm số đã cho đạt cực đại tại 2 điểm này.
Vậy số điểm cực đại của hàm số đã cho là 2.
Câu hỏi tương tự:
#7838 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng xét dấu của
như sau:
Số điểm cực đại của hàm số đã cho bằng
Lượt xem: 133,406 Cập nhật lúc: 02:33 26/04/2025
#8421 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng xét dấu
như sau:
Hàm số có bao nhiêu điểm cực trị
Lượt xem: 143,246 Cập nhật lúc: 11:44 26/04/2025
#8497 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là
Lượt xem: 144,533 Cập nhật lúc: 10:56 26/04/2025
#7909 THPT Quốc giaToán
Cho hàm số
liên tục trên
và hàm số
có bảng xét dấu như sau:
Có bao nhiêu số nguyên ; 2023] để hàm số có ít nhất 5 điểm cực trị?
Lượt xem: 134,628 Cập nhật lúc: 01:54 25/04/2025
#8658 THPT Quốc giaToán
Cho hàm số
có
có đạo hàm liên tục trên
và bảng xét dấu đạo hàm như sau
Hàm số có bao nhiêu điểm cực trị?
Lượt xem: 147,360 Cập nhật lúc: 14:36 26/04/2025
#8022 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 136,518 Cập nhật lúc: 11:41 26/04/2025
#11396 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có bảng biến thiên như hình vẽ bên dưới.
Có tất cả bao nhiêu giá trị thực của tham số thuộc đoạn để giá trị lớn nhất của hàm số có giá trị lớn nhất trên đoạn bằng ?
Lượt xem: 193,877 Cập nhật lúc: 12:35 26/04/2025
#7856 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có bảng biến thiên như hình sau:
Có bao nhiêu giá trị nguyên dương của tham số để bất phương trình nghiệm đúng với mọi
Lượt xem: 133,719 Cập nhật lúc: 23:56 23/04/2025
#11376 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có đồ thị như hình vẽ bên dưới. Gọi
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
. Ta có
bằng:
Lượt xem: 193,540 Cập nhật lúc: 12:18 26/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 51 câu hỏi 1 giờ 30 phút
4,963 xem363 thi
