Cho hàm số
liên tục trên
và có bảng xét dấu
như sau:
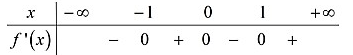
Hàm số
có bao nhiêu điểm cực trị
A. 6 .
B. 7 .
C. 8 .
D. 9 .
Đáp án đúng là: A
Cho hàm số
liên tục trên
và có bảng xét dấu
như sau:
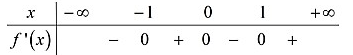
Hàm số có bao nhiêu điểm cực trị
6 .
7 .
8 .
9 .
Đáp án đúng là: A
(VDC):
Phương pháp:
Đưa hàm số
. Để hàm số
có ít nhất 5 điểm cực trị thì hàm số
phải có ít nhất 2 điểm cực trị dương.
Tìm điều kiện để phương trình
có ít nhất 2 nghiệm dương phân biệt. Sử dụng tương giao đồ thị hàm số.
Cách giải
Ta có:
Xét hàm số
.
Để hàm số
có ít nhất 5 điểm cực trị thì hàm số
phải có ít nhất 2 điểm cực trị dương.
Phương trình
phải có ít nhất 2 nghiệm dương phân biệt.
Ta có:
.
Do
.
Dựa vào BBT ta thấy
.
Xét hàm số
.
Hàm số
đồng biến trên
.
Ta có BBT:
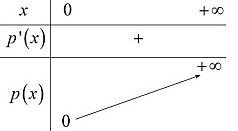
Dựa vào ta thấy để phương trình có ít nhất 2 nghiệm dương thì
Kết hợp điều kiện đề bài nên có 2024 giá trị m thoả mãn.
Câu hỏi tương tự:
#8363 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng xét dấu của
như sau:
Số điểm cực đại của hàm số đã cho là
Lượt xem: 142,321 Cập nhật lúc: 01:52 11/05/2025
#7838 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng xét dấu của
như sau:
Số điểm cực đại của hàm số đã cho bằng
Lượt xem: 133,415 Cập nhật lúc: 19:36 12/05/2025
#8497 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng xét dấu của đạo hàm như sau
Số điểm cực trị của hàm số đã cho là
Lượt xem: 144,540 Cập nhật lúc: 07:42 17/05/2025
#7909 THPT Quốc giaToán
Cho hàm số
liên tục trên
và hàm số
có bảng xét dấu như sau:
Có bao nhiêu số nguyên ; 2023] để hàm số có ít nhất 5 điểm cực trị?
Lượt xem: 134,639 Cập nhật lúc: 23:41 12/05/2025
#8658 THPT Quốc giaToán
Cho hàm số
có
có đạo hàm liên tục trên
và bảng xét dấu đạo hàm như sau
Hàm số có bao nhiêu điểm cực trị?
Lượt xem: 147,376 Cập nhật lúc: 12:24 16/05/2025
#8022 THPT Quốc giaToán
Cho hàm số
liên tục trên
và có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Lượt xem: 136,529 Cập nhật lúc: 10:32 17/05/2025
#11396 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có bảng biến thiên như hình vẽ bên dưới.
Có tất cả bao nhiêu giá trị thực của tham số thuộc đoạn để giá trị lớn nhất của hàm số có giá trị lớn nhất trên đoạn bằng ?
Lượt xem: 193,883 Cập nhật lúc: 09:40 17/05/2025
#7856 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có bảng biến thiên như hình sau:
Có bao nhiêu giá trị nguyên dương của tham số để bất phương trình nghiệm đúng với mọi
Lượt xem: 133,731 Cập nhật lúc: 06:09 14/05/2025
#11376 THPT Quốc giaToán
Cho hàm số
liên tục trên đoạn
và có đồ thị như hình vẽ bên dưới. Gọi
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn
. Ta có
bằng:
Lượt xem: 193,546 Cập nhật lúc: 10:38 17/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
5,143 xem384 thi
