Cho hàm số
có đạo hàm cấp hai liên tục trên
, biết rằng
và hàm số
là hàm số bậc ba có đồ thị như hình vẽ.
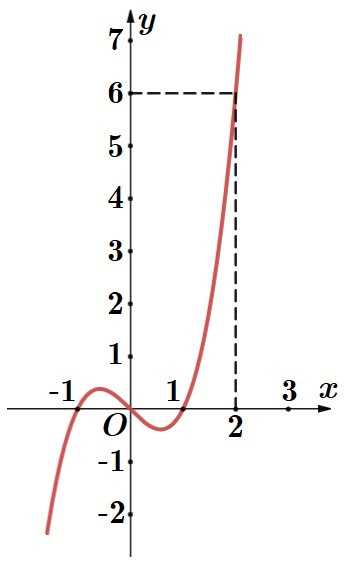
Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đồ thị hàm số
,
khi quay quanh trục
có giá trị nằm trong khoảng nào sau đây?
A.
.
B.
.
C.
.
D.
.
Đáp án đúng là: B
Cho hàm số
có đạo hàm cấp hai liên tục trên
, biết rằng
và hàm số
là hàm số bậc ba có đồ thị như hình vẽ.

Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đồ thị hàm số , khi quay quanh trục có giá trị nằm trong khoảng nào sau đây?
.
.
.
.
Đáp án đúng là: B
Cho hàm số
có đạo hàm cấp hai liên tục trên
, biết rằng
và hàm số
là hàm số bậc ba có đồ thị như hình vẽ.
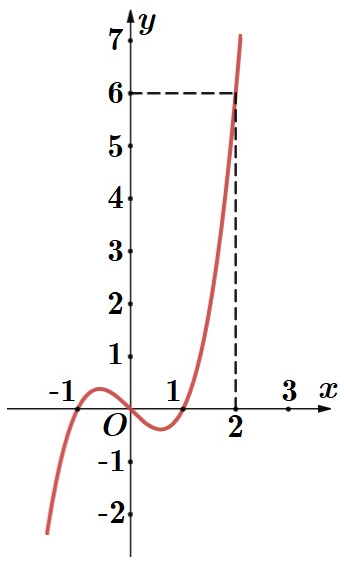
Thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi các đồ thị hàm số , khi quay quanh trục có giá trị nằm trong khoảng nào sau đây?
A. . B. . C. . D. .
Lời giải
Từ đồ thị ta thấy được , mà đồ thị đi qua điểm .
Đặt do . Khi đó và .
Ta có
.
.
Xét phương trình hoành độ giao điểm: .
Khi đó (đvtt).
Câu hỏi tương tự:
#7586 THPT Quốc giaToán
Cho hàm số
luôn nhận giá trị dương và có đạo hàm đến cấp hai trên khoảng đồng thời thỏa mãn điều kiện và . Tính giá trị .Lượt xem: 129,124 Cập nhật lúc: 14:40 09/05/2025
#7521 THPT Quốc giaToán
Cho hàm số có đạo hàm trên . Nếu hàm số đã cho có đúng hai điểm cực trị là – 1 và 2 thì hàm số có tất cả bao nhiêu điểm cực trị?
Lượt xem: 127,947 Cập nhật lúc: 17:59 10/05/2025
#8987 THPT Quốc giaToán
Cho hàm số có đạo hàm là . Có bao nhiêu giá trị nguyên của tham số để hàm số có đúng 9 điểm cực trị?
Lượt xem: 152,989 Cập nhật lúc: 22:39 13/05/2025
#8251 THPT Quốc giaToán
Cho hàm số
có đạo hàm trên
, đồ thị hàm số
như trong hình vẽ bên.
Hỏi phương trình có tất cả bao nhiêu nghiệm biết ?
Lượt xem: 140,431 Cập nhật lúc: 16:10 15/05/2025
#8131 THPT Quốc giaToán
Cho hàm số có đạo hàm . Tính tổng các giá trị nguyên của tham số để hàm số có đúng điểm cực trị
Lượt xem: 138,393 Cập nhật lúc: 16:36 16/05/2025
#7746 THPT Quốc giaToán
Cho hàm số có đạo hàm . Số điểm cực trị của hàm số đã cho bằng
Lượt xem: 131,824 Cập nhật lúc: 18:18 13/05/2025
#8298 THPT Quốc giaToán
Cho hàm số có đạo hàm . Tìm số điểm cực trị của hàm số đã cho.
Lượt xem: 141,236 Cập nhật lúc: 06:38 14/05/2025
#7997 THPT Quốc giaToán
Cho hàm số có đạo hàm Số điểm cực trị của đồ thị hàm số là
Lượt xem: 136,116 Cập nhật lúc: 06:42 15/05/2025
#7598 THPT Quốc giaToán
Cho hàm số có đạo hàm với mọi . Có bao nhiêu số nguyên dương để hàm số đồng biến trên khoảng ?
Lượt xem: 129,336 Cập nhật lúc: 07:39 15/05/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
1,624 xem111 thi
