Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8872

Cho hàm số y=f(x)y = f \left( x \right) xác định trên R\mathbb{R} và có đạo hàm f′(x)=12x(x+1)(3−x)27,∀x∈Rf^{'} \left( x \right) = 12 x \left( x + 1 \right) \left( 3 - x \right)^{27} , \forall x \in \mathbb{R}. Hàm số đã cho nghịch biến trên khoảng nào sau đây?

A.  

(−1;3)\left( - 1 ; 3 \right).

B.  

(−∞;−1)\left( - \infty ; - 1 \right).

C.  

(3;+∞)\left( 3 ; + \infty \right).

D.  

(−∞;0)\left( - \infty ; 0 \right).

Đáp án đúng là: C

Ta có f′(x)=0⇔12x(x+1)(3−x)27=0⇔[x=0x=−1x=3f^{'} \left( x \right) = 0 \Leftrightarrow 12 x \left( x + 1 \right) \left( 3 - x \right)^{27} = 0 \Leftrightarrow \left[\right. x = 0 \\ x = - 1 \\ x = 3.
Bảng xét dấu



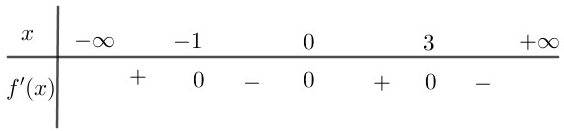
Hàm số đã cho nghịch biến trên khoảng (3;+∞)\left( 3 ; + \infty \right).


 

Câu hỏi tương tự:

#11166 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) xác định trên R\mathbb{R} và có đạo hàm f′(x)=(x2−3x)(1−x())2f^{'} \left( x \right) = \left( x^{2} - 3 x \right) \left( 1 - x \left(\right)\right)^{2}. Hàm số f(x)f \left( x \right) nghịch biến trên khoảng nào dưới đây

Lượt xem: 189,895 Cập nhật lúc: 16:06 17/01/2025

#8206 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) xác định và có đạo hàm trên và có bảng biến thiên như sau



Đồ thị hàm số f(x)f \left( x \right) có bao nhiêu đường tiệm cận?

Lượt xem: 139,540 Cập nhật lúc: 05:27 07/01/2025

#7691 THPT Quốc giaToán

Cho hàm số f(x)f \left( x \right) có đạo hàm xác định trên R\mathbb{R} thỏa mãn f(0)=22f \left( 0 \right) = 2 \sqrt{2}, f(x)>0f \left( x \right) > 0 và f(x).f′(x)=(2x+1)1+f2(x) , ∀x∈Rf \left( x \right) . f^{'} \left( x \right) = \left( 2 x + 1 \right) \sqrt{1 + f^{2} \left( x \right)} \textrm{ } , \textrm{ } \forall x \in \mathbb{R}. Giá trị f(2)f \left( 2 \right) là

Lượt xem: 130,793 Cập nhật lúc: 03:03 18/01/2025

#8044 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) liên tục và xác định trên RRcó đồ thị đạo hàm f′(x)f ' \left( x \right) được cho như hình vẽ. Hàm số y=f(x2−1)y = f \left( x^{2} - 1 \right) đồng biến trên khoảng nào sau đây?


Lượt xem: 136,851 Cập nhật lúc: 01:36 17/01/2025

#7955 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) xác định trên R\mathbb{R} và có bảng biến thiên như hình vẽ sau:



Giá trị cực tiểu của hàm số đã cho bằng

Lượt xem: 135,313 Cập nhật lúc: 00:37 16/01/2025

#8045 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) xác định trên R\mathbb{R}và có bảng xét dấu:



Hàm số

có bao nhiêu điểm cực trị?

Lượt xem: 136,802 Cập nhật lúc: 23:42 07/01/2025

#8942 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) xác định trên R\mathbb{R} và có bảng biến thiên như hình vẽ bên. Đồ thị hàm số y=2f(x)+3y = 2 f \left( x \right) + 3 cắt trục hoành tại bao nhiêu điểm?

Lượt xem: 152,055 Cập nhật lúc: 03:53 09/01/2025

#8255 THPT Quốc giaToán

Cho hàm số  y=f(x)y = f \left( x \right) xác định trên  R∖{−1}\mathbb{R} \setminus \{ -1 \} và có bảng biến thiên như hình vẽ:
 



Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là:

 

Lượt xem: 140,407 Cập nhật lúc: 23:12 15/01/2025

#8076 THPT Quốc giaToán

Cho hàm số y=f(x)y = f \left( x \right) xác định và liên tục trên R\mathbb{R} và có bảng biến thiên như sau:



Mệnh đề nào sau đây là đúng?

Lượt xem: 137,342 Cập nhật lúc: 06:49 16/01/2025


Đề thi chứa câu hỏi này:

30. Đề thi thử TN THPT môn Toán năm 2024 - THPT CẨM THỦY 1 L1.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,903 lượt xem 2,576 lượt làm bài