Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7562

Cho hình chóp S.ABCS . A B C, có SAS A vuông góc mặt phẳng (ABC)\left( A B C \right); tam giác ABCA B C vuông tại BB. Biết SA=2aS A = 2 a, AB=aA B = a, BC=a3B C = a \sqrt{3}. Tính diện tích của mặt cầu ngoại tiếp hình chóp.

A.  

8πa28 \pi a^{2}.

B.  

32πa232 \pi a^{2}.

C.  

16πa216 \pi a^{2}.

D.  

4πa24 \pi a^{2}.

Đáp án đúng là: A

Cho hình chóp S.ABCS . A B C, có SAS A vuông góc mặt phẳng (ABC)\left( A B C \right); tam giác ABCA B C vuông tại BB. Biết SA=2aS A = 2 a, AB=aA B = a, BC=a3B C = a \sqrt{3}. Tính diện tích của mặt cầu ngoại tiếp hình chóp.
A. 8πa28 \pi a^{2}. B. 32πa232 \pi a^{2}. C. 16πa216 \pi a^{2}. D. 4πa24 \pi a^{2}.
Lời giải



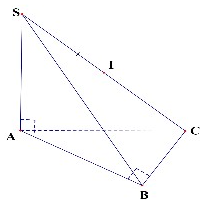
+ Từ giả thiết ta có: (1)
+ Lại có: SA⊥(ABC)⇒SA⊥AC⇒SAC^=90∘S A \bot \left( A B C \right) \Rightarrow S A \bot A C \Rightarrow \hat{S A C} = 90 \circ (2)
+ Từ (1) và (2) ⇒SAC^=SBC^=90∘⇒\Rightarrow \hat{S A C} = \hat{S B C} = 90 \circ \RightarrowBốn điểm S, A, B, CS , \textrm{ } A , \textrm{ } B , \textrm{ } Ccùng nằm trên mặt cầu đường kính SCS C.
+ Gọi RRlà bán kính mặt cầu ngoại tiếp ⇒R=SC2\Rightarrow R = \dfrac{S C}{2}
+ AC=AB2+BC2=a2+3a2=2aA C = \sqrt{A B^{2} + B C^{2}} = \sqrt{a^{2} + 3 a^{2}} = 2 a
SC=SA2+AC2=4a2+4a2=2a2S C = \sqrt{S A^{2} + A C^{2}} = \sqrt{4 a^{2} + 4 a^{2}} = 2 a \sqrt{2} ⇒R=a2\Rightarrow R = a \sqrt{2}.
+ Diện tích của mặt cầu ngoại tiếp hình chóp là: S=4πR2=4π((a2))2=8πa2S = 4 \pi R^{2} = 4 \pi \left(\left( a \sqrt{2} \right)\right)^{2} = 8 \pi a^{2}.


 

Câu hỏi tương tự:

#7734 THPT Quốc giaToán

Cho hình chóp tam giác S.ABCS . A B C có SAS A vuông góc với mặt phẳng (ABC)\left( A B C \right), SA=aS A = a, tam giác ABCA B C vuông cân tại AA, AB=aA B = a. Thể tích hình chóp S.ABCS . A B C bằng

Lượt xem: 131,511 Cập nhật lúc: 19:26 18/01/2025

#8571 THPT Quốc giaToán

Cho hình chớp S.ABCS . A B C có đáy là tam giác đều cạnh a,SAa , S A vuông góc mặt phẳng đáy, SB=3aS B = \sqrt{3} a (tham khảo hình vẽ)



Khoảng cách từ trung điểm MM của SAS A đến mặt phẳng (SBC)\left( S B C \right) bằng

Lượt xem: 145,741 Cập nhật lúc: 08:22 17/01/2025

#7646 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có SAS A vuông góc với (ABC)\left( A B C \right), tam giác ABCA B C đều cạnh bằng a,  SA=a3a , \textrm{ }\textrm{ } S A = a \sqrt{3}. Góc giữa đường thẳng SCS C và mặt phẳng (ABC)\left( A B C \right) bằng


Lượt xem: 130,053 Cập nhật lúc: 19:40 18/01/2025

#7976 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABCA B C là tam giác vuông cân tại B,B , AB=2aA B = 2 a và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ CC đến mặt phẳng (SAB)\left( S A B \right) bằng

Lượt xem: 135,632 Cập nhật lúc: 05:53 14/01/2025

#8662 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy là tam giác vuông tại AA, AB=6aA B = 6 a, AC=4aA C = 4 a, SAS A vuông góc với mặt
phẳng đáy và SA=aS A = a. Gọi MM là trung điểm của ABA B. Khoảng cách giữa hai đường thẳng SMS M và
BCB C bằng

Lượt xem: 147,299 Cập nhật lúc: 22:55 18/01/2025

#7569 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình chữ nhật, AB=2aA B = 2 a, AD=3aA D = 3 a, mặt bên SABS A B là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SAB)\left( S A B \right) và (SCD)\left( S C D \right) bằng

Lượt xem: 128,716 Cập nhật lúc: 02:57 18/01/2025

#8875 THPT Quốc giaToán

Cho hình chóp S.ABCS . A B C có đáy ABC là tam giác vuông tại B. AB=a,BC=2a.A B = a , B C = \sqrt{2} a .SA vuông góc với mặt phẳng đáy và SA=aS A = a (tham khảo hình vẽ). Góc giữa SC và mặt phẳng đáy bằng

Lượt xem: 150,913 Cập nhật lúc: 15:17 17/01/2025

#7747 THPT Quốc giaToán

Cho hình chóp S.ABC\text{S} . \text{ABC} có đáy ABC\text{ABC} là tam giác đều cạnh a\text{a}, đường thẳng SA\text{SA} vuông góc với mặt phẳng đáy và SA=3a2\text{SA} = \dfrac{3 \text{a}}{2}. Góc giữa hai mặt phẳng và (ABC)\left( \text{ABC} \right) bằng

Lượt xem: 131,739 Cập nhật lúc: 05:45 17/01/2025

#7807 THPT Quốc giaToán

Cho hình chóp S⋅ABCDS \cdot A B C D có đáy ABCDA B C D là hình vuông cạnh aa. Biết tam giác SABS A B đều và nằm trong mặt phẳng vuông góc với đáy. Gọi MM là trung điểm của SDS D. Gọi α\alpha là góc giữa hai mặt phẳng (MBC)\left( M B C \right) và (ABCD)\left( A B C D \right). Tính cosα\text{cos} \alpha.

Lượt xem: 132,760 Cập nhật lúc: 23:00 18/01/2025


Đề thi chứa câu hỏi này:

ĐỀ THI THỬ TN THPT 2023 - MÔN TOÁN - THPT Liên Trường Hải Phòng - Lần 1 THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

478 lượt xem 203 lượt làm bài