Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #8796

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh a,a , cạnh bên SA=a6S A = a \sqrt{6} và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SCS C và mặt phẳng (ABCD)\left( A B C D \right) bằng

A.  

(45)o.\left(45\right)^{\text{o}} .

B.  

(30)o.\left(30\right)^{\text{o}} .

C.  

(90)o.\left(90\right)^{\text{o}} .

D.  

(60)o.\left(60\right)^{\text{o}} .

Đáp án đúng là: D

Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu vuông góc của nó lên mặt phẳng đó.
Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Cách giải:



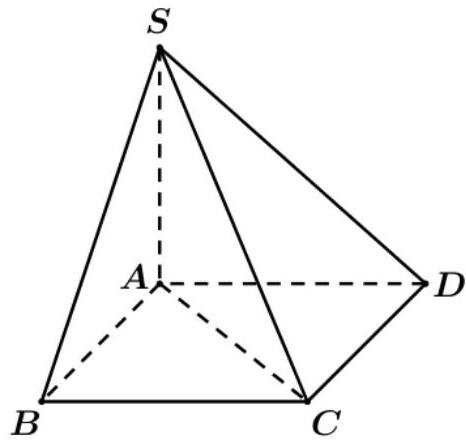
Ta có: SA⊥(ABCD)⇒(SC,(ABCD))=(SC,AC)=∠SCAS A \bot \left( A B C D \right) \Rightarrow \left(\right. S C , \left( A B C D \right) \left.\right) = \left( S C , A C \right) = \angle S C A
ABCD\text{ABCD} là hình vuông cạnh a nên AC=a2A C = a \sqrt{2}
Xét tam giác vuông SAC vuông tại A có: tan∠SCA=SAAC=a6a2=3⇒∠SCA=(60)@\text{tan} \angle S C A = \dfrac{S A}{A C} = \dfrac{a \sqrt{6}}{a \sqrt{2}} = \sqrt{3} \Rightarrow \angle S C A = \left(60\right)^{@}.


 

Câu hỏi tương tự:

#8923 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông cạnh aa. Biết SA⊥(ABCD)S A \bot \left( A B C D \right) và SA=a3S A = a \sqrt{3}. Thể tích của khối chóp S.ABCDS . A B C D là:

Lượt xem: 151,790 Cập nhật lúc: 18:28 18/01/2025

#7524 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh a,SA=2aa , S A = 2 a và SAS A vuông góc với đáy. Tính theo aa khoảng cách từ AA đến mặt phẳng (SBD)\left( S B D \right).

Lượt xem: 128,005 Cập nhật lúc: 18:26 18/01/2025

#8334 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông ABCDA B C D cạnh aa, cạnh bên SAS A vuông góc với mặt phẳng đáy và SA=a2S A = a \sqrt{2}. Thể tích của khối chóp S.ABCDS . A B C D là

Lượt xem: 141,763 Cập nhật lúc: 18:33 18/01/2025

#8560 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh 3a\sqrt{3} a, SAS A vuông góc với mặt phẳng đáy và SA=2aS A = \sqrt{2} a. Góc giữa SCS C và mặt phẳng (ABCD)\left( A B C D \right) bằng

Lượt xem: 145,611 Cập nhật lúc: 23:00 18/01/2025

#8885 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh a2a \sqrt{2} và chiều cao bằng 2a2 a. Thể tích của khối chóp S.ABCDS . A B C D bằng:

Lượt xem: 151,131 Cập nhật lúc: 23:05 18/01/2025

#8302 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông cạnh a3a \sqrt{3}, cạnh bên SD=a6S D = a \sqrt{6} và SDS D vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SDS D và BCB C bằng

Lượt xem: 141,231 Cập nhật lúc: 23:13 18/01/2025

#7668 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy ABCDA B C D là hình vuông cạnh 2a2 a và SAS A vuông góc với đáy. Góc giữa SCS C và đáy bằng (45)@\left(45\right)^{@}. Thể tích khối chóp S.ABCDS . A B C D bằng.

Lượt xem: 130,396 Cập nhật lúc: 23:07 18/01/2025

#8376 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh aa, mặt bên SABS A B nằm trong mặt phẳng vuông góc với (ABCD)\left( A B C D \right), SAB^=(30)0\widehat{S A B} = \left(30\right)^{0}, SA=2aS A = 2 a. Tính thể tích VV của khối chóp S.ABCD.S . A B C D .

Lượt xem: 142,477 Cập nhật lúc: 23:05 18/01/2025

#7730 THPT Quốc giaToán

Cho hình chóp S.ABCDS . A B C D có đáy là hình vuông cạnh bằng 2\sqrt{2}, cạnh bên SAS A vuông góc với mặt đáy và SA=1S A = 1. Khoảng cách giữa hai đường thẳng SBS B và ACA C bằng

Lượt xem: 131,508 Cập nhật lúc: 23:44 16/01/2025


Đề thi chứa câu hỏi này:

58 . Đề thi thử TN THPT môn Toán năm 2024 - Chuyên Hùng Vương - Phú Thọ - Lần 2THPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,498 lượt xem 2,380 lượt làm bài