Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7903

Cho hình chóp tứ giác đều có cạnh đáy bằng aa và chiều cao bằng a62\dfrac{a \sqrt{6}}{2}. Góc giữa cạnh bên và mặt đáy bằng

A.  

90∘90 \circ

B.  

60∘60 \circ

C.  

45∘45 \circ

D.  

30∘30 \circ

Đáp án đúng là: B

(TH):
Phương pháp:
Hình chóp tứ giác đều là hình chóp có đáy là hình vuông, chân đường cao từ đỉnh trùng với tâm hình vuông Góc của đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
Cách giải:



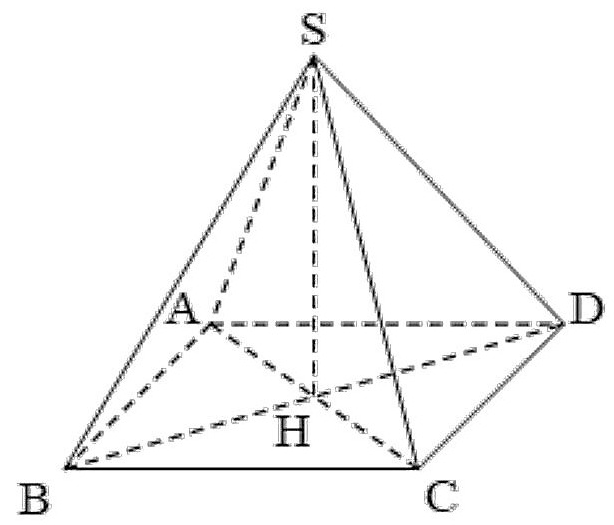
(SC,ABCD)=(SC,HC)=∠SCH\left( S C , A B C D \right) = \left( S C , H C \right) = \angle S C H
tanSCH=SHHC=a62a22=3⇒∠SCH=(60)@\text{tan} S C H = \dfrac{S H}{H C} = \dfrac{\dfrac{a \sqrt{6}}{2}}{\dfrac{a \sqrt{2}}{2}} = \sqrt{3} \Rightarrow \angle S C H = \left(60\right)^{@}


 

Câu hỏi tương tự:

#8247 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có cạnh đáy bằng aa (tham khảo hình vẽ bên). Khoảng cách từ BBđến mặt phẳng (SAC)\left( S A C \right) bằng

Lượt xem: 140,282 Cập nhật lúc: 13:52 16/01/2025

#8348 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có cạnh đáy bằng 2a,2 a , OO là tâm mặt đáy. Khoảng cách giữa hai đường thẳng SOS O và ABA B bằng

Lượt xem: 141,952 Cập nhật lúc: 08:25 17/01/2025

#8391 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, góc giữa cạnh bên và mặt đáy bằng 60°. Gọi M là trung điểm của SB. Thể tích hình chóp S.ACM bằng

Lượt xem: 142,686 Cập nhật lúc: 05:55 11/01/2025

#8167 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có đáy cạnh bằng aa, cạnh bên bằng a52\dfrac{a \sqrt{5}}{2}. Số góc đo giữa hai mặt phẳng (SAB)\left( S A B \right) và (ABCD)\left( A B C D \right) là

Lượt xem: 138,910 Cập nhật lúc: 23:39 18/01/2025

#11158 THPT Quốc giaToán

Cho hình chóp tam giác đều S.ABCS . A B C có cạnh đáy bằng 2a2 a và chiều cao bằng a2a \sqrt{2} (tham khảo hình vẽ dưới đây)



Khoảng cách từ điểm AA đến mặt phẳng (SBC)\left( S B C \right) bằng

Lượt xem: 189,716 Cập nhật lúc: 20:58 16/01/2025

#7824 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có đáy là hình vuông tâm OO cạnh 2a2 a và SO=a.S O = a . Khoảng cách từ OO đến mặt phẳng (SCD)\left( S C D \right) bằng

Lượt xem: 133,045 Cập nhật lúc: 23:18 18/01/2025

#7549 THPT Quốc giaToán

Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng aa. Một mặt phẳng thay đổi, vuông góc với SOS O và cắt SOS O, SAS A, SBS B, SCS C, SDS D lần lượt tại II, MM, NN, PP, QQ. Một hình trụ có một đáy là đường tròn ngoại tiếp tứ giác MNPQM N P Q và một đáy nằm trên mặt phẳng (ABCD)\left( A B C D \right). Thể tích khối trụ lớn nhất bằng

Lượt xem: 128,408 Cập nhật lúc: 19:38 18/01/2025

#8571 THPT Quốc giaToán

Cho hình chớp S.ABCS . A B C có đáy là tam giác đều cạnh a,SAa , S A vuông góc mặt phẳng đáy, SB=3aS B = \sqrt{3} a (tham khảo hình vẽ)



Khoảng cách từ trung điểm MM của SAS A đến mặt phẳng (SBC)\left( S B C \right) bằng

Lượt xem: 145,741 Cập nhật lúc: 08:22 17/01/2025

#8810 THPT Quốc giaToán

Cho hình chóp tứ giác đều S.ABCDS . A B C D có góc giữa mặt phẳng chứa mặt bên và mặt phẳng đáy bằng 60∘60 \circ. Biết rằng mặt cầu ngoại tiếp hình chóp S.ABCDS . A B C D có bán kính R=3.R = \sqrt{3} . Tính thể tích của khối chóp S.ABCS . A B C.

Lượt xem: 149,808 Cập nhật lúc: 23:17 18/01/2025


Đề thi chứa câu hỏi này:

15. Đề thi thử TN THPT môn Toán năm 2024 - THPT Tam Dương - Vĩnh Phúc.docxTHPT Quốc giaToán

1 mã đề 50 câu hỏi 1 giờ 30 phút

5,101 lượt xem 2,681 lượt làm bài