Trang chủ Hỏi & đáp THPT Quốc gia Toán Câu hỏi số #7808

Cho lăng trụ đứng ABC⋅A′B′C′A B C \cdot A^{'} B^{'} C^{'} có đáy là tam giác đều cạnh aa. Giả sử dd là một đường thẳng thay đổi luôn đi qua CC và dd không nằm trong các mặt phẳng (ABC)\left( A B C \right) và (ACC′A′)\left( A C C^{'} A^{'} \right). Gọi MNM N là đoạn vuông góc chung của hai đường thẳng AA′A A^{'} và d,Md , M thuộc đường thẳng dd và NN thuộc đường thẳng AA′A A^{'}. Giá trị nhỏ nhất của độ dài đoạn thẳng B′MB^{'} M là

A.  

a2\dfrac{a}{2}.

B.  

a33\dfrac{a \sqrt{3}}{3}.

C.  

a(3−1)2\dfrac{a \left( \sqrt{3} - 1 \right)}{2}.

D.  

a36\dfrac{a \sqrt{3}}{6}.

Đáp án đúng là: C

Lời giải



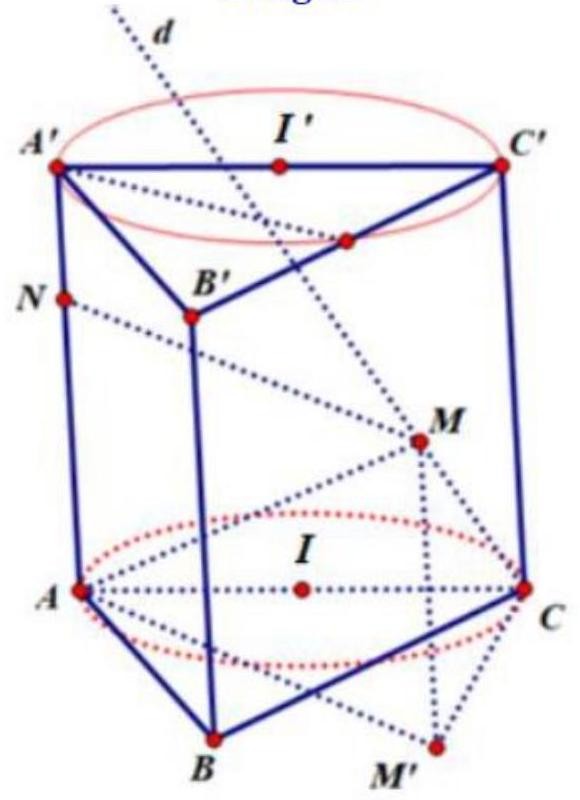
Giả sử MNM N là đoạn vuông góc chung của hai đường thẳng AA′A A^{'} và dd. Từ MM kẻ đường thẳng MM′∥AA′,M′∈(ABC)M M^{'} \parallel A A^{'} , M^{'} \in \left( A B C \right). Khi đó ta có AM′C=(90)@A M^{'} C = \left(90\right)^{@} nên luôn có M′M^{'} thuộc đường tròn đường kính ACA C nằm trong mặt phẳng (ABC)\left( A B C \right).
Gọi I,I′I , I^{'} lần lượt là trung điểm của AC,A′C′A C , A^{'} C^{'}, khi đó ta luôn có MM′∥II′M M^{'} \parallel I I^{'} và d(MM′;II′)=a2d \left( M M^{'} ; I I^{'} \right) = \dfrac{a}{2} do đó quỹ tích điểm MM là mặt trụ (T)\left( T \right) có trục là đường thẳng II′I I^{'}, bán kính đáy bằng a2\dfrac{a}{2}.
Khi đó mặt phẳng (A′B′C′)\left( A^{'} B^{'} C^{'} \right) cắt mặt trụ theo đường tròn đường kính A′C′A^{'} C^{'}. Vậy giá trị nhỏ nhất của BM′B M^{'} là: B′Mmin=B′I′−a2=a(3−1)2B^{'} M_{\text{min}} = B^{'} I^{'} - \dfrac{a}{2} = \dfrac{a \left( \sqrt{3} - 1 \right)}{2}.


 

Câu hỏi tương tự:

#8610 THPT Quốc giaToán

Cho lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy ABCA B C là tam giác vuông tại BB, AB=BC′=3aA B = B C^{'} = \sqrt{3} a, ACB^=60∘\hat{A C B} = 60 \circ. Lấy hai điểm M, NM , \textrm{ } N lần lượt trên hai cạnh AB′A B^{'} và A′CA^{'} C sao cho MB′→=2AM→,\overset{\rightarrow}{M B^{'}} = 2 \overset{\rightarrow}{A M} , A′C→=3A′N→\overset{\rightarrow}{A^{'} C} = 3 \overset{\rightarrow}{A^{'} N}. Thể tích khối đa diện BMNC′CB M N C^{'} C bằng

Lượt xem: 146,520 Cập nhật lúc: 07:14 26/04/2025

#7565 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là tam giác ABCA B C vuông cân tại AA, cạnh BC=a2B C = a \sqrt{2}. Góc giữa mặt phẳng (AB′C)\left( A B^{'} C \right) và mặt phẳng (BCC′B′)\left( B C C^{'} B^{'} \right) bằng 60∘60 \circ. Tính thể tích VV của khối đa diện AB′CA′C′A B^{'} C A^{'} C^{'}.

Lượt xem: 128,779 Cập nhật lúc: 06:19 26/04/2025

#8869 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là tam giác vuông cân tại BB, AB=aA B = a và A′B=a3A^{'} B = a \sqrt{3}. Thể tích khối lăng trụ ABC.A′B′C′A B C . A^{'} B^{'} C^{'} là

Lượt xem: 150,934 Cập nhật lúc: 13:36 23/04/2025

#8122 THPT Quốc giaToán

Cho khối lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là tam giác vuông cân tại BB, AB=AA′=1A B = A A^{'} = 1 (tham khảo hình vẽ).



Thể tích của khối lăng trụ đã cho bằng

Lượt xem: 138,252 Cập nhật lúc: 17:09 25/04/2025

#8459 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A ' B ' C ' có đáy ABCA B C là tam giác vuông tại BB, BC=aB C = a, mặt phẳng (A′BC)\left( A ' B C \right) tạo với đáy một góc 30∘30 \circ và tam giác A′BCA ' B C có diện tích bằng a23a^{2} \sqrt{3}. Tính thể tích khối lăng trụ ABC.A′B′C′A B C . A ' B ' C '.

Lượt xem: 143,911 Cập nhật lúc: 02:51 23/04/2025

#8071 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy là một tam giác vuông cân tại BB. AB=AA′=2a,A B = A A^{'} = 2 a , M,NM , N lần lượt là trung điểm của BCB Cvà BB′B B^{'}. Khoảng cách giữa hai đường thẳng MNM N và AC′A C^{'} bằng

Lượt xem: 137,289 Cập nhật lúc: 05:59 26/04/2025

#8941 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy ABC là tam giác vuông tại B với AB=2a,  BC=aA B = 2 a , \textrm{ }\textrm{ } B C = a và AA′=4a.A A^{'} = 4 a . Gọi M là trung điểm của cạnh AB.A B . Khoảng cách giữa hai đường thẳng AB′A B^{'} và CM bằng

Lượt xem: 152,091 Cập nhật lúc: 05:51 26/04/2025

#8557 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A ' B ' C ', có đáy ABCA B Clà tam giác vuông cân tại A,AA′=aA , A A ' = a, A′B=a5A ' B = a \sqrt{5}. Thể tích khối lăng trụ ABC.A′B′C′A B C . A ' B ' C 'là

Lượt xem: 145,630 Cập nhật lúc: 16:45 25/04/2025

#7537 THPT Quốc giaToán

Cho hình lăng trụ đứng ABC.A′B′C′A B C . A^{'} B^{'} C^{'} có đáy ABCA B C tam giác vuông cân tại A,AB=a,AA′=a2.A , A B = a , A A^{'} = a \sqrt{2} . Gọi MM là trung điểm BC.B C . Khoảng cách giữa hai đường thẳng AMA M và B′CB^{'} C bằng

Lượt xem: 128,209 Cập nhật lúc: 06:10 26/04/2025


Đề thi chứa câu hỏi này:

50. Đề thi thử TN THPT môn Toán năm 2024 - SỞ GIÁO DỤC NINH BÌNH - LẦN 2

1 mã đề 50 câu hỏi 1 giờ 30 phút

4,623 xem348 thi