Cho
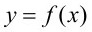
là hàm số bậc ba có đồ thị như hình vẽ bên dưới
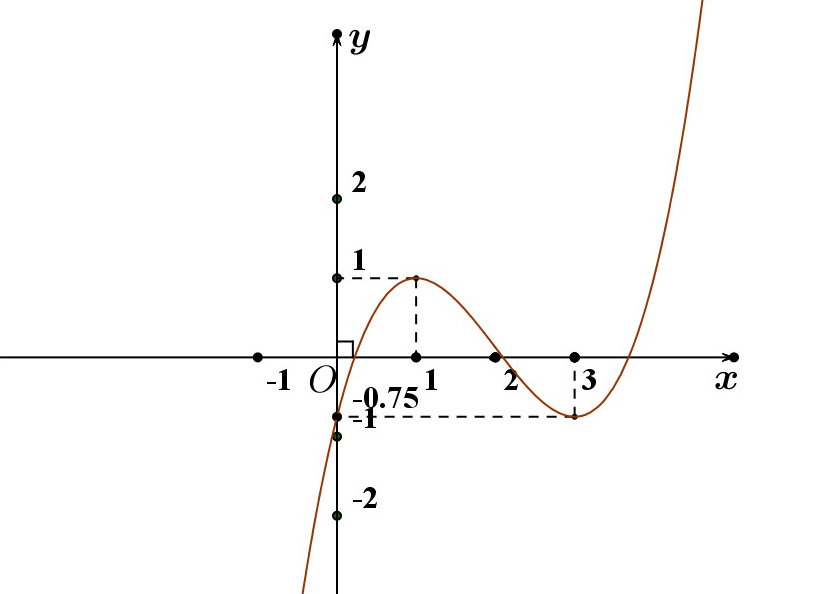
Hàm số
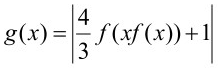
có bao nhiêu điểm cực trị?
A.
B.
C.
D.
Đáp án đúng là: A
Cho
![]()

Hàm số
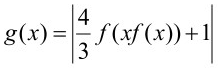
Đáp án đúng là: A
Cho
![]()
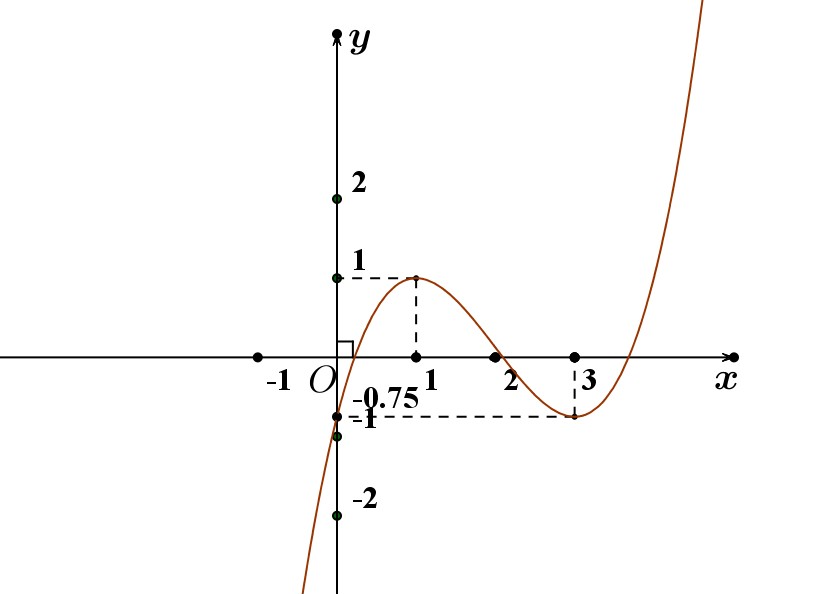
Hàm số
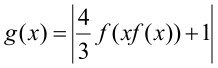
A. B. C. D.
Lời giải
Đặt
Khi đó .
Từ đồ thị ta được hàm số
+ có 3 nghiệm phân biệt khác 0 (do đồ thị hàm số
![]()
+ Phương trình nếu có nghiệm là nghiệm bội chẵn.
Suy ra phương trình
![]()
Xét
(1)
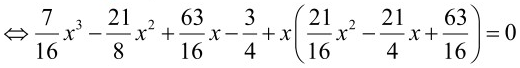
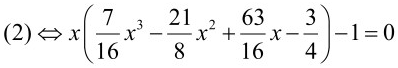
(3)
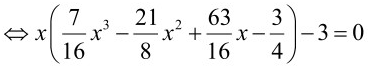
Các nghiệm của (1), (2) và (3) đều đôi một khác nhau.
Suy ra phương trình
![]()
![]()
Do đó hàm số
![]()
![]()
Câu hỏi tương tự:
#3909 THPT Quốc giaVật lý
Cho mạch điện trong đó ống dây thuần cảm có độ tự cảm L, điện trở thuần R thay đổi được, tụ điện có điện dung C, các vôn kế nhiệt lý tưởng. Khi đặt vào hai đầu của mạch một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi, rồi thay đổi R ta thấy số chỉ vôn kế luôn không đổi bằng . Khi điều chỉnh thì vôn kế chỉ 240 V và mạch tiêu thụ công suất bằng
Lượt xem: 66,592 Cập nhật lúc: 19:44 25/04/2025
#1606 THPT Quốc giaVật lý
Lượt xem: 27,413 Cập nhật lúc: 19:35 25/04/2025
#8808 THPT Quốc giaToán
Cho mặt cầu có bán kính bằng 4, hình trụ có chiều cao bằng 4 và hai đường tròn đáy nằm trên . Gọi là thể tích khối trụ và là thể tích của khối cầu . Tỉ số bằng
Lượt xem: 149,893 Cập nhật lúc: 02:07 23/04/2025
#11539 THPT Quốc giaSinh học
Cho biết các công đoạn được tiến hành trong chọn giống như sau:
(1) Chọn lọc các tổ hợp gen mong muốn.
(2) Tạo dòng thuần chủng có các kiểu gen khác nhau.
(3) Lai các dòng thuần chủng với nhau.
(4) Tạo dòng thuần chủng có kiểu gen mong muốn.
Việc tạo giống thuần dựa trên nguồn biến dị tổ hợp được thực hiện theo quy trình:
Lượt xem: 196,284 Cập nhật lúc: 16:25 24/04/2025
#8935 THPT Quốc giaToán
Cho hàm số
liên tục trên
có bảng xét dấu
Số điểm cực đại của hàm số đã cho là:
Lượt xem: 152,065 Cập nhật lúc: 16:16 25/04/2025
#7857 THPT Quốc giaToán
Cho khối trụ có bán kính đáy bằng và chiều cao . Thể tích của khối trụ đã cho bằng
Lượt xem: 133,638 Cập nhật lúc: 07:05 25/04/2025
#2737 THPT Quốc giaVật lý
Cho dòng điện không đổi cường độ chạy qua một ống dây dài , gồm 400 vòng dây. Cảm ứng từ tạo ra trong lòng ống dây có độ lớn xấp xỉ bằng
Lượt xem: 46,611 Cập nhật lúc: 18:56 25/04/2025
#8426 THPT Quốc giaToán
Cho hình trụ có hai đáy là hai hình tròn và , thiết diện qua trục của hình trụ là hình vuông. Gọi và là hai điểm lần lượt nằm trên hai đường tròn và . Biết và khoảng cách giữa và bằng . Bán kính đáy của hình trụ bằng
Lượt xem: 143,343 Cập nhật lúc: 18:37 25/04/2025
#1860 THPT Quốc giaVật lý
Cho đoạn mạch nối tiếp như hình bên. Đặt vào AB một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Điều chỉnh R đến giá trị thì công suất tiêu thụ trên biến trở đạt cực đại, khi đó tỉ số hệ số công suất của đoạn mạch AB và đoạn mạch MB là . Giá trị điện trở r của cuộn dây bằng
Lượt xem: 31,779 Cập nhật lúc: 07:03 26/04/2025
#4293 THPT Quốc giaVật lý
Cho mạch điện RLC nối tiếp. Trong đó . Điện áp xoay chiều đặt vào hai đầu đoạn mạch không đổi . Để u và i cùng pha, người ta ghép thêm với C một tụ điện có điện dung , giá trị và cách ghép C với là
Lượt xem: 73,152 Cập nhật lúc: 16:49 25/04/2025
Đề thi chứa câu hỏi này:
1 mã đề 50 câu hỏi 1 giờ 30 phút
576 xem32 thi
